Глава 5

Элементы специальной теории относительности

§ 5.1. Механический принцип относительности. Преобразования Галилея

Механический принцип относительности утверждает, что законы динамики одинаковы во всех инерциальных системах отсчета.

Система движется относительно инерциальной системыК равномерно и прямолинейно со скоростью (). Скорость направлена вдольO. Тогда =t. Преобразования координат Галилея Задают связь между радиусами-векторами или координатами произвольной точки A в обеих системах:

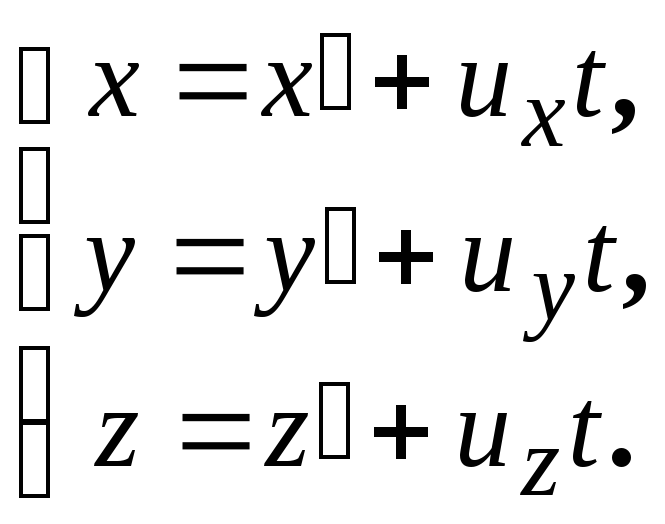=или(5.1)

Правило сложения скоростей в классической механике

Продифференцировав равенство по времени и учитывая, что вклассической механике , получаем

(5.2)

Продифференцировав (5.2) по времени, получим соотношение для ускорений:

.

Таким образом, имеем

(5.3)

т.е. система инерциальна (точкаAдвижется относительно ее равномерно).

Это и есть доказательство механического принципа относительности.

Записанные соотношения (5.1)–(5.3) справедливы лишь в классической механике ( c), где с – скорость света в вакууме м/с.

§ 5.2. Постулаты специальной теории относительности (сто). Преобразования Лоренца Постулаты Эйнштейна

I. Принцип относительности:никакие опыты (механические, электрические, оптические), проведенные внутри данной инерциальной системы отсчета, не дают возможность обнаружить, покоится ли эта система или движется равномерно и прямолинейно;все законы природы инвариантны (неизменны) по отношению к переходу от одной инерциальной системы отсчета к другой.

II. Принцип инвариантности скорости света: скорость света в вакууме не зависит от скорости движения источника света или наблюдателя иодинакова во всех инерциальных системах отсчета.

Первый постулат Эйнштейна, являясь обобщением механического принципа относительности Галилея на любые физические процессы, утверждает, таким образом, что физические законы инвариантны по отношению к выбору инерциальной системы отсчета. Согласно этому постулату, все инерциальные системы отсчета совершенно равноправны. Согласно второму постулату Эйнштейна ,постоянство скорости света — фундаментальное свойство природы, которое констатируется как опытный факт.

Преобразования Лоренца (при )

Система движется относительно системыKсо скоростьювдоль осиX (рис.5.2.).

Преобразования Лоренца имеют следующий вид:

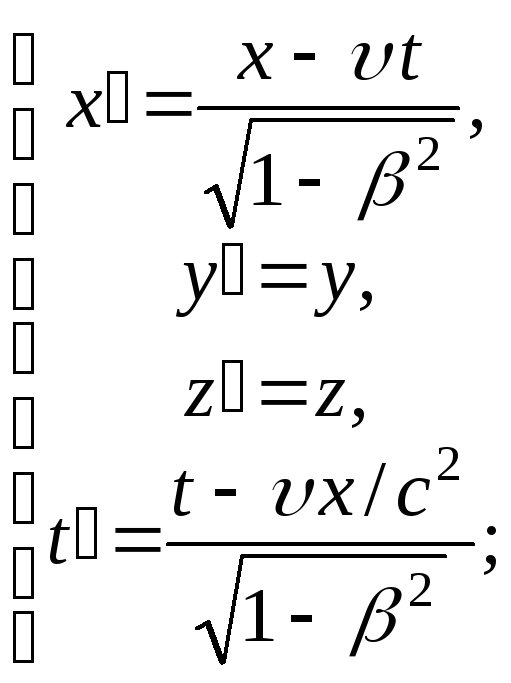
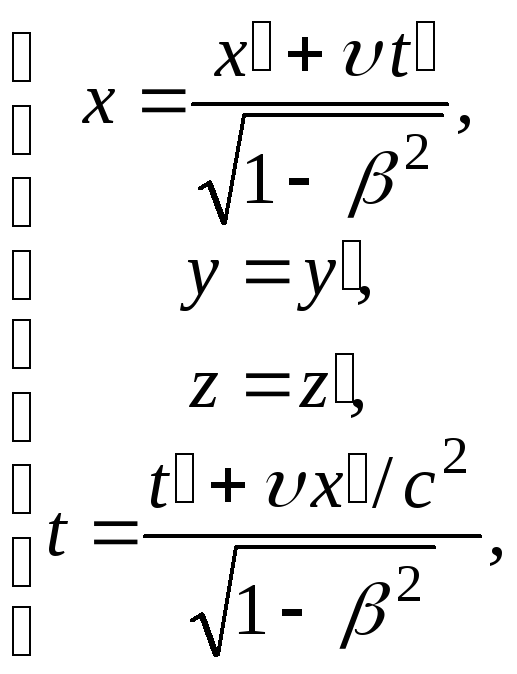(5.4)

где .

1. Эти уравнения симметричны и отличаются лишь знаком при .

2. При они переходят в классические преобразования Галилея (5.1).

3) В закон преобразования координат входит время, а в закон преобразования времени — пространственные координаты (устанавливается взаимосвязь пространства и времени).

§ 5.3. Следствия из преобразований Лоренца

Относительность одновременности

Пусть в системев точках с координатамиив моменты времениипроисходят два события. В системеим соответствуют координатыии моментыи. Если события в системепроисходят в одной точке () и являются одновременными (), то, согласно преобразованиям Лоренца (5.4)

,, (5.5)

т.е. эти события являются одновременными и пространственно совпадающими для любой инерциальной системы отсчета.

Если события в системе пространственно разобщены (), но одновременны (), то в системе, согласно преобразованиям Лоренца (5.4)

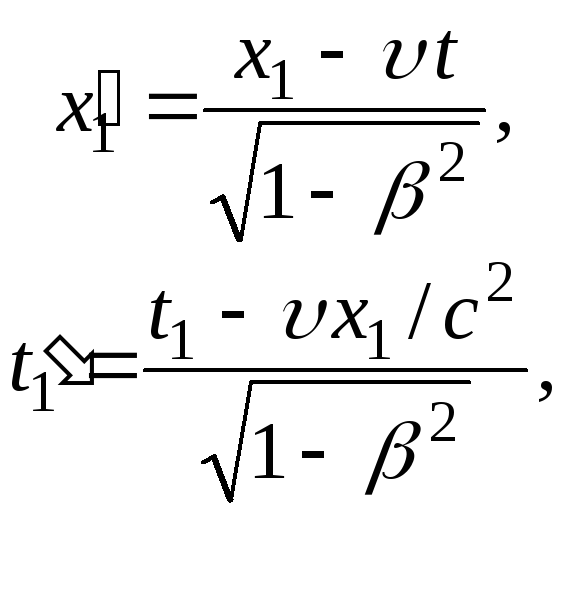
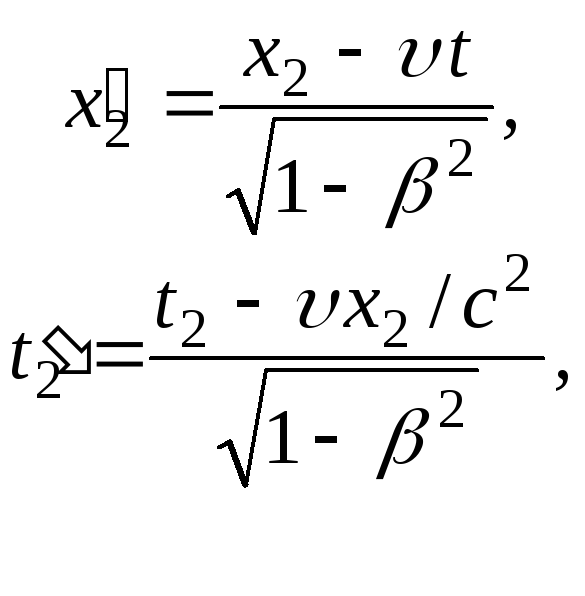(5.6)

Из (5.6) следует, что и. Таким образом, в системеэти события,оставаясь пространственно разобщенными, оказываются и неодновременными.

Длительность событий в разных системах отсчета

Пусть в некоторой точке (с координатой), покоящейся относительно системыK, происходит событие, длительность которого (разность показаний часов в конце и начале события), где индексы 1 и 2 соответствуют началу и концу события. Длительность этого же события в системе

, (5.7)

где

,. (5.8)

Подставив (5.8) в (5.7), получаем

, или

. (5.9)

Отметим, что , т.е.длительность события, происходящего в некоторой точке, наименьшая в той инерциальной системе отсчета, относительно которой эта точка неподвижна. Следовательно, часы, движущиеся относительно инерциальной системы отсчета, идут медленнее покоящихся часов, т.е. ход часов замедляется в системе отсчета, относительно которой часы движутся.

Длина тел в разных системах отсчета

Рассмотрим стержень, расположенный вдоль оси и покоящийся относительно системы. Длина стержня в системе будет , гдеи– не изменяющиеся со временемкоординаты начала и конца стержня, индекс ноль показывает, что в системестержень покоится. Определим длину этого стержня в системеK, относительно которой он движется со скоростью .

Для этого необходимо измерить координаты его концов ив системеKв один и тот же момент времени t. Их разностьи даст длину стержня в системеK:

, (5.10)

т.е.

. (5.11)

Размер тела, движущегося относительно инерциальной системы отсчета, уменьшается в направлении движении в раз, т.е. лоренцево сокращение длины тем больше, чем больше скорость движения.При этом поперечные размеры тела не зависят от скорости его движения и одинаковы во всех инерциальных системах отсчета.

Релятивистский закон сложения скоростей

Пусть материальная точка движется в системе вдоль оси, адвижется относительноKсо скоростью(осиx исовпадают), тогда из (5.4) получим

(5.12)

(5.13)

Подставляя (5.13) в (5.12), получим релятивистский закон сложения скоростей:

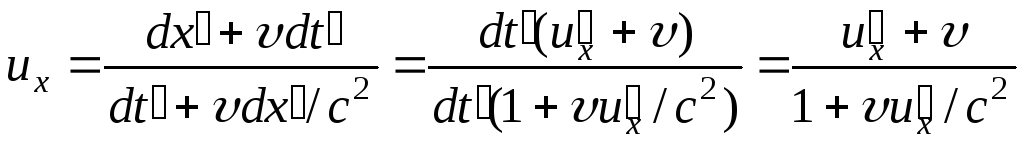. (5.14)

Аналогично получим обратные преобразования

. (5.15)

Если скорости малы по сравнению со скоростью светаc, то эти формулы переходят в закон сложения скоростей в классической механике. Релятивистский закон сложения скоростейне противоречит второму постулату Эйнштейна.В самом деле, если, то. Если, то, т.е. скоростьс – предельная скорость, которую невозможно превысить.