Глава 7
Волны
§ 7.1. Волновые процессы. Механизм образования механических волн в упругой среде
Один из самых простых способов продемонстрировать волновое движение – это взять свободный конец длинной веревки, второй конец которой закреплен, и дернуть его вверх и вниз. Вдоль веревки побегут горбы и впадины волн, и если бы веревка была бесконечно длинной, то такие волны можно было бы назвать бегущими волнами – так называются волны, распространяющиеся в неограниченной среде, где нет отражения (рис.7.1.)
Если размеры среды ограничены, например если веревку заменить скрипичной струной с закрепленными обоими концами, то бегущие волны, распространяющиеся по струне, отражались бы от обоих концов. Тогда колебания струны представляли бы собой комбинацию таких волн, распространяющихся взад и вперед по струне, и образовались бы стоячие волны.

Процесс распространения колебаний в пространстве называется волной. Частицы среды, в которой распространяется волна, не вовлекаются волной в поступательное движение, они лишь совершают колебания около своих положений равновесия. В зависимости от направления колебаний частиц по отношению к направлению, в котором распространяется волна, различают продольныеипоперечныеволны. В продольной волне частицы среды колеблются вдоль направления распространения волны. Упругие поперечные волны могут возникнуть лишь в среде, обладающей сопротивлением сдвигу. Поэтому в жидкой и газообразной средах возможно возникновение только продольных волн. В твердой среде возможно возникновение как продольных так и поперечных волн.
Геометрическое место точек до которых доходят колебания к моменту времени t,называетсяфронтом волны(иливолновым фронтом). Фронт волны представляет собой ту поверхность, которая отделяет часть пространства, уже вовлеченную в волновой процесс, от области в которой колебания еще не возникли.
Геометрическое место точек, колеблющихся в одинаковой фазе, называетсяволновой поверхностью.
Волновых поверхностей существует бесконечное множество, в то время как волновой фронт каждый момент времени только один. Волновые поверхности могут быть любой формы. В простейших случаях они имеют форму плоскости или сферы. Соответственно волна в этих случаях называется плоской илисферической.
Плоскими волнами называются волны, поверхности одинаковой фазы которых представляют собой плоскости.
Сферическими волнами называются волны, поверхности одинаковой фазы которых представляют собой сферы.
|
|
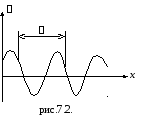
Пусть плоская волна распространяется вдоль оси x. Тогда все точки среды, положения равновесия которых имеют одинаковую координатуx(но различные значения координатy и z), колеблются в одинаковой фазе. На рис.7.2. изображена кривая, которая дает смещениеΨиз положения равновесия точек с различнымиxв некоторый момент времени. |
Расстояние , на которое распространяется волна за время, равное периоду колебаний частиц среды, называется длиной волны.
Очевидно, что
![]() , (7.1)
, (7.1)
где – скорость волны,T – период колебаний.
Длину волны можно определить также как расстояние между ближайшими точками среды, колеблющимися с разностью фаз, равной 2π(рис.7.2.).
Заменив в соотношении (7.1) Tчерез 1/v(v – частота колебаний), получим
![]() , (7.2)
, (7.2)
При волновом движении существует три скорости, которые представляют собой совершенно различные величины, хотя они и связаны математически.
Скорость частиц. Это скорость простых гармонических колебаний частиц среды около их положений равновесия.
Волновая, или фазовая скорость. Это скорость с которой перемещается в среде поверхности одинаковой фазы, т.е. горбы или впадины.
Групповая скорость. Путем сложения ряда волн с разными частотами (длинами волн) и скоростями можно получить группу волн, или волновой пакет. Волны редко существуют в виде отдельных монохроматических компонент. Импульс белого света имеет сплошной спектр частот, поэтому движение такого импульса описывается его групповой скоростью. Конечно, такой пакет расплывается со временем, поскольку волновые скорости каждой компоненты неодинаковы во всех средах, кроме свободного пространства. Только в свободном пространстве импульс белого света остается неизменным.
Мы рассмотрим вопрос о групповой скорости отдельно в одном из последующих разделов данной главы. Групповая скорость имеет важное значение как скорость, с которой переносится энергия в волновой группе. В случае монохроматической волны групповая и волновая скорости одинаковы.