
ТАУ - Пр 3
.docxМинистерство образования науки Российской Федерации
Тольяттинский государственный университет
Кафедра «Электроснабжение и электротехника»
Практическая работа №3
«Критерий устойчивости Гурвица»
по дисциплине «Теория автоматического управления»
Выполнил: Назаров М.А.
Осипов А.Д.
Цветков Е.Д.
Проверил: Денисов В.А.
Тольятти, 2017
-
Цель работы
Определить устойчивость замкнутой системы.
-
Ход работы
Заданная функция имеет вид:
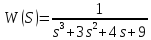
Определим устойчивость путем вычисления полюсов замкнутой системы в программе Matlab.
Зададим скрипт:
H=tf([1],[1 3 4 9])
pole(H)
pzmap(H)
На рисунке 1 представлены значения полюсов системы на координатной плоскости.
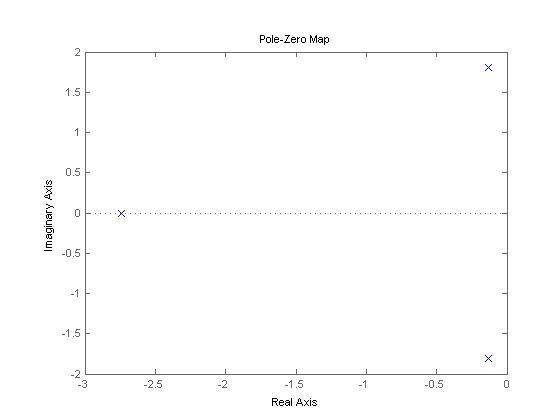
Рисунок 1 – График значений полюсов системы
Все корни расположены в левой полуплоскости, значит, система устойчива.
Найдем определитель матрицы:
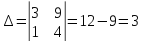
Поскольку
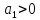 ,
,
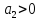 ,
,
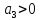 ,
,
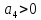 ,
а
,
а
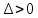 ,
то система устойчива.
,
то система устойчива.
Запишем скрипт в Matlab:
A=[3 9 0;1 4 0; 0 3 9]
p=poly(A)
roots(p)
Результаты вычислений представлены на рисунке 2.
Так как система при вычислении имеет комплексные корни, которые находятся в левой части плоскости, то система устойчива.
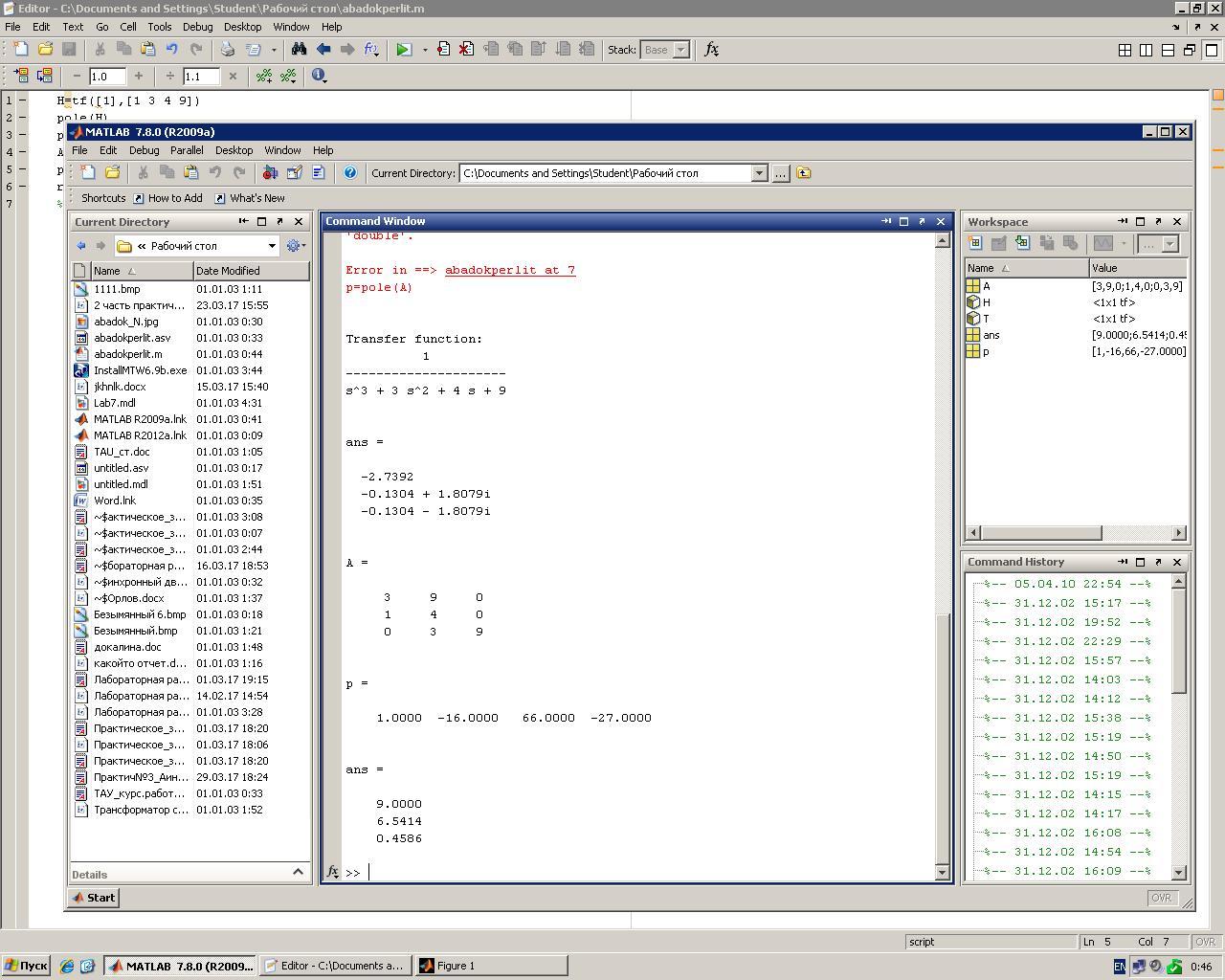
Рисунок 2 – Результаты определения устойчивости замкнутой системы по критерию Гурвица
Вывод
В ходе выполнения лабораторной работы исследовали устойчивость замкнутой системы по двум критериям:
-
по расположению полюсов замкнутой системы на плоскости;
-
по критерию Гурвица.
Замкнутая система с передаточной характеристикой оказалась устойчивой по каждому из критериев.
