
- •Задача 1. Обработка результатов наблюдений
- •Построить вариационный (статистический) ряд:
- •Построить для полученного вариационного ряда гистограмму и эмпирическую функцию распределения:
- •Оценить точность выборки.
- •Проверить согласованность теоретического и статистического распределений, используя критерий Пирсона.
- •Задача 2. Статистический анализ связей
- •Список использованной литературы:
Проверить согласованность теоретического и статистического распределений, используя критерий Пирсона.
Критерий Пирсона
основан на сравнении эмпирических и
теоретических частот. Для его использования
необходимо, чтобы в каждом интервале
группировки было достаточное количество
данных. В случае малочисленных эмпирических
частот (niэмп<
5) следует объединить соседние интервалы,
в этом случае и соответствующие им
теоретические частоты также складываются.
При этом необходимо следить за
правильностью расчета значений функции
нормального распределения, теоретических
частот и выполнением условия
 .
.
Объединим первый
и второй интервалы, частота для
объединенного интервала будет 6+14=20.
Объединим восьмой и девятый интервалы,
частота для объединенного последнего
интервала 2+2=4. Общее количество интервалов
группировки после объединения m=7.
Дополним скорректированную таблицу
столбцом «мера расхождения», выполнив
расчеты по формуле Пирсона
 .
.
|
ai |
bi |
xi |
ni |
Ф(х) |
ni теор |
хи2 i |
|
|
|
|
|
|
|
|
|
0,2 |
4,2 |
2,2 |
20 |
0,154072 |
15,40716 |
1,369112 |
|
4,2 |
6,2 |
5,2 |
12 |
0,322178 |
16,81063 |
1,376639 |
|
6,2 |
8,2 |
7,2 |
23 |
0,538197 |
21,60187 |
0,090491 |
|
8,2 |
10,2 |
9,2 |
19 |
0,743251 |
20,50542 |
0,110521 |
|
10,2 |
12,2 |
11,2 |
17 |
0,887035 |
14,3784 |
0,477994 |
|
12,2 |
14,2 |
13,2 |
5 |
0,961504 |
7,446962 |
0,804036 |
|
14,2 |
18,2 |
16,2 |
4 |
0,998033 |
3,652877 |
0,032986 |
|
суммы |
|
|
100 |
|
100 |
4,26178 |
Фактически наблюдаемое значение статистики Пирсона составляет
 =4,26.
=4,26.
Критическое
значение статистики
 = 9,48 найдено для уровня значимости 5% и
числа степеней свободы k=m-3=4
с помощью функции ХИ2ОБР.
= 9,48 найдено для уровня значимости 5% и
числа степеней свободы k=m-3=4
с помощью функции ХИ2ОБР.
Сравним фактическое
значение статистики
 с критической величиной
с критической величиной
 и сделаем вывод в соответствии со схемой:
и сделаем вывод в соответствии со схемой:

 теоретическое
и статистическое распределения
согласованы, на уровне значимости
теоретическое
и статистическое распределения
согласованы, на уровне значимости
 следует принять гипотезу о нормальном
законе распределения случайной величины
Х
– стажа работ.
следует принять гипотезу о нормальном
законе распределения случайной величины
Х
– стажа работ.
Задача 2. Статистический анализ связей
Исходными данными для моделирования являются социально-экономические показатели субъектов Сибирского федерального округа (Приложение 1). Требуется исследовать зависимость результирующего признака Y, соответствующего варианту задания, от факторных переменных Х1, Х2 и Х3:
-
Рассчитать матрицу парных коэффициентов корреляции; проанализировать тесноту и направление связи результирующего признака Y с каждым из факторов Х; оценить статистическую значимость коэффициентов корреляции r(Y, Xi); выбрать наиболее информативный фактор.
-
Построить модель парной регрессии с наиболее информативным фактором; дать экономическую интерпретацию коэффициента регрессии.
-
Проверить значимость коэффициентов модели с помощью t–критерия Стьюдента (принять уровень значимости α=0,05).
-
Оценить качество модели с помощью средней относительной ошибки аппроксимации, коэффициента детерминации и F – критерия Фишера (принять уровень значимости α=0,05).
-
С доверительной вероятностью γ=80% осуществить прогнозирование среднего значения показателя Y (прогнозные значения факторов приведены в Приложении 1). Представить графически фактические и модельные значения Y, результаты прогнозирования.
|
7 |
Y7 |
Потребление хлебных продуктов на душу населения (в год), кг |
|
Сибирский федеральный округ |
Х1 |
Х2 |
Х3 |
Y1 |
Y2 |
Y3 |
Y4 |
Y5 |
Y6 |
Y7 |
Y8 |
Y9 |
Y10 |
|
Республика Алтай |
13836,9 |
15632,4 |
106,4 |
7179,0 |
1,7 |
0,7 |
16,4 |
38,4 |
183,2 |
143 |
275 |
87 |
37 |
|
Республика Бурятия |
15715,5 |
19924,0 |
107,5 |
11340,0 |
1,2 |
2,1 |
23,2 |
14,9 |
191,7 |
117 |
262 |
65 |
30 |
|
Республика Тыва |
10962,8 |
19163,1 |
107,3 |
4944,6 |
1,7 |
0,1 |
21,1 |
42,8 |
135,4 |
135 |
178 |
40 |
25 |
|
Республика Хакасия |
14222,8 |
20689,5 |
107,6 |
9680,5 |
1,3 |
1,3 |
25,0 |
19,3 |
247,7 |
134 |
263 |
110 |
31 |
|
Алтайский край |
12499,9 |
13822,6 |
104,8 |
9765,7 |
2,3 |
1,4 |
20,8 |
10,3 |
229,6 |
168 |
334 |
102 |
40 |
|
Забайкальский край |
15968,8 |
21099,6 |
107,8 |
10572,7 |
1,8 |
0,4 |
23,3 |
22,0 |
218,2 |
116 |
246 |
88 |
33 |
|
Красноярский край |
20145,5 |
25658,6 |
106,1 |
14105,7 |
1,8 |
3,8 |
29,7 |
13,3 |
262,1 |
117 |
242 |
118 |
27 |
|
Иркутская область |
16017,2 |
22647,7 |
107,4 |
10580,2 |
1,3 |
1,9 |
22,5 |
19,0 |
224,3 |
113 |
198 |
82 |
34 |
|
Кемеровская область |
16666,0 |
20478,8 |
106,5 |
11237,2 |
1,7 |
2,4 |
26,3 |
18,9 |
210,1 |
130 |
228 |
77 |
34 |
|
Новосибирская область |
18244,1 |
20308,5 |
106,2 |
14898,1 |
2,1 |
2,4 |
21,7 |
5,1 |
260,2 |
125 |
289 |
127 |
35 |
|
Омская область |
17247,9 |
19087,8 |
105,0 |
12663,1 |
1,7 |
2,3 |
25,1 |
15,8 |
223,5 |
138 |
343 |
132 |
47 |
|
Томская область |
16516,0 |
24001,0 |
106,1 |
11199,4 |
1,5 |
3,3 |
24,5 |
16,0 |
231,3 |
120 |
263 |
95 |
34 |
|
Прогнозные значения |
16500,0 |
21000,0 |
106,0 |
|
|
|
|
|
|
|
|
|
|
Решение:
Рассчитать матрицу парных коэффициентов корреляции; проанализировать тесноту и направление связи результирующего признака Y с каждым из факторов Х; оценить статистическую значимость коэффициентов корреляции r(Y, Xi); выбрать наиболее информативный фактор.
Используем Excel (Данные / Анализ данных / КОРРЕЛЯЦИЯ):

Получим матрицу коэффициентов парной корреляции между всеми имеющимися переменными:

Проанализируем коэффициенты корреляции между результирующим признаком Y и каждым из факторов Xj:
r (Y,X1)=-0,58<0, следовательно, между переменными Y и Х1 наблюдается обратная корреляционная зависимость: потребление хлебных продуктов на душу населения (в год), ниже для среднедушевых денежных доходов (в месяц).
r (Y,X2)=-0,85<0, значит, между переменными Y и Х2 наблюдается обратная корреляционная зависимость: потребление хлебных продуктов на душу населения (в год), ниже чем среднемесячная номинальная начисленная заработная плата работников организаций.
r (Y,X3)=-0,61<0, значит, между переменными Y и Х3 наблюдается обратная корреляционная зависимость: потребление хлебных продуктов на душу населения (в год), ниже чем индекс потребительских цен (декабрь к декабрю предыдущего года).
Для проверки значимости найденных коэффициентов корреляции используем критерий Стьюдента.
Для
каждого коэффициента корреляции
 вычислим t-статистику
по формуле
вычислим t-статистику
по формуле
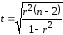 и занесем результаты расчетов в
дополнительный столбец корреляционной
таблицы:
и занесем результаты расчетов в
дополнительный столбец корреляционной
таблицы:
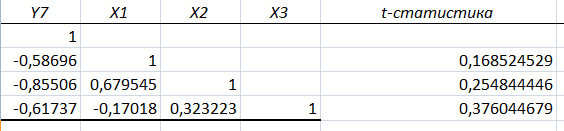
По таблице
критических точек распределения
Стъюдента при уровне значимости
 и числе степеней свободы k=n-2=12-2=10,
определим критическое значение tкр.=2,22
(функция СТЬЮДРАСПОБР).
и числе степеней свободы k=n-2=12-2=10,
определим критическое значение tкр.=2,22
(функция СТЬЮДРАСПОБР).
Сопоставим фактические значения t с критическим tkp, и сделаем выводы в соответствии со схемой:
![]()
t
(r(Y,X1))=0,16<tкр.=2,22
, следовательно,
коэффициент
 не является значимым.
не является значимым.
t
(r(Y,X2))=0,25<tкр.=2,22,
следовательно, коэффициент
 не является значимым.
не является значимым.
t
(r(Y,X3))=0,37<tкр.=2,22,
следовательно, коэффициент
 не является значимым.
не является значимым.
Построить модель парной регрессии с наиболее информативным фактором; дать экономическую интерпретацию коэффициента регрессии.
Для построения
парной линейной модели
 используем программу РЕГРЕССИЯ (Данные
/ Анализ данных). В качестве «входного
интервала Х»
покажем значения фактора Х1.
используем программу РЕГРЕССИЯ (Данные
/ Анализ данных). В качестве «входного
интервала Х»
покажем значения фактора Х1.
Результаты вычислений представлены в таблицах:



Коэффициенты модели содержатся в третьей таблице итогов РЕГРЕССИИ (столбец Коэффициенты).
Таким образом, модель парной регрессии построена, ее уравнение имеет вид
YT=186, 93*X1
Проверить значимость коэффициентов модели с помощью t–критерия Стьюдента (принять уровень значимости α=0,05).
Значимость коэффициентов модели проверим с помощью t – критерия Стьюдента.
t – статистики для коэффициентов уравнения регрессии приведены в столбце «t–статистика» третьей таблицы итогов РЕГРЕССИИ:
-
для свободного коэффициента a=186,93 определена статистика t(a)=7,3.
-
для коэффициента регрессии b=0 определена статистика t(b)=-2,2.
Критическое значение tкр=2,22 найдено для уровня значимости =5% и числа степеней свободы 10 (функция СТЬЮДРАСПОБР).
Схема проверки:
![]()
t (a)=7,3>tкр. свободный коэффициент а является значимым.
t(b)=2,29>tкр. коэффициент регрессии b является значимым.
Выводы о значимости коэффициентов модели сделаны на уровне значимости =5%. Рассматривая столбец «Р-значение», отметим, что свободный коэффициент а можно считать значимым на уровне 2,32Е-05; коэффициент регрессии b – на уровне 0,04.
Оценить качество модели с помощью средней относительной ошибки аппроксимации, коэффициента детерминации и F – критерия Фишера (принять уровень значимости α=0,05).
Для вычисления
средней
относительной ошибки аппроксимации
рассмотрим остатки модели
 ,
содержащиеся в столбце Остатки
итогов программы РЕГРЕССИЯ (таблица
«Вывод
остатка»).
Дополним таблицу столбцом относительных
погрешностей, которые вычислим по
формуле
,
содержащиеся в столбце Остатки
итогов программы РЕГРЕССИЯ (таблица
«Вывод
остатка»).
Дополним таблицу столбцом относительных
погрешностей, которые вычислим по
формуле
 с помощью функции ABS.
с помощью функции ABS.

По столбцу относительных погрешностей найдем среднее значение Eотн=7,57 (функция СРЗНАЧ).
Оценим точность построенной модели в соответствии со схемой:
![]()
Eотн=7,57 – модель имеет удовлетворительную точность.
Коэффициент детерминации R-квадрат определен программой РЕГРЕССИЯ (таблица «Регрессионная статистика») и составляет R2=0,34. Таким образом, вариация (изменение) потребления хлебных продуктов Y на 34% объясняется по уравнению модели вариацией среднедушевых доходов.
Проверим значимость полученного уравнения с помощью F – критерия Фишера.
F – статистика определена программой РЕГРЕССИЯ (таблица «Дисперсионный анализ») и составляет F = 5,25.
Критическое значение Fкр= 4,96 найдено для уровня значимости =5% и чисел степеней свободы k1=1, k2=12 (функция FРАСПОБР).
Схема проверки:
![]()
Сравнение показывает: F = 5,25 > Fкр = 4,96; следовательно, уравнение модели является значимым, его использование целесообразно, зависимая переменная Y (потребление хлебных продуктов) достаточно хорошо описывается включенной в модель факторной переменной Х1 (среднедушевые доходы в месяц).
С доверительной вероятностью γ=80% осуществить прогнозирование среднего значения показателя Y (прогнозные значения факторов приведены в Приложении 1). Представить графически фактические и модельные значения Y, результаты прогнозирования.
Согласно условию задачи прогнозное значение факторной переменной Х1 составляет 16500,0. Рассчитаем по уравнению модели прогнозное значение показателя Y:
YT=186.93*16500=3084840
Таким образом, если среднедушевые доходы составят 16500, то потребление хлебных продуктов будет около 308 кг.
Зададим доверительную
вероятность
 и построим доверительный
прогнозный интервал для среднего
значения Y.
и построим доверительный
прогнозный интервал для среднего
значения Y.
Для этого нужно рассчитать стандартную ошибку прогнозирования для среднего значения результирующего признака
 .
.
Предварительно подготовим:
-
стандартную ошибку модели SE=13,2 (таблица «Регрессионная статистика» итогов РЕГРЕССИИ);
по столбцу исходных данных Х1 найдем среднее значение равное 15670 (функция СРЗНАЧ) и определим ∑(xi-x)2= 68727399,34 (функция КВАДРОТКЛ);
-
 (функция
СТЬЮДРАСПОБР).
(функция
СТЬЮДРАСПОБР).

Для построения чертежа используем Мастер диаграмм (точечная) – покажем исходные данные (поле корреляции).

