
- •Задача 1. Обработка результатов наблюдений
- •Построить вариационный (статистический) ряд:
- •Построить для полученного вариационного ряда гистограмму и эмпирическую функцию распределения:
- •Оценить точность выборки.
- •Проверить согласованность теоретического и статистического распределений, используя критерий Пирсона.
- •Задача 2. Статистический анализ связей
- •Список использованной литературы:
Построить для полученного вариационного ряда гистограмму и эмпирическую функцию распределения:
Установим в диалоговом окне программы Гистограмма дополнительно флажки «Интегральный процент» для построения эмпирической функции распределения и «Вывод графика» для построения гистограммы частот. Получим:

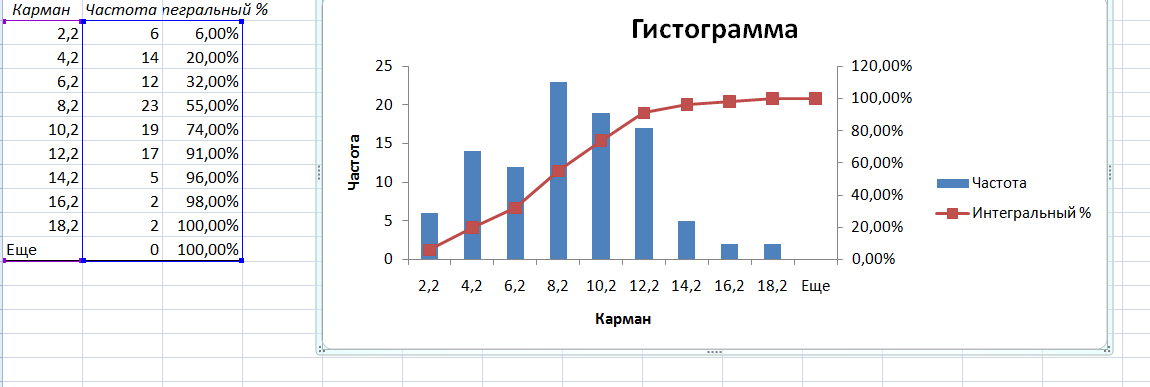
Гистограмма частот наглядно отражает особенности интервального вариационного ряда, в частности позволяет предположить, что величина Х (стаж работы) распределена по нормальному закону.
Эмпирическая функция распределения (интегральный процент) показывает, какова доля сотрудников, стаж работы которых оказался меньше указанной величины («карман»). Так, например, для 5% сотрудников стаж работы менее 2,2 лет; для 80% сотрудников – менее 10,2 лет.
Определить выборочные оценки числовых характеристик случайной величины: выборочную среднюю, медиану, моду, дисперсию, выборочное среднее квадратическое отклонение, коэффициент вариации, коэффициент асимметрии и коэффициент эксцесса.
Для определения числовых характеристик случайной величины Х воспользуемся сервисом Данные / Анализ данных / Описательная статистика (использование программы требует размещения исходных данных в одном столбце). Для получения результатов следует установить флажок «Итоговая статистика».

В результате получим:

Коэффициент
вариации определим по формуле
 = 0,358. Средние величины (среднее, медиана,
мода) характеризуют значение признака,
вокруг которого концентрируются
наблюдения – центральную тенденцию
распределения:
= 0,358. Средние величины (среднее, медиана,
мода) характеризуют значение признака,
вокруг которого концентрируются
наблюдения – центральную тенденцию
распределения:
-
средняя величина стажа работ по организации составила
 = 7,856 лет.;
= 7,856 лет.;
-
медиана, равная 7,8 лет показывает стаж работ сотрудников: для 50% сотрудников стаж работ не больше, чем 7,856 лет, а для 50% – не меньше, чем 7,856 лет;
-
мода равна 3,6
Наиболее важными
показателями вариации (рассеяния)
наблюдений вокруг средней величины
являются дисперсия выборки S2
= 12,86; выборочное среднее квадратическое
(стандартное) отклонение S
= 3,5; коэффициент вариации
= 35,8%. Невысокая величина коэффициента
вариации
 свидетельствует об однородности
значений признака Х
(стаж работы).
свидетельствует об однородности
значений признака Х
(стаж работы).
Коэффициент асимметрии составил –0,1.
Коэффициент эксцесса равен -0,1. Близкое к нулю значение говорит о том, что рассматриваемое распределение по крутости приближается к нормальной кривой.
Оценить точность выборки.
Примем уровень
значимости
 .
С помощью функции ДОВЕРИТ определим
ошибку выборки – размах доверительного
интервала для математического ожидания
генеральной совокупности:
= 0,7.
.
С помощью функции ДОВЕРИТ определим
ошибку выборки – размах доверительного
интервала для математического ожидания
генеральной совокупности:
= 0,7.

Нижняя и верхняя
границы доверительного интервала для
математического ожидания генеральной
совокупности равны соответственно
![]() =7,8-0,7=7,1
и
=7,8-0,7=7,1
и
![]() =7,8+0,7=8,5.
Таким образом, с надежностью 95% средняя
величина стажа работ по организации
заключена в границах от 7,1 до 8,5 лет.
=7,8+0,7=8,5.
Таким образом, с надежностью 95% средняя
величина стажа работ по организации
заключена в границах от 7,1 до 8,5 лет.
Для оценки точности
выборки рассчитаем относительную ошибку
 = 0,7/7,8=8% и сделаем вывод в соответствии
со схемой:
= 0,7/7,8=8% и сделаем вывод в соответствии
со схемой:

На уровне значимости
 точность выборки следует признать
удовлетворительной.
точность выборки следует признать
удовлетворительной.
Провести выравнивание статистического ряда с помощью нормального закона распределения, в качестве параметров использовать выборочные оценки математического ожидания и среднего квадратического отклонения. Показать на одной диаграмме гистограмму эмпирических частот и теоретическую нормальную кривую.
Для проведения вычислений подготовим таблицу. Занесем в нее границы ai и bi интервалов группировки, середины xi этих интервалов, соответствующие частоты ni.
Построим интегральную
функцию нормального распределения с
параметрами
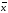 и
и
 .
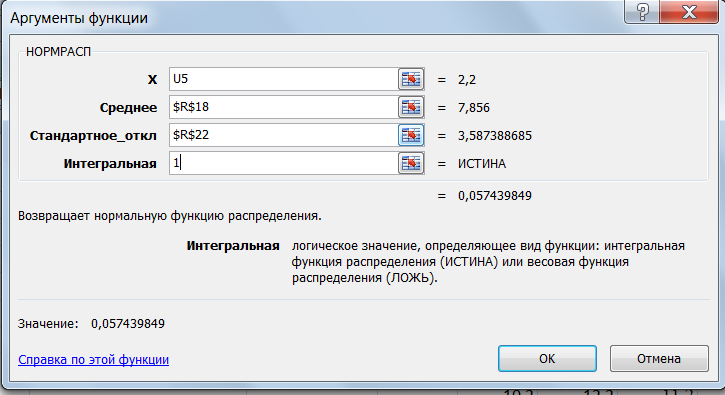
Используем функцию НОРМРАСП; для каждого
интервала в качестве значения, для
которого строится распределение, укажем
верхнюю границу bi.
Для последнего интервала занесем в
таблицу значение
.
Используем функцию НОРМРАСП; для каждого
интервала в качестве значения, для
которого строится распределение, укажем
верхнюю границу bi.
Для последнего интервала занесем в
таблицу значение
 .
.
Определим
теоретические вероятности
 попадания нормально распределенной
величины в i-ый
интервал группировки (для первого
интервала укажем
попадания нормально распределенной
величины в i-ый
интервал группировки (для первого
интервала укажем
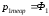 ).
).
Рассчитаем
теоретические частоты
 ,
соответствующие интервалам группировки.
Проверим выполнение условия
,
соответствующие интервалам группировки.
Проверим выполнение условия
 .
.
|
ai |
bi |
xi |
ni |
Ф(х) |
рi теор |
ni теор |
|
0,2 |
2,2 |
1,2 |
6 |
0,05744 |
0,05744 |
5,743985 |
|
2,2 |
4,2 |
3,2 |
14 |
0,154072 |
0,096632 |
9,66318 |
|
4,2 |
6,2 |
5,2 |
12 |
0,322178 |
0,168106 |
16,81063 |
|
6,2 |
8,2 |
7,2 |
23 |
0,538197 |
0,216019 |
21,60187 |
|
8,2 |
10,2 |
9,2 |
19 |
0,743251 |
0,205054 |
20,50542 |
|
10,2 |
12,2 |
11,2 |
17 |
0,887035 |
0,143784 |
14,3784 |
|
12,2 |
14,2 |
13,2 |
5 |
0,961504 |
0,07447 |
7,446962 |
|
14,2 |
16,2 |
15,2 |
2 |
0,989989 |
0,028484 |
2,848433 |
|
16,2 |
18,2 |
17,2 |
2 |
0,998033 |
0,008044 |
0,804443 |
|
суммы |
|
|
100 |
|
|
100 |
Покажем на одной диаграмме гистограмму частот и нормальную кривую:

Диаграмма показывает
соответствие гистограммы частот и
нормальной кривой с параметрами
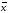 и
и
 .
.
