
Особые точки функций комплексного переменного
Опр.
Особой точкой функции
![]() называется точка в которой
называется точка в которой
![]() не определена или не дифференцируема.
не определена или не дифференцируема.
Опр.
Особая точка называется изолированной,
если
![]() такая ее окрестность, в которой нет
других особых точек.
такая ее окрестность, в которой нет
других особых точек.
Утв. Если
![]() -
изолированная особая точка
-
изолированная особая точка
![]() ,
то в окрестности
,
то в окрестности
![]() ,
,
![]() раскладывается в ряд Лорана.
раскладывается в ряд Лорана.
Классификация особых точек
Опр1. Особая точка называется устранимой, если в ряде Лорана в окрестности этой точки отсутствует главная часть.
Опр2. Изолированная особая точка называется полюсом, если главная часть ряда Лорана в окрестности этой точки имеет конечное число членов:
![]()
Число N называется кратностью (порядком полюса).
Утв.
Если
![]() - полюс
- полюс
![]() ,
то
,
то
![]() .
.
Док-во:
![]()
![]()
![]()
Опр3. Изолированная особая точка называется существенно особой, если главная часть разложения в ряд Лорана в окрестности этой точки содержит бесконечное число членов.
Лекция 8
Связь между нулем и полюсом
Утв1.
![]() имеет в точке
имеет в точке
![]() нуль порядка n
нуль порядка n
![]()
![]() имеет в точке
имеет в точке
![]() полюс порядка n.
полюс порядка n.
Док-во: {![]() }
}
![]()
![]()
![]()
![]()
Утв2.
![]() имеет существенно особую точку в точке
имеет существенно особую точку в точке
![]()
![]()
![]() имеет в
имеет в
![]() неизолированную особую точку ИЛИ
существенно особую точку.
неизолированную особую точку ИЛИ
существенно особую точку.
Пример.
![]() ;
;
![]() ;
;
![]()
![]() ;
;
![]() ;
;
![]()
Таким образом, получаем не изолированную особую точку.
Утв3.
Если
![]() ,
,
![]() ,
,
![]() ,
,
то
![]() имеет при:
имеет при:
1)m![]() n
устранимую особую точку,
n
устранимую особую точку,
2)m>n полюс порядка n-m.
Док-во: {для 2}

![]() ;
;
Теорема Сохоцкого.
Если
![]() -существенно
особая точка функции
-существенно
особая точка функции
![]() ,
то
,
то
![]()
![]() .
.
Док-во:
1)![]()
а)
![]()
![]() -сходится
при
-сходится
при
![]()
![]() сходится при
сходится при
![]()
![]()
б) Предположим противное:
![]()
![]()
![]() ограничена в
окрестности точки
ограничена в
окрестности точки
![]() .
.
в)
![]()
![]()
![]() при
при
![]() (т.е.
(т.е.
![]() ограничена в окрестности
ограничена в окрестности
![]() ).
).
г)В круге
![]()
![]() ограничена, как непрерывная функция в
замкнутой области.
ограничена, как непрерывная функция в
замкнутой области.
д) Из б), в), г)
следует
![]() ограничена на всей комплексной плоскости.
ограничена на всей комплексной плоскости.
 е)
е)
![]() ограничена на С,
ограничена на С,
![]() аналитическая, по теореме Ляувилля
аналитическая, по теореме Ляувилля
![]()
![]() противоречие.
противоречие.
2)
![]()
![]()
а)
![]()
![]()
![]()
![]() имеет
не изолированную особую точку.
имеет
не изолированную особую точку.
б)![]()
![]()
![]() -изолированная
особая точка
-изолированная
особая точка
![]()
![]() имеет изолированную
особую точку в
имеет изолированную
особую точку в
![]()
![]()
![]() имеет существенно особую точку
имеет существенно особую точку
![]() по Утв2
по Утв2
![]() имеет существенно особую точку в
имеет существенно особую точку в
![]()
![]() по
1)
по
1)
![]()
![]()
![]()
Теорема доказана.
Особые точки в бесконечности
Утв.
Если
![]() -изолированная
особая точка
-изолированная
особая точка
![]() ,
то
,
то
![]()
Док-во:
Пусть
![]() .
Раскладываем
.
Раскладываем
![]() в окрестности нуля:
в окрестности нуля:
![]() .
.
Вычеты
Опр.
![]() -изолированная
особая точка.
-изолированная
особая точка.
![]() называется вычетом, где
называется вычетом, где
![]() - коэффициент при -1 степени в разложении
ряда Лорана:
- коэффициент при -1 степени в разложении
ряда Лорана:
![]()
Основная теорема о вычетах.
Если G
– односвязная область, Г – замкнутый
контур, Г ограничевает G,
G
содержит конечное число изолированных
особых точек
![]() функции
функции
![]() ,
то
,
то
![]() .
.
Док-во:
 Г
Г
![]() G
G
![]() .
.
![]() .
.
![]() .
.
![]()
![]()
Окружит каждую
особую точку
![]() окружностью
окружностью
![]() так, чтобы внутри
так, чтобы внутри
![]() не было других особых точек, и чтобы
не было других особых точек, и чтобы
![]() и
и
![]() не пересекались(i
не пересекались(i![]() j).
j).
![]() .
.
Вычисление вычетов
1.
Утв.
Если
![]() - устранимая особая точка
- устранимая особая точка
![]() ,
то
,
то
![]() (Т.к.
главная часть ряда Лорана не содержит
ни одного члена
(Т.к.
главная часть ряда Лорана не содержит
ни одного члена
![]() )
)
2.
а) Утв.
Если
![]() -простой
полюс
-простой
полюс
![]() (полюс
кратности 1), то
(полюс
кратности 1), то
![]() .
.
Док-во:
![]()
![]()
Пример.
![]() ,
,
![]()
![]() имеет простой полюс.
имеет простой полюс.
![]()
б) Утв.
Если
![]() ,
,![]() ,
,![]() ,
,![]() ,
то
,
то
![]() .
.
Док-во:
![]() -полюс
I
порядка
-полюс
I
порядка
![]()
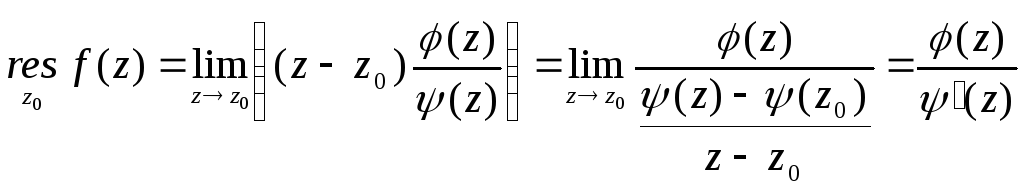
3.
Утв.
Если
![]() -полюс
порядка n
-полюс
порядка n
![]() ,
то
,
то
![]() .
.
Док-во:
![]()
![]()
![]()
![]()
Переходим к
![]() и делим на
и делим на
![]() :
:
![]()
Пример1.
![]() ;
;
Пример2.
![]()
Лекция 9
Опр.
![]() - изолированная особая точка
- изолированная особая точка
![]() ,
,
![]() ,
где Г- замкнутый контур.
,
где Г- замкнутый контур.
Утв.
Если
![]() ,
то
,
то
![]() .
.
Док-во:
1)
![]() .
.
2) С: {![]() }
}
![]() ,
,
![]()
при
![]()
![]()
3)![]()
![]()
4)
![]()
![]()
Теорема.
Если
![]() -изолированная
особая точка, кроме
-изолированная
особая точка, кроме
![]() имеется конечное число особых точек,
то
имеется конечное число особых точек,
то
![]()
Док-во:
Возьмем замкнутый
контур С, охватывающий все особые точки,
кроме
![]()
![]() ;
;
![]() ;
;
![]()
![]() ;
;
Логарифмический вычет.
Опр. Логарифмическим вычетом называется:
![]() ,
если С – замкнутый контур,
,
если С – замкнутый контур,
![]() - аналитическая внутри С и на нем за
исключением конечного числа особых
точек, все особые точки лежат внутри С,
все особые точки – полюсы.
- аналитическая внутри С и на нем за
исключением конечного числа особых
точек, все особые точки лежат внутри С,
все особые точки – полюсы.
Утв1.
Если
![]() ,
,
![]() -
нуль кратности
-
нуль кратности
![]() фунции
фунции
![]() ,
то
,
то
![]() .
.
Док-во:
![]()
![]()

Для функции
![]()
![]() -
полюс I
порядка.
-
полюс I
порядка.
![]() .
.
Утв2.
Если
![]() -полюс
кратности n
функции
-полюс
кратности n
функции
![]() ,
то
,
то
![]() .
.
Док-во:

![]() .
.
Принцип аргумента.
Теорема.
Логарифмический вычет функции
![]() относительно контура С равен приращению
относительно контура С равен приращению
![]() аргумента
аргумента
![]() при обходе контура С, деленному на
при обходе контура С, деленному на
![]() ,
равно разности между числом нулей М и
числом полюсов N
функции
,
равно разности между числом нулей М и
числом полюсов N
функции
![]() в облости D,
ограниченной контуром С:
в облости D,
ограниченной контуром С:
![]()
Д ок-во:
ок-во:
Z W

z w
C
1)
![]()
2) Внутри С
![]() будет иметь конечное число нулей, т.к.
она аналитическая в замкнутой области.
В силу Утв1 и Утв2 :
будет иметь конечное число нулей, т.к.
она аналитическая в замкнутой области.
В силу Утв1 и Утв2 :
![]()
3)
![]()
Теорема Руше.
ЕСЛИ G
– односвязная область, С – замкнутый
контур, ограничивающий G,
![]() и
и
![]() аналитические в G
и на С,
аналитические в G
и на С,
![]() на
С,
на
С,
![]() на
С,
на
С,
![]() -
сумма кратностей всех лежащих в G
нулей функции
-
сумма кратностей всех лежащих в G
нулей функции
![]() ,
,
![]() -
сумма кратностей всех лежащих в G
нулей функции
-
сумма кратностей всех лежащих в G
нулей функции
![]() +
+![]() ,
ТО
,
ТО
![]() .
.
Док-во:
1)
![]()
2 )
)
![]()
3)
![]()
![]()
w
Вектор из начала
координат в точку, при такой конфигурации
образа С, ни одного оборота не совершит.
![]() .
.
4)
![]()
Пример.
Найти количество нулей, которые имеет
функция
![]() в круге
в круге
![]() .
.
![]() ,
,
![]()
при
![]() :
:
![]()
![]()
![]() имеет нуль кратности
5
имеет нуль кратности
5
![]() w
имеет 5 нулей.
w
имеет 5 нулей.
Утв.
Если
![]() ,
то
,
то
![]() имеет n
корней.
имеет n
корней.
Док-во:
![]()
![]()
С:
![]()
![]() имеет
нуль кратности n,
т.о.
имеет
нуль кратности n,
т.о.
![]() имеет n
нулей.
имеет n
нулей.
Теорема.
Если
![]() ,
,
![]() аналитическая в G
аналитическая в G
![]() ,
то
,
то
![]() - аналитическая.
- аналитическая.
Док-во:
![]()
![]()
1)
![]()
![]()
![]()
![]()
-
аналогично доказываем

-
Из пунктов 1) и 2) следует, что для F выполнены условия Коши-Римана, следовательно F аналитическая.
Лекция 10
Вычисление несобственных интегралов с помощью вычетов
Теорема.
Если
![]()
![]() при x=z,
при x=z,
![]() -изолированная
особая точка f(z),
-изолированная
особая точка f(z),
![]() имеет в
имеет в
![]() нуль не ниже II
порядка,
нуль не ниже II
порядка,
![]() не имеет особых точек на действительной
оси,
не имеет особых точек на действительной
оси,
![]() имеет конечное число особых точек, то
имеет конечное число особых точек, то
![]() ,
где
,
где
![]() распространяется
на особые точки, лежащие выше действительной
оси.
распространяется
на особые точки, лежащие выше действительной
оси.
Док-во:
Возьмем круг такого радиуса, чтобы на нем и вне его не было особых точек, кроме бесконечности.

Y
R
-R R x

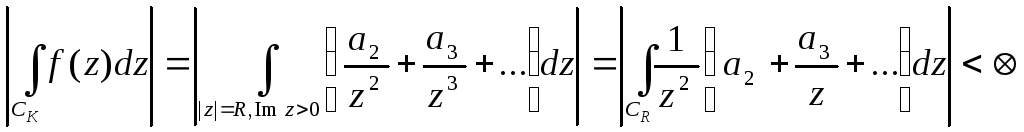
![]()
![]() .
.
Пример.
Найти интеграл:![]() .
.
![]() ,
,
![]() ;
;
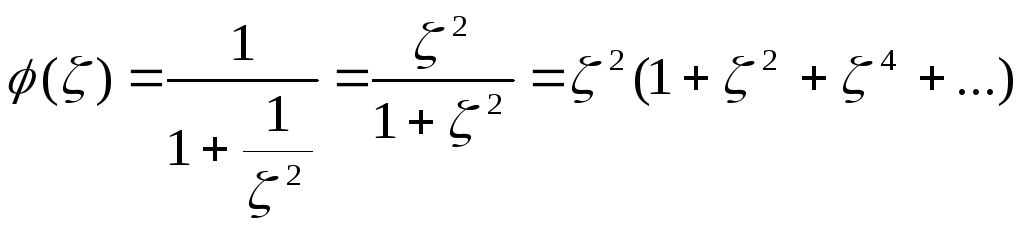
![]()
Операционное исчисление
Опр.
Функция
![]() называется оригиналом, если:
называется оригиналом, если:
1)
![]() определена при
определена при
![]() ,
,
![]() и
и
![]() являются
кусочно-непрерывными на любом конечном
интервале,
являются
кусочно-непрерывными на любом конечном
интервале,
2) при
![]()
3)![]() .
.
Утв.
Если
![]() -многочлен
степени n,
-многочлен
степени n,
![]() то
то
![]() .
.
Док-во:
![]() ,
,
![]() по
правилу Лопиталя
по
правилу Лопиталя
![]()
![]() ;
;![]() .
.
Опр.
![]() называется изображением, соответствующим
оригиналу f(t),
если F(p)
– интеграл Лапласа:
называется изображением, соответствующим
оригиналу f(t),
если F(p)
– интеграл Лапласа:
![]() ;
;
![]() .
.
Теорема.
Если f(t)
оригинал, то
![]() -
изображение
-
изображение
![]() ,
,
1)
![]() сходится
в полуплоскости
сходится
в полуплоскости
![]() ,
,
2)
![]() является
в полуплоскости
является
в полуплоскости
![]() аналитической функцией от p.
аналитической функцией от p.
Док-во:
1)![]()
![]()
![]()
![]() ,
таким образом F(p)
сходится.
,
таким образом F(p)
сходится.
2) Аналитичность следует из теоремы, доказанной в предыдущей лекции.
След. Если F(p)
– изображение некоторого оригинала,
то
![]()
Зам. Если
![]() ,
то F(p)
сходится равномерно.
,
то F(p)
сходится равномерно.
Свойства преобразования Лапласа:
-
Линейность
![]()
-
Однородность.
![]() .
.
Док-во для 2:
![]()
Теорема о дифференцировании оригинала.
Если f(t)
– оригинал,
![]() -оригинал,
F(p)-изображение
f(t),
-оригинал,
F(p)-изображение
f(t),
![]() ,
,
то
![]() .
.
Док-во:
![]()
![]()
![]()
![]() .
.
Следствие.
Если
![]() -оригиналы,
то
-оригиналы,
то
![]() .
.
Док-во:
![]()
![]()
далее по индукции.
Теорема о дифференцировании изображения.
Если
![]() ,
то
,
то
![]() .
.
![]()
Теорема об интегрировании оригинала.
Если
![]() ,
то
,
то
![]() .
.
Док-во:
1) Докажем, что
![]() -оригинал.
а)
кусочная гладкость – по свойству
интеграла.
-оригинал.
а)
кусочная гладкость – по свойству
интеграла.
б)
![]() ,
t>0
–очевидно.
,
t>0
–очевидно.
в)
![]()
2)
![]() .
.
![]() .
.
Лекция 11
Теорема об интегрировании изображения
Если f(t)
– оригинал,
![]() –
оригинал, то
–
оригинал, то
![]() .
.
Док-во:
![]()
![]() .
.
![]() ,
,
![]()
![]()
![]()
![]()
![]()
![]() .
.
Теорема о запаздывание
Если
![]() -оригинал,
-оригинал,
![]() ,
,
![]() то
то
![]() .
.
Док-во:
![]() .
.
Теорема смещения
Если
![]() ,
то
,
то
![]() .
.
Таблица соответствий
1.
![]() .
.
![]()
![]()
2.
![]()
![]()
3.
![]()
![]()
4.
![]()
5.
![]()
6.
![]()
![]()
![]() .
.
7.
![]()
![]() .
.
8.
![]()
9.
![]()
10.
![]()
11.
![]()
12.
![]()
13.
![]()
14.
![]()
![]()
15.
![]()
![]()
Опр. Сверткой функций f и g называется
![]()
Утв.
Если
![]() ,
g(t)
– оригиналы, то f*g(t)
– оригинал.
,
g(t)
– оригиналы, то f*g(t)
– оригинал.
Док-во:
Пункты 1) и 2) в определении оригинала очевидно выполнены. Докажем выполнение пункта 3).
![]() ,
,
![]() ,
где
,
где
![]()
![]()
Теорема о свертках.
Если f(t),
g(t)
– оригиналы,
![]() ,
,
![]() ,
то
,
то
![]() .
.
Док-во:
![]()
![]() .
.
Лемма Жордана
Лемма1.
Если f(z)
– аналитическая в верхней полуплоскости,
за исключением, быть может, конечного
числа точек,
![]()
![]()
![]() -
полуокружность в верхней полуплоскости
-
полуокружность в верхней полуплоскости
![]() .
.
Док-во:
![]()
![]()
![]()
![]()

 ;
;
![]()
![]()
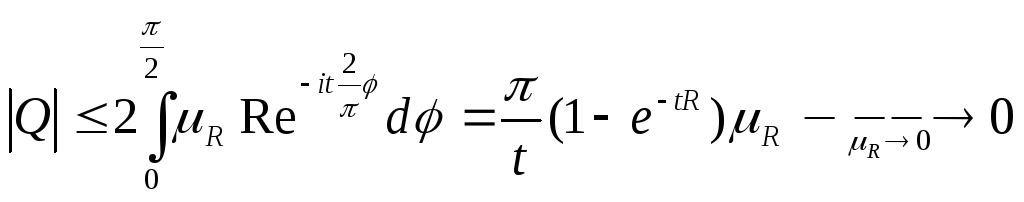 .
.
Лекция12
Лемма2.
Если f(z)
– аналитическая в левой полуплоскости,
![]() ,
,
![]() то
то
![]() .
.
Док-во:
![]()
![]()
![]() .
.
Лемма3.
Если f(z)
аналитическая,
![]() ,
,
![]() то
то![]() .
.
 y
y
![]()
R
![]() x
x
![]()
Док-во:
-
Докажем, что
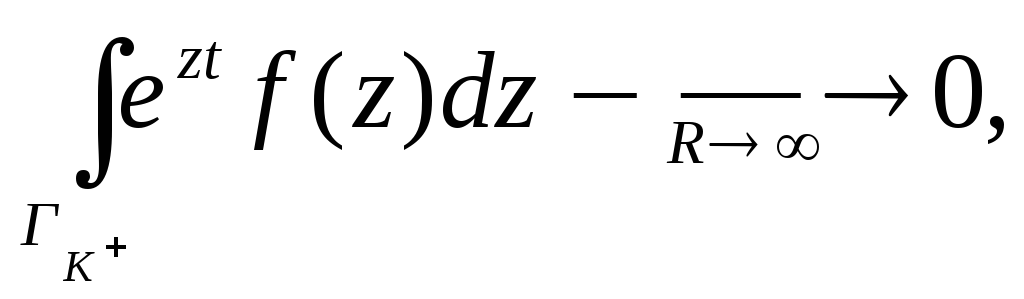
 .
.
![]()
![]() .
.

2)Если
![]() аналогично.
аналогично.
3)
![]() по Лемме 2.
по Лемме 2.
4) Из пунктов
1), 2), 3) следует
![]() .
.
Лемма4.
Если f(z)
аналитическая
 ,
,
![]() ,
,
![]() то
то
![]()
Докозательство следует из Леммы3.
Теорема об интеграле Фурье.
Если f(t)
кусочно непрерывна и кусочно дифференцируема
на R,
то
![]() (сходится
абсолютно).
(сходится
абсолютно).
Теорема обращения преобразования Лапласа.
Если f(t)
– оригинал,
![]() ,
то
,
то
![]() .
.
![]()
Док-во:
![]() ;
;
![]()
![]() ;
;
![]() ;
;
Теорема разложения.
![]() ,
для
,
для
![]() выполнены условия леммы Жордана, то
выполнены условия леммы Жордана, то
 .
.
Док-во:
 .
.
Пример.
![]() ;
;
![]() ;
;
![]()
![]() .
.
Лекция13
