Элементарные функции комплексного переменного.
Значение целой положительной степени комплексного аргумента, значение функции f(z) = z n , проще всего вычислять в тригнометрической форме. Если z = x + iy = r (cos + isin ), то для любого целого положительного числа n имеет место формула: w = f(z) = z n = r n (cos n + isin n ). Если w = f (z) = f (x + iy) = u(x, y) + iv(x, y), то u(x, y) = r ncos n , u(x, y) = r nsin n.
Корнем
n-й степени из
комплексного числа z
называется число
такое,
что wn
= z.
Для любого
комплексного числа z
существует n
комплексных чисел w
таких, что wn
= z.
Значение корня,
т.е. значение функции
проще
всего вычислять в тригнометрической
форме.
Если z
= x
+ iy
= r
(cosj
+ isinj),
то для любого целого положительного
числа n имеет
место формула:
Т.е.
функция
является
многозначной функцией _
каждому значению аргумента отвечает
n различных значений
корня.
Если
w
= f(z)
= f(x
+ iy)
= u(x,
y) + iv(x,
y), то
Если z = x + iy = r (cos + isin ), то значения функции f(z) = exp(z) вычисляются по формуле f(z) = ez = ex+iy = e xe y = ex (cosy + isiny). Если w = f(z) = f(x + iy) = u(x, y) + iv(x, y), то u(x,y) = ex cosy , v(x,y) = ex siny.
Тригонометрические
функции комплексного
аргумента определяются формулами:
Гиперболические
функции комплексного
переменного определяются совершенно
так же, как функции в действительной
области:
Логарифмом комплексного числа z называется такое число w, что exp(w) = z. Значения логарифмической функции f(z) = Ln(z) вычисляются по формуле Ln(z) = ln(|z|) + iArg z = ln(|z|) + iarg z + 2kp i, k = 0, .1, .2,... Величину ln(|z|) + iarg z называют главным значением логарифма. Функция (z) = Ln(z) является многозначной функцией _ каждому значению аргумента отвечает бесконечное множество различных значений логарифма.
ПРИМЕР 6. Вычисление значений логарифма комплексного числа.
Показательная (f(z) = az) и степенная (f(z) = za) функции комплексного переменного определяются с помощью логарифма - для любых комплексных чисел a и z справедливо: f(z) = az = ezLna; f(z) = za= eaLnz.
Значения
обратных тригонометрических
функций комплексного
переменного вычисляются по формулам:
.
Дифференцирование функций комплексного переменного.
Производная
функции комплексного переменного
определяется, как и производная в
действительной области:
Здесь
z0,
z
_
комплексные и f(z0)
= f(z0+z)
- f(z).
Используя это определение и свойства пределов, несложно убедиться в справедливости следующих правил дифференцирования.
1.
Сумма и произведение дифференцируемых
в точке функций, есть функция и
справедливы равенства:
2.
Частное дифференцируемых в точке
функций, при условии, что знаменатель
в точке не равен нулю, есть дифференцируемая
в этой точке функция, :
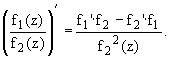
3.
Сложная функция
f(
(z))
дифференцируема в точке z0,
если в этой точке дифференцируема
функция
(z),
а функция f(u)
дифференцируема в точке u0,
где
u0
=
(z0)
и u
=
(z).
При этом в точке z0
имеет место формула:
Для элементарных функций комплексного переменного справедливы формулы дифференцирования, установленные для действительных значений аргумента. Например, рассмотрим функцию f(z) = z3. По определению производной для любой точки z, принадлежащей комплексной области, записываем:
Предел существует для любой точки z, принадлежащей комплексной области и (z3)' =3z2. Аналогично можно получить: (zn)' = nzn-1 (n - действительное число).
Если f(z) = f(x+iy) = u(x, y) + iv(x, y), т.е. u(x, y) = Re f(z) и v(x, y) = Im f(z), то справедливы следующие утверждения:
1. Если функция f(z) дифференцируема в точке, то в этой точке существуют частные производные ее действительной и мнимой частей u(x, y) = Re f(z), v(x, y) = Im f(z) и выполняется условие Коши-Римана:
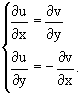
2. Если u(x, y) и v(x, y) дифференцируемы в точке (x0, y0) (имеют непрерывные частные производные в этой точке) и выполняется условие Коши-Римана, то функция f(z) = f(x+iy) = u(x, y) + iv(x, y) дифференцируема в точке z0 = x0+ iy0.
3. Производная дифференцируемой функции может быть записана по одной из формул:
