П1
.6.docПрактическое занятие 1.6
расчет балок на прочность при изгибе.
В проектировочных расчетах конструкций необходимо учитывать соблюдение условия прочности, заключающееся в том, что максимальные нормальные напряжения, возникающее в точках сечения, не должны превышать допускаемых для данного материала:
где
- максимальный изгибающий момент;
- момент сопротивления поперечного
сечения;
- допускаемое нормальное напряжение.
Рассмотрим двухопорную балку, показанную
на рисунке 1. Для заданной балки необходимо
построить эпюры поперечных сил и
изгибающих моментов. Из условия прочности
по нормальным напряжениям подобрать
сечение двутавра, окружности и
прямоугольника с соотношением сторон
и сравнить их площади. В расчетах принять
,
;
;
.
Расстояния на рисунке 1 заданы в метрах
1. Определяем опорные реакции из условия равновесия
Проверка
Проверка выполняется, опорные реакции определены верно.
2. Запишем выражения для поперечных сил и изгибающих моментов.
I участок:
При
:
При
:
рис. 1
II участок:
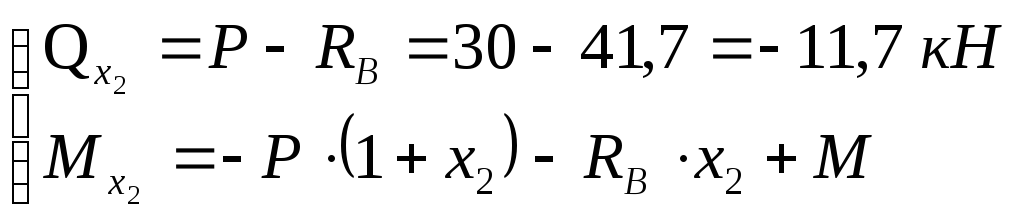
При
:
.
При
:
III участок:
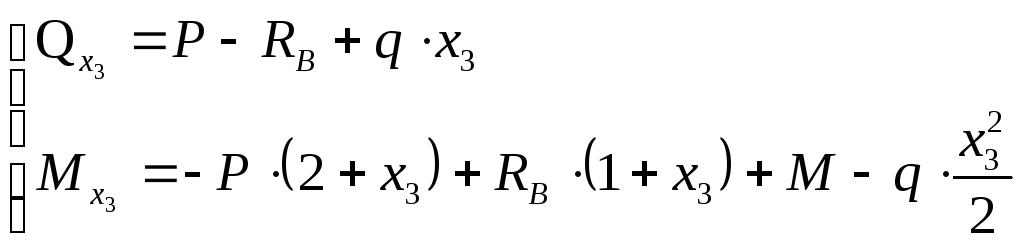
При
:
;
.
При
:
;
Поперечная сила меняет знак, значит, на эпюре изгибающих моментов будет экстремум в сечении, где поперечная сила равна нулю
IV участок:
При
:
;
.
При
:
;
3. Находим момент сопротивления балки из условия прочности по нормальным напряжениям.
,
где
- максимальный изгибающий момент, взятый
из эпюры изгибающих моментов.
4. подбираем поперечные сечения балки.
4.1 Балка двутаврового сечения
Подбираем двутавр № 22, у которого
и площадь поперечного сечения
.
4.2 Прямоугольное сечение
,
тогда
Площадь сечения
4.3 Круглое сечение балки.
Площадь сечения
5. Сравниваем полученные площади
;
и
Делает вывод, что наиболее экономичным является двутавровое сечение.