П1

Практическое занятие 1.3

плоское напряженное состояние

При практических расчетах наиболее часто удается определить нормальные и касательные напряжения на некоторых двух взаимно перпендикулярных площадках. Пусть, например, по граням элемента действуют показанные напряжения (рис. 1). Необходимо найти главные напряжения и соответствующие им главные напряжения (Обратная задача в теории плоского напряженного состояния).

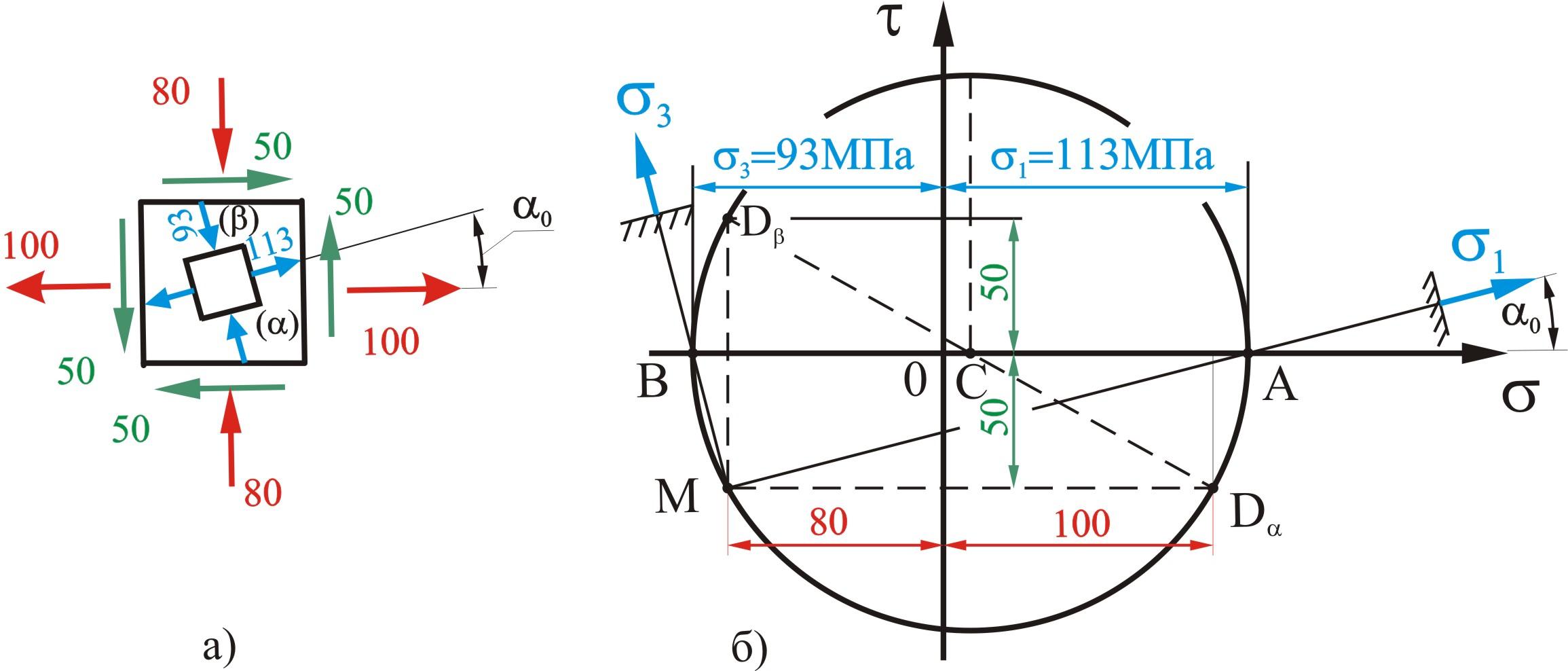
Рис. 1

Если обозначить площадки так, как показано на рис. 1, а, то

МПа; МПа;

МПа; МПа.

Определим главные напряжения

МПа

МПа.

Так как значение одного из напряжений получилось отрицательным, его обозначим как .

Тангенс угла наклона главного напряжения к оси

Выполним графическое решение данной задачи.

В геометрической плоскости в системе координат нанесем точку с координатами , (рис. 3.1, б) и точку с координатами , . Соединим точки и . Полученный отрезок пересекает ось в точке . Радиусом проводим окружность с центром в точке . Абсциссы точек пересечения полученной окружности с осью дадут соответственно величины главных напряжений и .

Для определения положения главных площадок найдем полюс и воспользуемся его свойством. Для этого из точки проведем линию действия напряжения , т. е. горизонталь. Точка пересечения этой линии с окружностью и является полюсом. Соединяя полюс с точками и , получим направления главных напряжений и соответственно. Главные площадки перпендикулярны к найденным направлениям главных напряжений.

После определения положения главных площадок и значений главных напряжений и можно определить нормальные и касательные напряжения для любой произвольной площадке, расположенной под углом к главным. Например, на главных площадках, расположенных как указано на рис. 3.2, а, действуют главные напряжения и . Требуется найти нормальные и касательные напряжения по граням элемента, одна из которых наклонена к горизонтали под углом .

Произвольным образом обозначаем площадки () и () и проводим нормаль . Из предыдущего расчета МПа; МПа. С учетом расположения главных площадок к горизонтали (), Угол между направлением главного напряжения и нормалью к площадке () будет равен . Угол отрицателен, так как здесь он отсчитывается по часовой стрелке.

Решим сначала эту задачу аналитически.

МПа

МПа

МПа

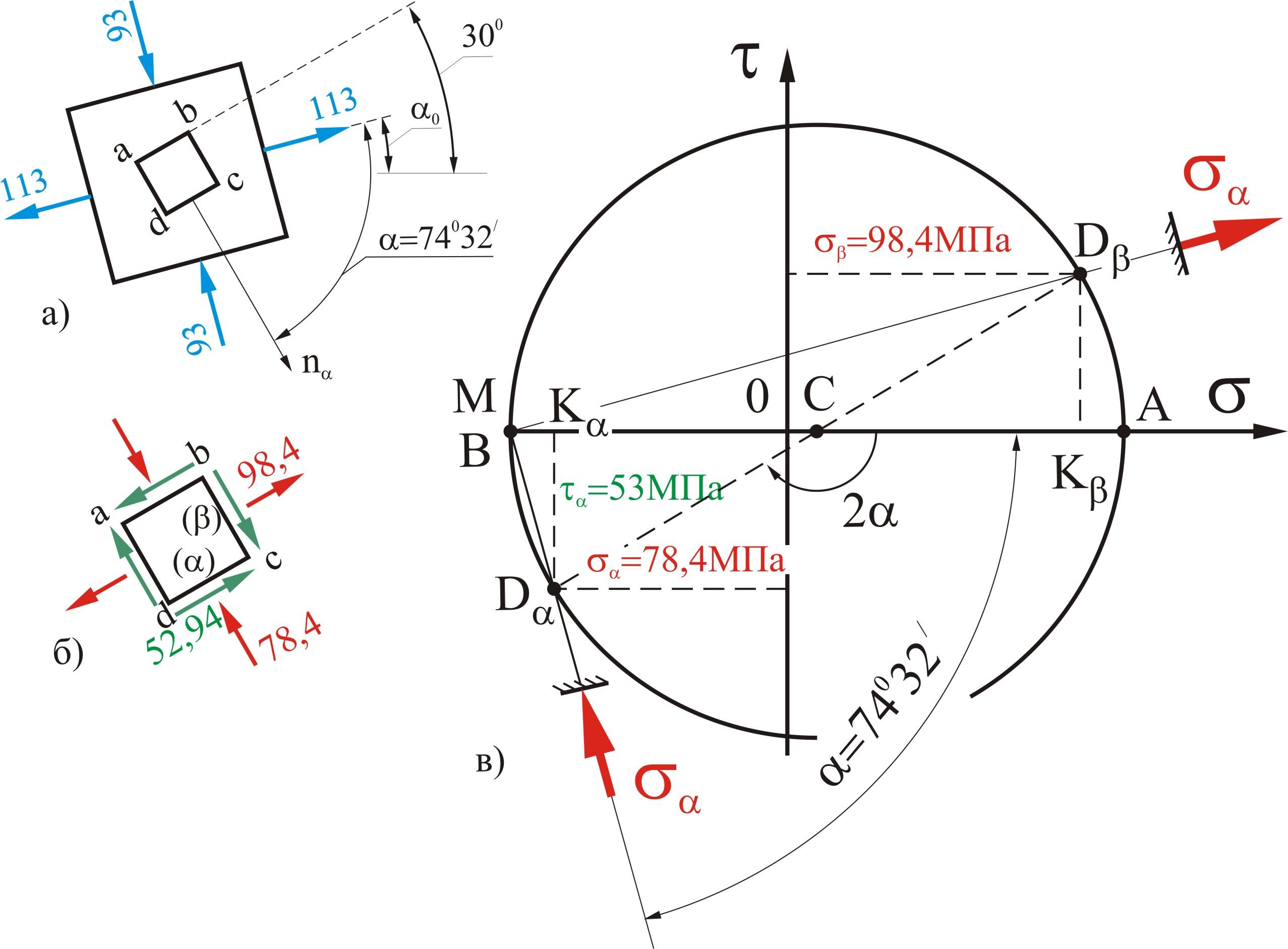
Рис. 2

Учитывая знаки вычисленных напряжений, покажем напряжения на гранях элемента (рис. 2, б).

Для графического решения в геометрической плоскости в системе координат нанесем точки и с координатами и соответственно (рис.2, в)

На отрезке как на диаметре строим круг Мора с центром в точке . Для определения напряжения на площадке () из центра проводим луч под углом до пересечения с окружностью в точке (так как угол имеет отрицательное значение, откладываем его против часовой стрелки).

Координаты полученной точки дадут нам напряжения на площадке ()

МПа; МПа.

Координаты точки дадут нам напряжения на площадке ()

МПа; МПа.

Получаем те же значения напряжений, которые были вычислены ранее.

3