П1

Практическое занятие 1.2

Геометрические характеристики плоских сечений.

При определении положения главных осей и величин главных центральных моментов инерции сложного профиля, состоящего из простых частей можно руководствоваться следующим порядком:

1. провести произвольную систему прямоугольных координат. Разбить фигуру на простые части и определить положение ее центра тяжести;

2. провести начальную систему центральных осей , так, чтобы вычислить моменты инерции частей фигуры относительно этих осей было наиболее просто; определить моменты инерции , , сложного сечения;

3. определить угол наклона главных центральных осей;

4. определить значения главных центральных моментов инерции сложного сечения.

Рассмотрим плоское сечение, показанное на рис.1.

1. Для заданного составного сечения выберем произвольно систему координат -.

Лучше всего проводить координатные оси так, что бы они совпадали с главными осями инерции составных площадей. Поскольку сложное сечение условно можно разложить на полукруглое сечение с радиусом ,мм и двутавровый профиль №22, ось направим так, что бы она совпадала с главной осью инерции полукруга, а ось так, что бы она совпадала с главной осью инерции двутаврового профиля.

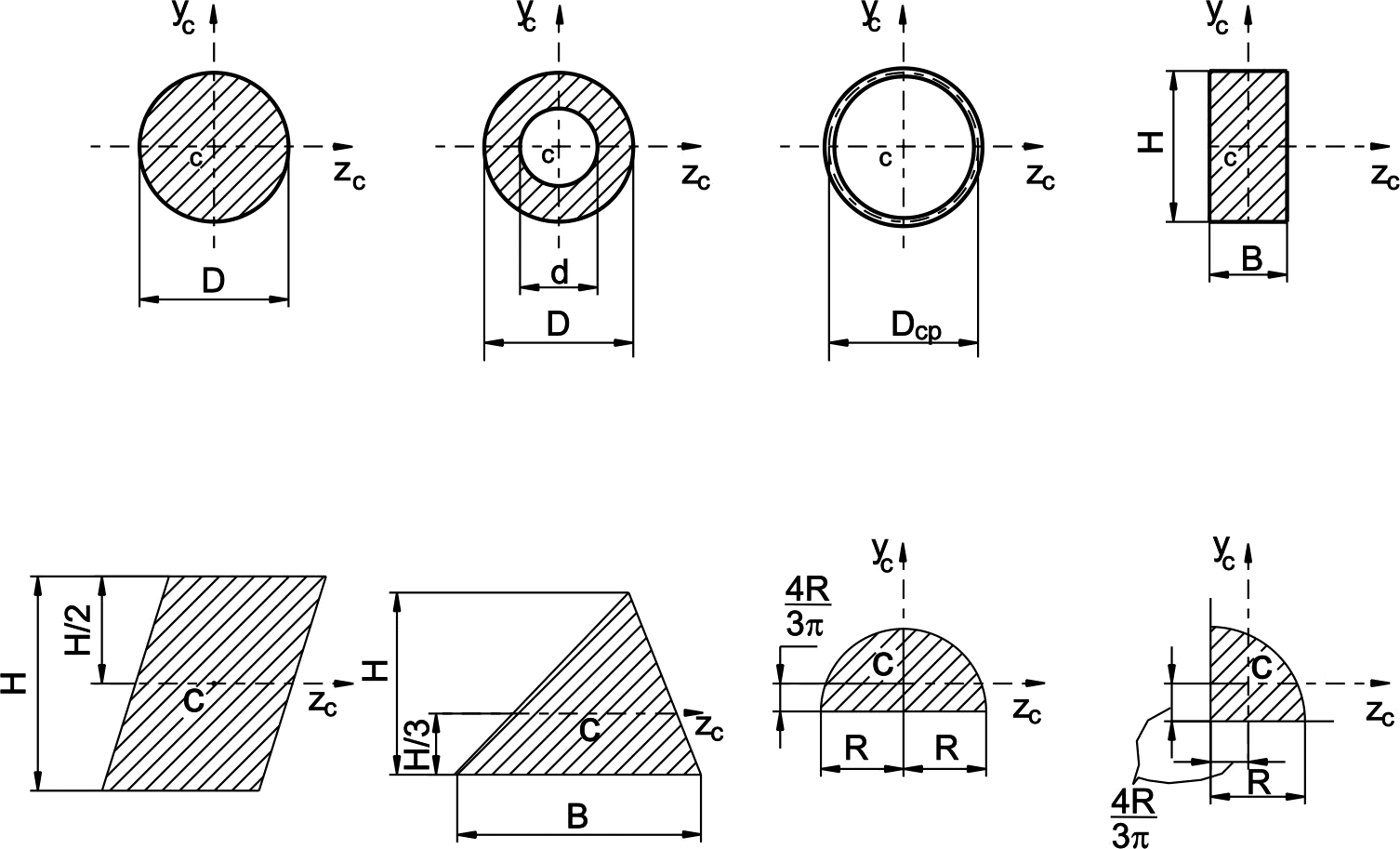
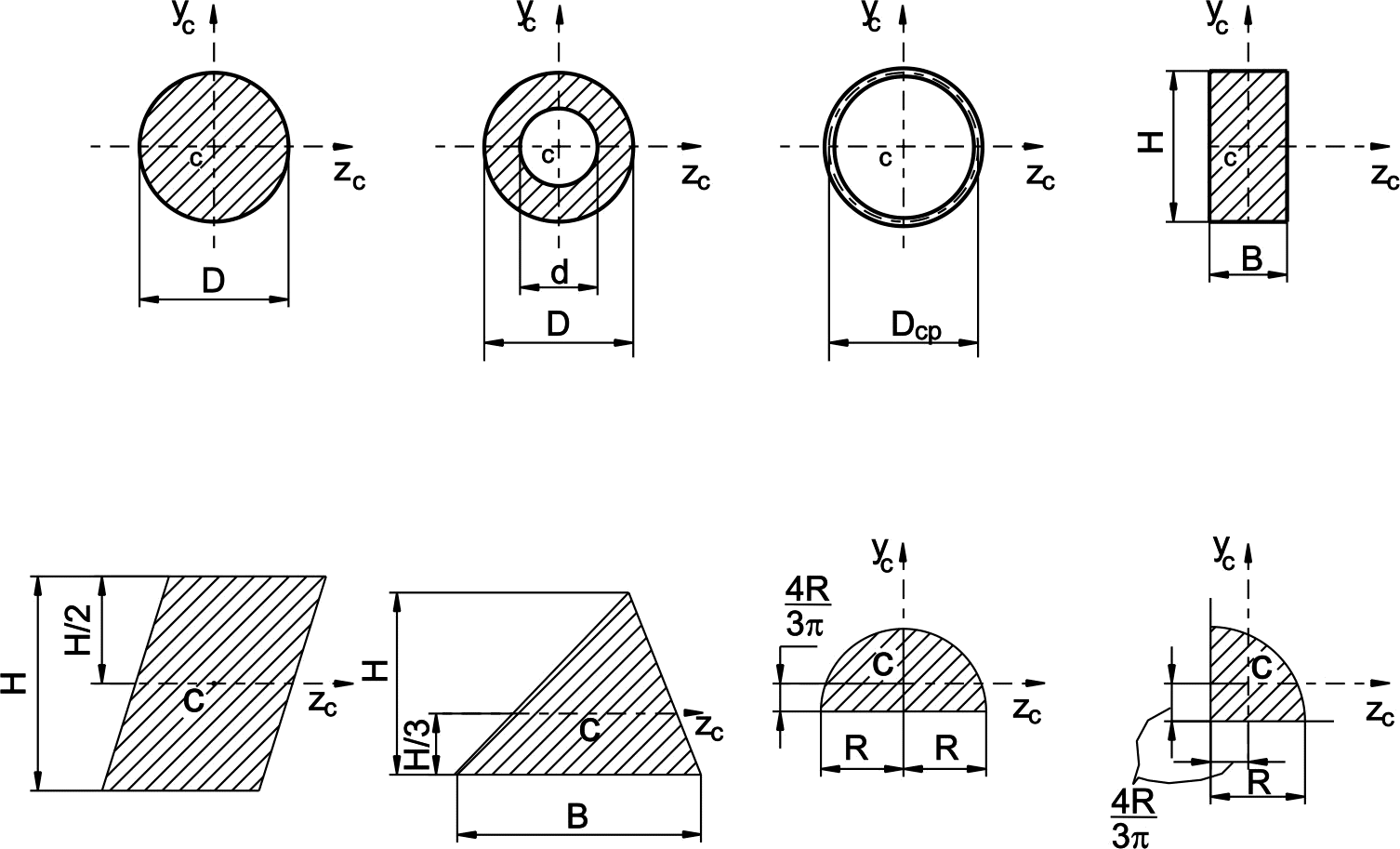
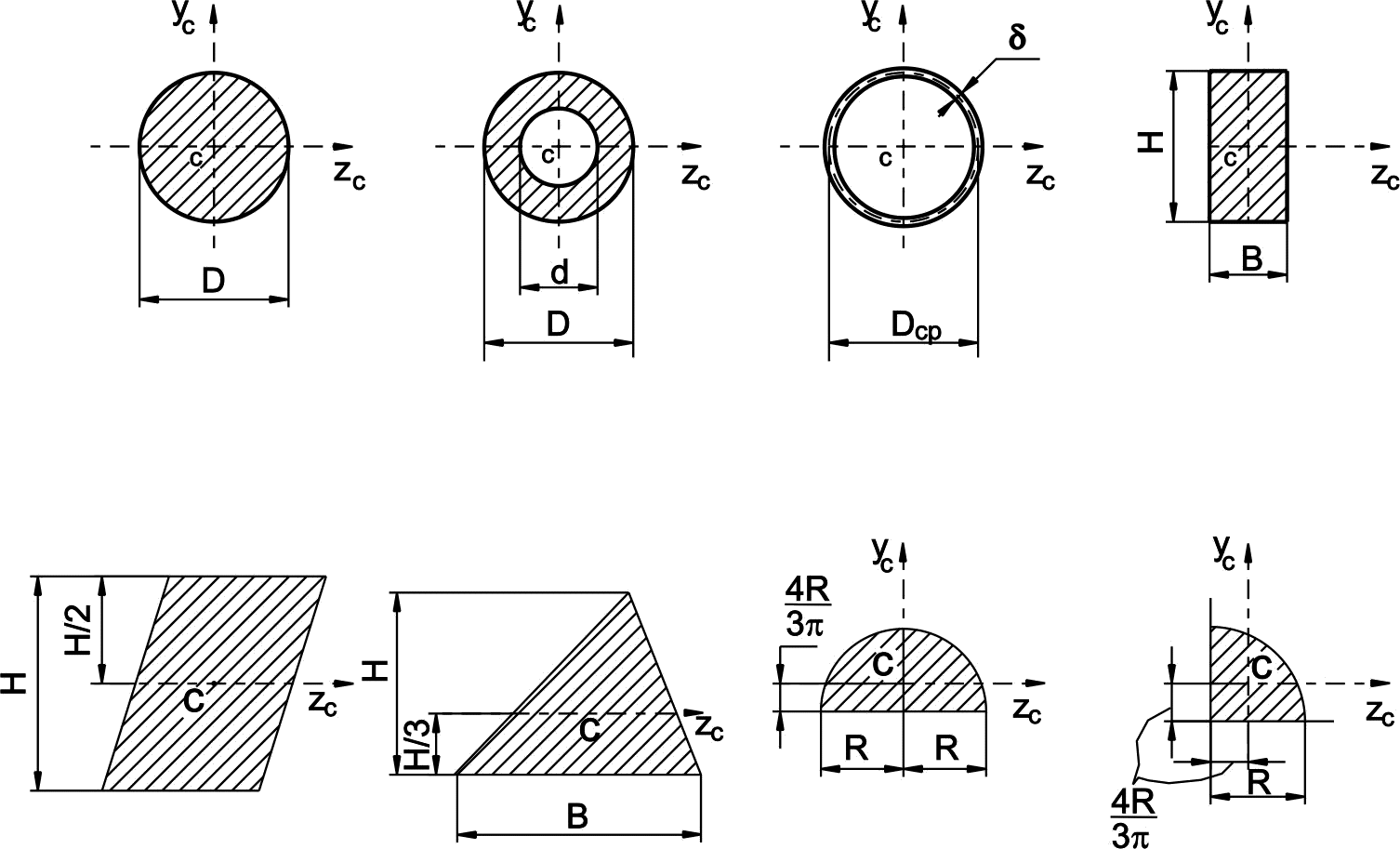
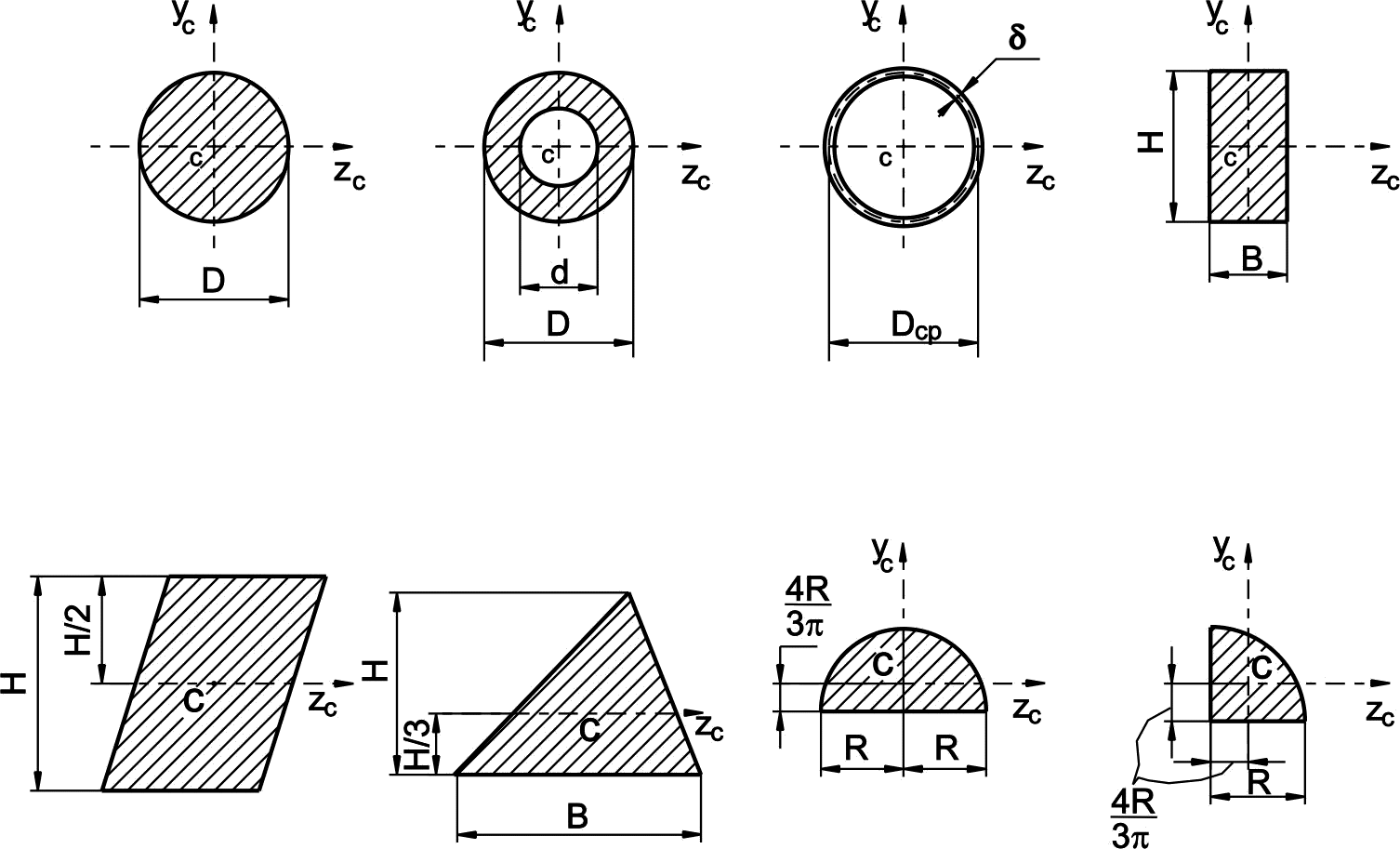
Положение центра тяжести полукруглого сечения по таблице 1:

мм.

Положение центра тяжести двутаврового сечения определяется по сортаменту (Приложение 1 [¹])

Координаты центра тяжести полукруглого сечения в системе координат - можно определить по рис 1

мм; мм

Координаты центра тяжести двутаврового сечения в системе координат -_:

мм , мм

Площадь полукруглого сечения:

, мм²

Площадь двутаврового сечения берется из сортамента (Приложение 1 [Error: Reference source not found]):

мм²

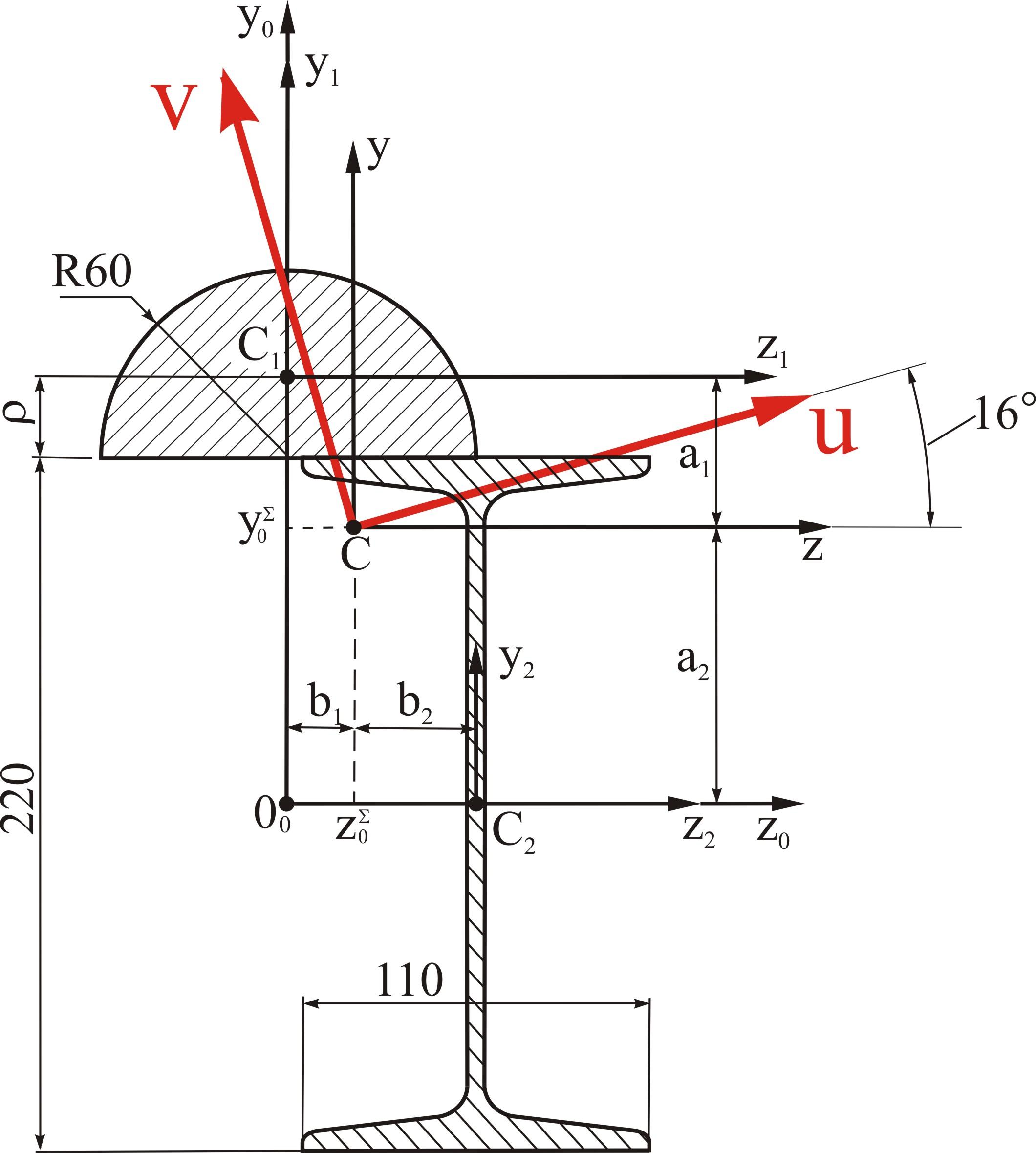
Рис. 2.1

Координаты центра тяжести суммарного сечения в системе координат -, состоящего из полукруглого и двутаврового сечения:

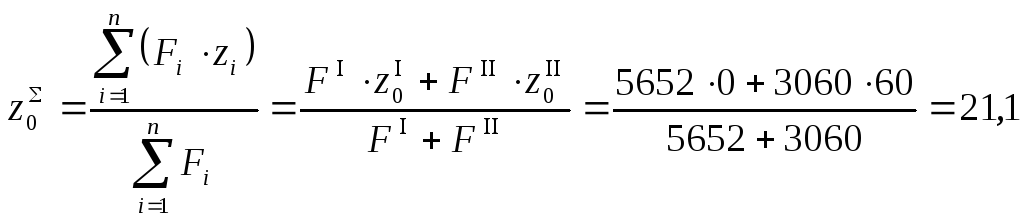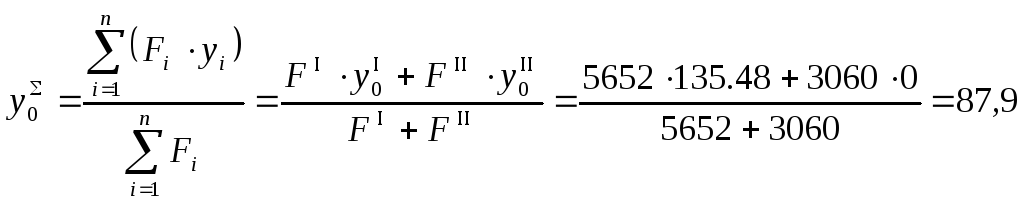мм

мм

2. Проведем начальную систему центральных осей -, параллельных главным центральным осям полукруглого и двутаврового сечений. Моменты инерции , , сложного сечения будем вычислять как сумму моментов инерции полукруглого и двутаврового сечений. Для этого сначала запишем значение моментов инерций данных сечений относительно их главных центральных осей, а потом определим моменты инерций этих сечений относительно начальной системе центральных осей -.

Осевой момент инерции полукруглого сечения, относительно главных центральных осей полукруглого сечения -:

, мм⁴

, мм⁴

Осевой момент инерции двутаврового сечения относительно его главных центральных осей -_:

мм⁴

мм⁴

Центробежные моменты инерции полукруглого и двутаврового сечений относительно их главных осей инерций равны нулю:

, мм⁴

, мм⁴

Для определения осевых моментов инерции полукруглого и двутаврового сечений относительно начальных центральных осей, параллельных главным осям инерции каждого из сечений, найдем расстояния между соответствующими осями.

мм

, мм

, мм

, мм

Осевые моменты инерций полукруглого и двутаврового сечений, относительно начальных центральных осей суммарного сечения , :

, мм⁴

, мм⁴

мм⁴

мм⁴

Осевые моменты инерций суммарного сечения, относительно начальных центральных осей суммарного сечения ,

, мм⁴

,мм⁴

Центробежные моменты инерции полукруглого и двутаврового сечений относительно центральных осей суммарного сечения ,

, мм⁴

,мм⁴

Отметим, что координаты и следует подставлять с учетом их знаков. Центр тяжести полукруглого сечения лежит в области отрицательных значений в системе координат -, поэтому значение величины подставлено со знаком минус. Положение центра тяжести двутавра лежит в отрицательной области значений в системе координат -, поэтому значение величины подставлено со знаком минус.

Центробежный момент инерции суммарного сечения относительно начальных центральных осей ,

, мм⁴

3. Угол наклона главной центральной оси суммарной площади к начальной центральной оси определится из зависимости

Проведем главные центральные оси составного сечения

4. Главные центральные моменты инерции суммарного сечения

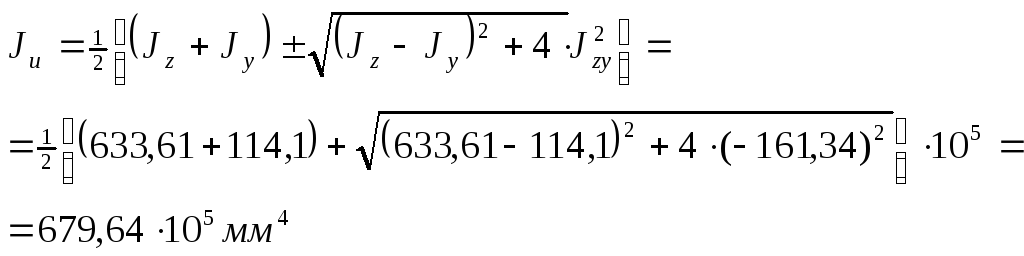
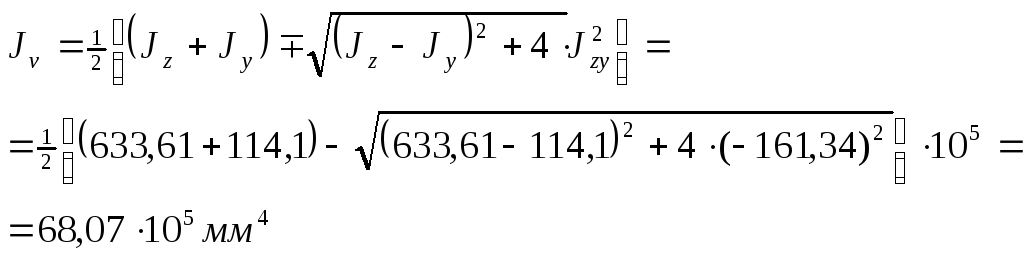
Т. к. >, принимаются верхние знаки:

Главные центральные радиусы инерции

мм;

мм

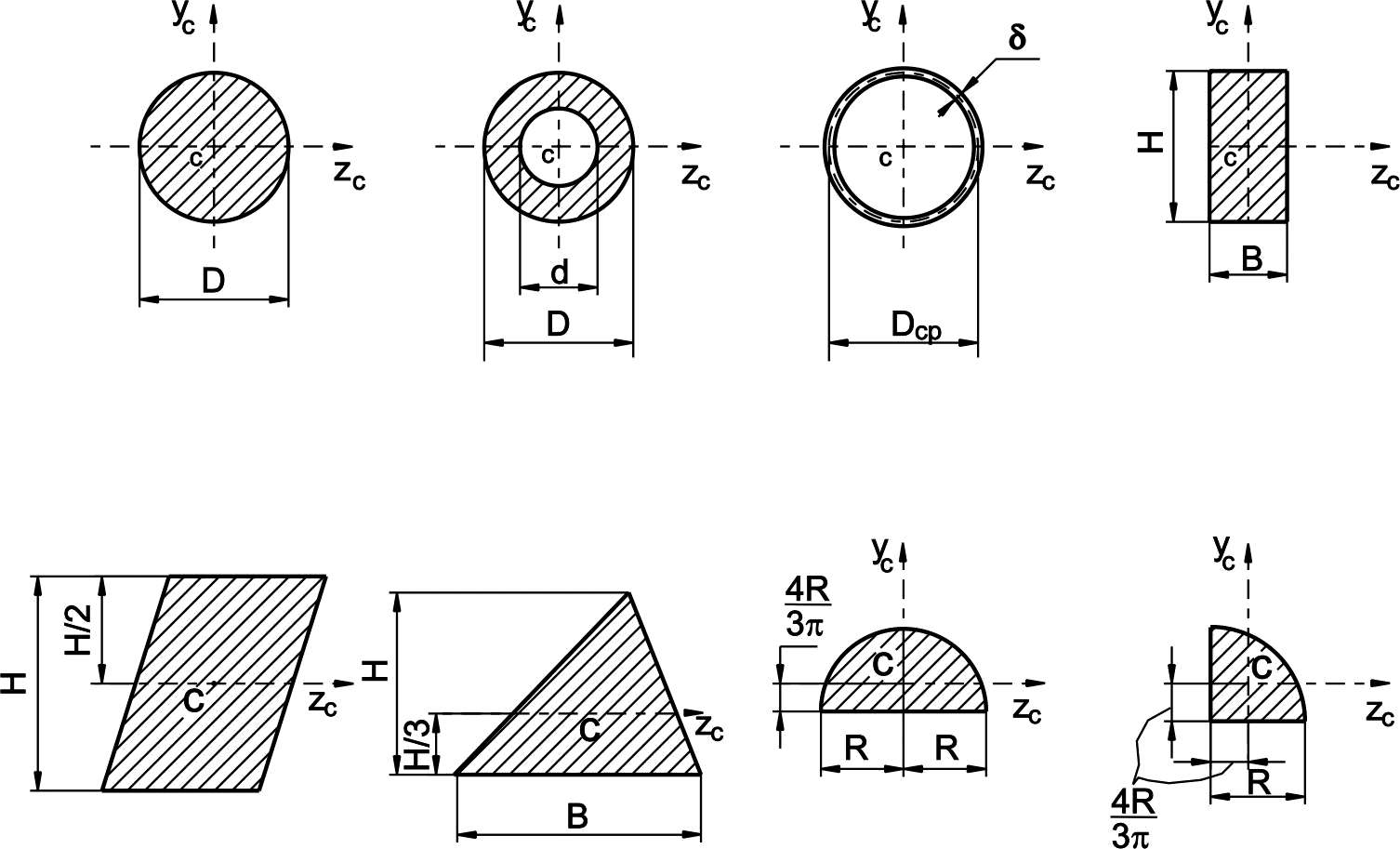
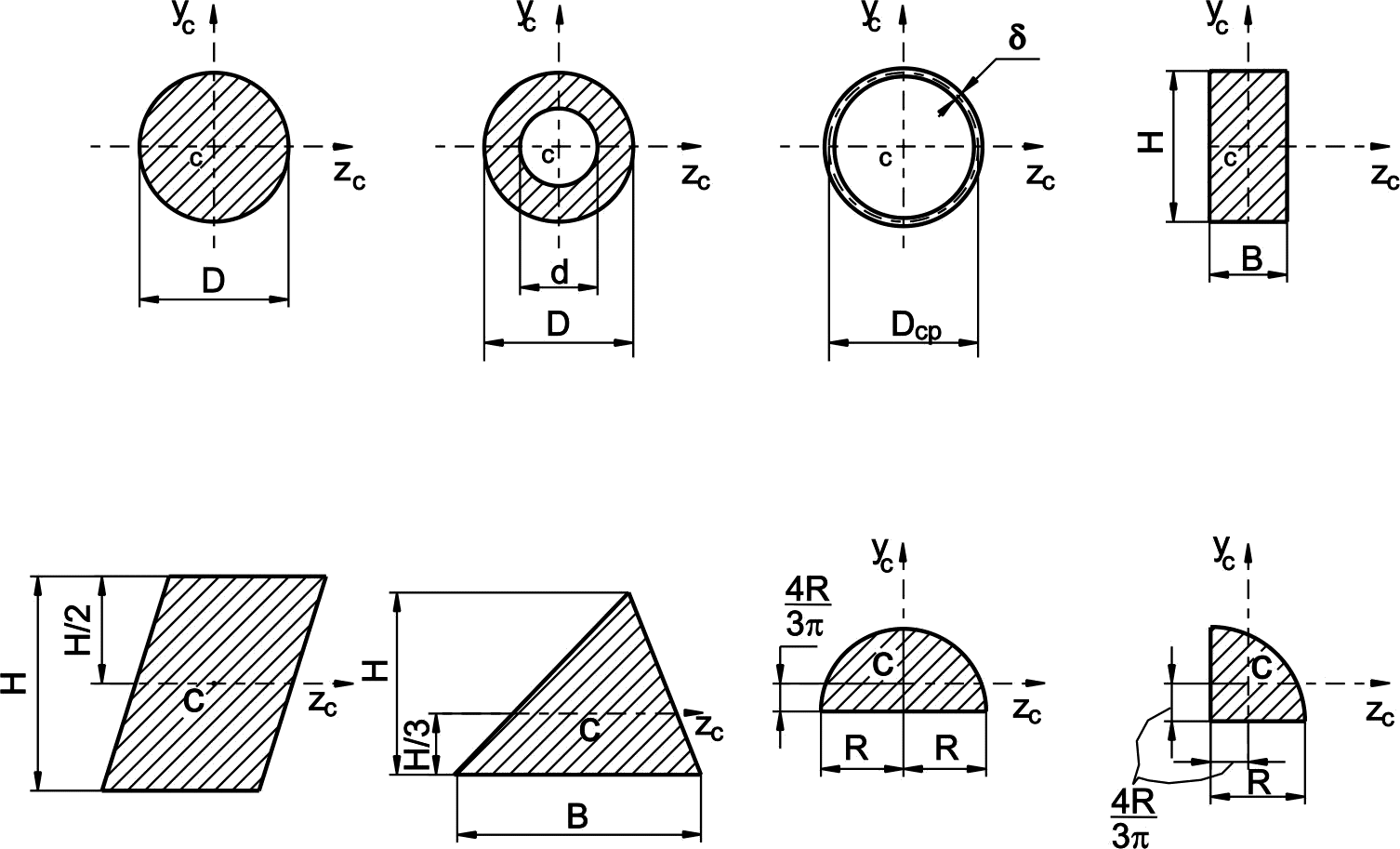
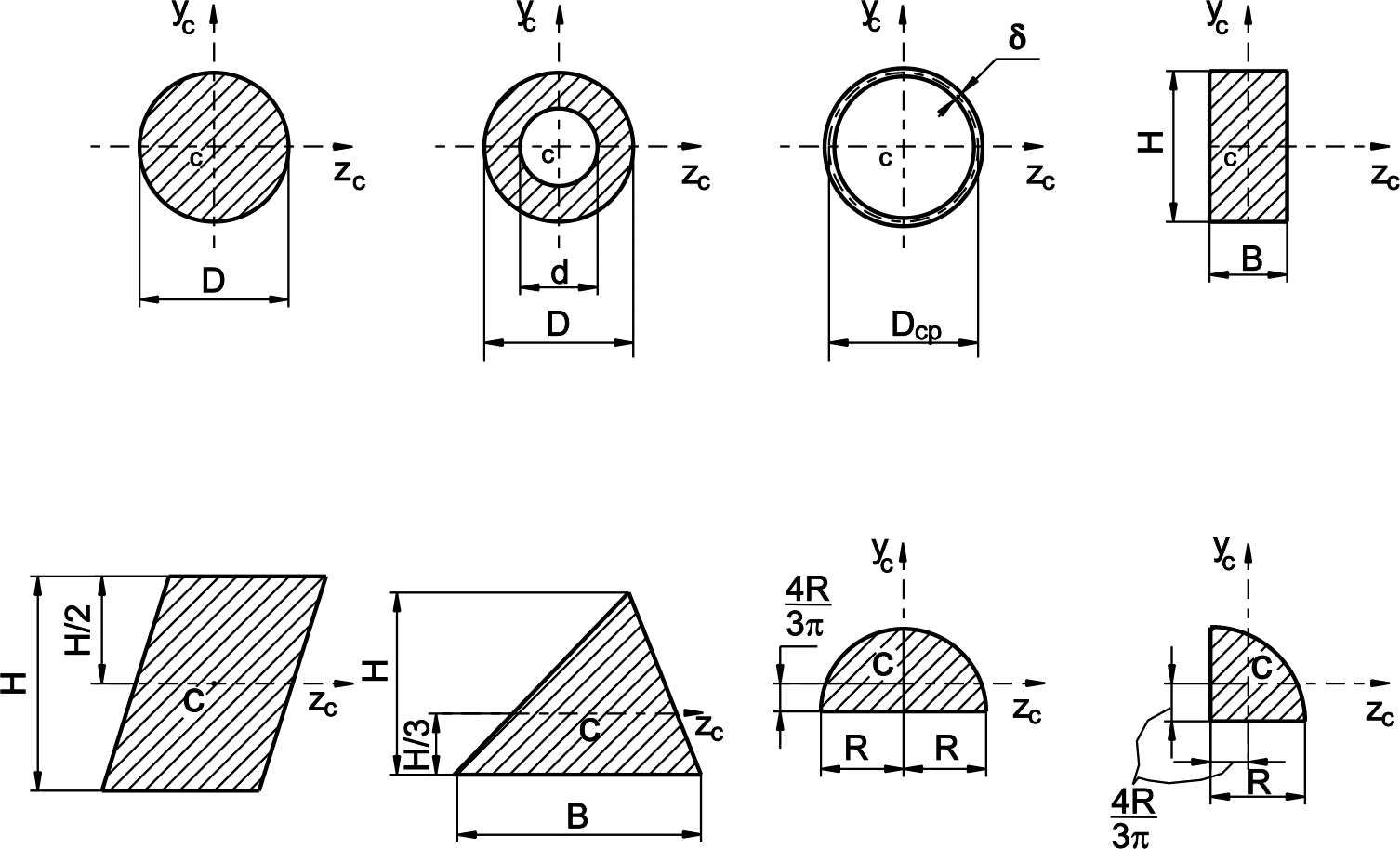
В таблице 1 приведены основные геометрические характеристики некоторых простых сечений с указанием расположения их центра тяжести.

Таблица 1

	;
	;

Литература

1 Писаренко Г.С. Сопротивление материалов. К: Вища школа. 1986.- 775с.