Laboratornaya_4
.pdf
Лабораторная работа №4.
ЧИСЛЕННОЕ РЕШЕНИЕ ЗАДАЧИ КОШИ ДЛЯ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
Постановка задачи Задача 1. Для обыкновенного дифференциального уравнения (ОДУ) первого порядка поставлена задача Коши:
du |
f t,u , t a, u a u0 |
, |
|
dt |
|||
|
|
f(t,u) - вектор правых частей (задан), u0- начальные данные (заданы). Требуется найти решение u(t) на отрезке [a,b].
Методы решения.
Введем по переменной t равномерную разностную сетку tn=a+n· , n=0,1,2,...M,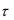 
b–a)/M
– шаг сетки. Вместо точного решения u(t) будем отыскивать приближенное решение yn,, заданное в узлах разностной сетки tn. Для определения yn используются конечноразностные методы. Простейшим является явный метод Эйлера, в котором уравнение заменяется разностной схемой:
yn 1 |
yn |
f tn , yn |
, n=0,1,2,..M–1. |
τ |
|
||
|
|
|
Решение определяется по формулам y0 =u0, yn+1=yn+ f(tn,yn); n=0,1,2,..M–1. Кроме того, могут быть использованы следующие методы:
1) Метод Рунге-Кутты 2-2 (двухшаговый, вариант 2, второго порядка аппроксимации)
k |
f x , y , k |
f x |
|
h |
, y |
|
h k |
|
|
|
|
||||||
1 |
i |
i |
2 |
|
|
i |
|
2 |
i |
2 |
1 |
|
|
|
|
||
|
yi 1 |
yi |
|
hk2 , i 0,1, 2,..., M |
|
|
|
|
|
||||||||
2) |
Метод Рунге-Кутты 3-1 (трехшаговый, вариант 1, третьего порядка аппроксимации) |
||||||||||||||||
k1 = f xi ,yi |
, k2 = f |
xi +h / 2,yi +hk1 / 2 , k3 |
f xi +h,yi - hk1+2hk2 |
|
|||||||||||||
|
|
|
|
y |
1 |
y |
|
h |
k 4k |
k , i 0,1, 2,..., M |
|
|
|||||
|
|
|
|
i |
i |
|
6 |
|
1 |
2 |
|
3 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3) |
Метод Рунге-Кутты 4-1 (четырехшаговый, вариант 1, четвертого порядка |
||||||||||||||||
аппроксимации) |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
k1 = f xi , yi |
, k2 = f |
xi +h / 2, yi +hk1 / 2 , k3 |
f xx +h / 2, yi +hk2 / 2 |
|
|||||||||||||
|
|
|
|
|
|
|
k4 |
|
f |
xi +h, yi +hk3 |
, |
|
|
||||
|
|
|
y |
y |
|
h k |
|
2k 2k |
k , i |
0,1, 2,..., M |
|
||||||
|
|
|
i 1 |
i |
|
6 |
1 |
|
2 |
|
3 |
4 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Формулировка задания |
|
|
|
|
|
|
|
|
|
|
|||||||
1. |
Для своего варианта проверить, |
что заданная функция u(t) является точным решением |
|||||||||||||||
|
и удовлетворяет начальным данным. |
|
|
|
|||||||||||||
2. |
Решить задачу Коши с помощью встроенного в MathCAD блока given/odesolve для |
||||||||||||||||
|
M = 10. Для каждого M включить в отчет следующую Таблицу: |
|
|||||||||||||||
Номер шага |
|
Значение |
|
|
Приближенное |
Точное решение |
Погрешность |
||||||||||
|
n |
|
|
|
аргумента tn |
|
|
|
решение yn |
u(tn) |
u(tn) - yn |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3. |
Составить программу решения задачи Коши методом Эйлера. Выполнить расчеты для |
||||||||||||||||
|
M = 10, |
20, 40. |
Сравнить |
полученное приближенное решение yn, |
n = 0,1,2,...,M, с |
||||||||||||
|
точным решением u(tn) в точках разностной сетки. Для каждого M вывести на экран |
||||||||||||||||
|
таблицу поведения приближенного решения и погрешности аналогичную таблице в |
||||||||||||||||
предыдущем пункте.
4.Составить программу решения задачи Коши методами Рунге-Кутты 1, 2, 3 и выполнить расчеты при различных М. Вывести на экран таблицы поведения решения и погрешности.
5.На отрезке [a, b] построить на экране функцию точного решения и вывести точки (tn,yn), соответствующие массивам приближенных решений, полученных методом Эйлера и каким-либо методом Рунге-Кутты для М = 10. Убедиться, что ломаная, соответствующая более точному методу, проходит ближе к графику точного решения, чем ломаная, полученная по методу первого порядка аппроксимации.
6.В отчет включить: постановку задачи, точное решение, описание методов приближенного решения, тексты программ, таблицу поведения максимальной
погрешности для методов Эйлера и Рунге-Кутты z max |
u tn |
yn |
, n = 0, 1,2,…M, для |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
разных M = 10, 20, 40, графики сравнения точного и приближенных решений. |
|||||||||||||||||||
|
|
|
Метод |
|
|
M |
|
|
|
|
|
Max погрешность u(tn) - yn |
|
||||||
|
|
|
|
|
|
|
|
|
|||||||||||
|
На основании поведения ошибки сделать вывод о порядке аппроксимации |
||||||||||||||||||
|
используемых методов. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Варианты заданий. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
du |
f |
t,u , t a,b , u |
a u0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
№ |
|
|
Правая часть |
|
|
Отрезок |
|
Начальные |
|
|
Точное решение |
||||||||
|
|
|
f(t,u) |
|
|
|
|
[a,b] |
|
данные u0 |
|
|
u(t) |
||||||
1. |
|
|
2t - u + t2 |
|
|
|
|
[ 0,2] |
|
|
0 |
|
|
|
t2 |
||||
2. |
|
|
Sin2(t) - u2 - Cos(t) |
|
|
[0, |
/ 2 ] |
|
|
0 |
|
|
-sin(t) |
||||||
3. |
|
0.5(cos2(t) u2) |
sin(t) |
|
|
[0, |
/ 2 ] |
|
|
1 |
|
|
cos(t) |
||||||
4. |
|
|
3t - 0.5 t u + t3 |
|
|
|
[0,2] |
|
|
-2 |
|
|
2(t2-1) |
||||||
5. |
|
|
t [2 + t2 sin(t2)-usin(u)] |
|
|
|
[-2,0] |
|
|
4 |
|
|
|
t2 |
|||||
6. |
|
|
(t + 1)(cos(t)–u)-sin(t) |
|
[ |
/2,3 |
/2] |
|
|
0 |
|
|
cos(t) |
||||||
7. |
|
|
u/t - 8/t2 |
|
|
|
|
[1,3] |
|
|
4 |
|
|
|
4/t |
||||
8. |
|
|
0.5(sin2(t) - u2)+cos(t) |
|
|
|
[0, |
/2] |
|
|
0 |
|
|
sin(t) |
|||||
9. |
|
|
cos2(t) - u2 - sin(t) |
|
|
|
[0, |
|
/2] |
|
|
1 |
|
|
cos(t) |
||||
10. |
|
|
3t3 - u2 + t6 |
|
|
|
|
[0,2] |
|
|
0 |
|
|
|
t3 |
||||
11. |
|
|
cos2(t) - u2/4 - 2 sin(t) |
|
|
|
[0, |
|
/2] |
|
|
2 |
|
|
2cos(t) |
||||
12. |
|
|
(t+0.6)(cos(t)–u)-sin(t) |
|
|
[ |
/2,3 |
/2] |
|
0 |
|
|
cos(t) |
||||||
13. |
|
|
(t+1) (sin(t)– u)+cos(t) |
|
|
[ |
/2,3 |
/2] |
|
1 |
|
|
sin (t) |
||||||
14. |
|
|
2(t – 2) + t (t - 2)2 – t u |
|
|
|
[2,4] |
|
|
0 |
|
|
(t-2)2 |
||||||
15. |
|
|
u/t –4/t4 |
|
|
|
|
[1,3] |
|
|
0 |
|
|
|
2/t |
||||
16. |
|
|
2t - u2 + t4 |
|
|
|
|
[0,2] |
|
|
0 |
|
|
|
t2 |
||||
17. |
|
|
Sin2(t) - u2 - Cos(t) |
|
|
[0, |
/ 2 ] |
|
|
0 |
|
|
-sin(t) |
||||||
18. |
|
0.5(cos2(t) u2) |
sin(t) |
|
|
[0, |
/ 2 ] |
|
|
1 |
|
|
cos(t) |
||||||
19. |
|
|
2t - u + t2 |
|
|
|
|
[ 0,2] |
|
|
0 |
|
|
|
t2 |
||||
20. |
|
|
(t + 1)(cos(t)–u)-sin(t) |
|
[ |
/2,3 |
/2] |
|
|
0 |
|
|
cos(t) |
||||||
21. |
|
|
u/t - 8/t2 |
|
|
|
|
[1,3] |
|
|
4 |
|
|
|
4/t |
||||
22. |
|
|
3t3 - u2 + t6 |
|
|
|
|
[0,2] |
|
|
0 |
|
|
|
t3 |
||||
23. |
|
|
cos2(t) - u2/4 - 2 sin(t) |
|
|
|
[0, |
|
/2] |
|
|
2 |
|
|
2cos(t) |
||||
24. |
|
|
(t+0.6)(cos(t)–u)-sin(t) |
|
|
[ |
/2,3 |
/2] |
|
0 |
|
|
cos(t) |
||||||
25. |
|
|
(t+1) (sin(t)– u)+cos(t) |
|
|
[ |
/2,3 |
/2] |
|
1 |
|
|
sin (t) |
||||||
26. |
|
|
2(t – 2) + t (t - 2)2 – t u |
|
|
|
[2,4] |
|
|
0 |
|
|
(t-2)2 |
||||||