Добавил:

ip Работы могут быть с косяками, тем не менее все были сданы на хорошо и отлично... т.ч. пользуйтесь, глядите чем то и помогут. Кроме того содержатся указания по работе некоторых преподавателей, в не сортированном материале Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Новосибирский государственный архитектурно-строительный университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

ИДЗ 4.1 КОМПЕНСАТОР_СО

.pdf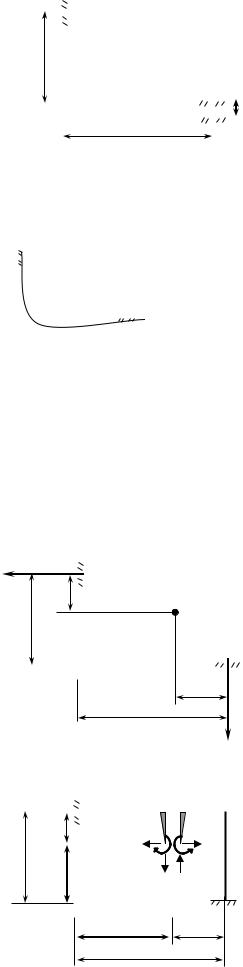

Скачиваний:

Добавлен:

27.06.2017

Размер:

467.21 Кб

Скачать

☆

Расчет компенсатора трубопровода при смещении опор методом сил

Дано:

EI 50кНм2 .

4м

Требуется:

1) построить эпюры внутренних усилий;

0, 2м

2) найти опорные реакции;

6м

3) проверить прочность трубопровода.

Решение

1)Найдем степень статической неопределимости

Это можно сделать с помощью формулы nst=3K-H, где K – количество замкнутых контуров системы, H – число простых шарниров.


	один			nst=3K-H=3∙1-0=3 - задача три раза статически неопределимая.
	один
	замкнутый
	замкнутый			Для раскрытия статической неопределимости
	контур			Для раскрытия статической неопределимости
				воспользуемся методом сил.
				воспользуемся методом сил.

2)Выберем основную систему метода сил

Основной системой метода сил (ОСМС) называют систему, образованную из заданной удалением лишних связей, если удалить все лишние связи, то ОСМС будет статически определимой системой. В данном случае рациональнее всего провести разрез компенсатора, получив, таким образом, два статически определимых стержня. Разрез лучше проводить так, чтобы он совпал с упругим центром системы (центром тяжести). Усилия в месте разреза обозначают x1, x2, x3 (неизвестные метода сил), причем располагают эти неизвестные в упругом центре на условных невесомых бесконечно жестких консолях. Все вышесказанное продемонстрировано ниже.

Р1 6 / EI

Найдем положение упругого центра системы.

Для этого назначим систему координат, в которой

0,8м

упругий центр

будем искать координаты центра тяжести системы.

4м

Р2

4 / EI

Sу.в.

x y

x ц.т.

, y ц.т.

,где Sу.в. , Sу.в. -

1,8м

6м

Тогда

координаты

x ц.т.

P1 3 P2 0

(6 / EI ) 3 0

P1 P2

6 / EI 4 / EI

0,8м

x 2

4м

x 3

3,2м

x 1

4, 2м	1,8м
6м

		статический момент упругих весов Р относительно
y			осей x и y соответственно, упругий вес стержня
			длиной l, находят с помощью формулы P l / EI .
			упругого		центра			составят
	18		1,8м, y ц.т.	P1 0 P2 2		0 (4 / EI ) 2	8	0,8м.
				P1 P2
	10					6 / EI 4 / EI 10

Основная система метода сил для жёсткой одноконтурной рамы с переносом неизвестных в упругий центр представлена слева. Кинематический анализ систем.

Очевидно, что обе вновь образованных системы являются геометрически неизменяемыми, т.к. крепятся к диску земля жесткой заделкой.

3) Система канонических уравнений метода сил

В настоящей задаче СКУМС имеет вид

11 x 1 12 x 2 13 x 3 1С 0

21 x 1 22 x 2 23 x 3 2С 0

31 x 1 32 x 2 33 x 3 3С 0

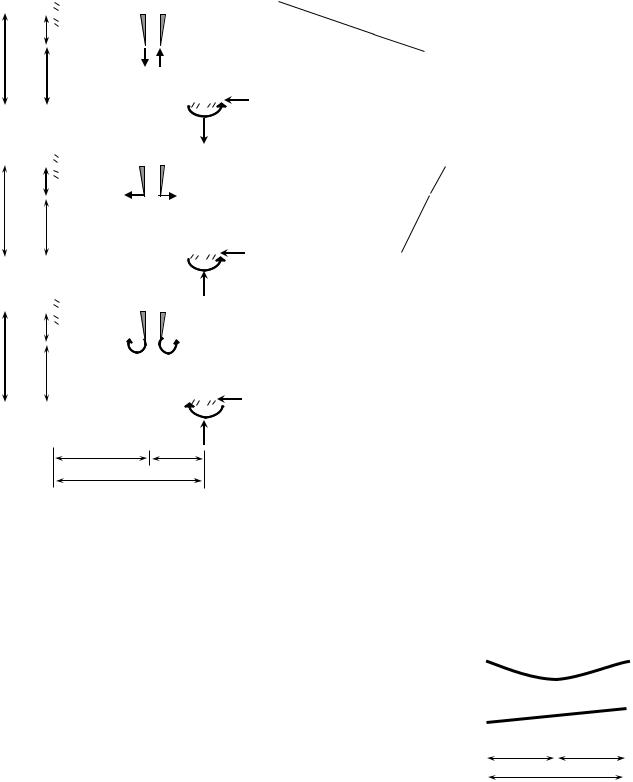
4)Построение эпюр моментов от единичных воздействий

Для ОСМС построим эпюры моментов от неизвестных x1=1, x2=1, x3=1, предварительно определив опорные реакции для опоры, имеющей смещение.

4, 2

Опорные реакции правой

0,8м

части (той опоры, которая

4м

x 1 1

1,8

сместилась) находят из

уравнений статики.

3,2м

Э п. M 1

Эпюры моментов

1 1,8

1,8

для левого стержня

строят как в консольной

0,8

балке не определяя

0,8м

x 2 1

реакции опор.

4м

Э п. M 2

1, 2

x 2 1

3,2м

3, 2

3,2

4м

0,8м

x 3 1

Э п. M 3

3,2м

4, 2м

1,8м 0

6м

5)Определение свободных членов канонических уравнений

В данном случае это перемещения в ОСМС по направлению неизвестных от смещения опор iС RnCn , здесь Rn - реакции в ОСМС от x1=1, x2=1, x3=1, Cn

- заданные по условию задачи смещения опор. Произведение RnCn положительно в том случае, когда направление смещения опорной связи и опорной реакции одинаковы.

1С (1 0,2 0 0) 0,2 ; 2С (0 1 0 0) 0; 3С (0 0 0) 0

6) Определение коэффициентов системы уравнений

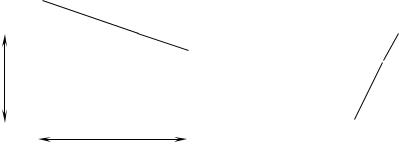
Перемещения

по направлению

неизвестных

от самих

неизвестных

ОСМС находят

с помощью

следующих

зависимостей

l / 2

(ab 4kf cd ) ,

6EI

		22				M 22															l
											ds													(ab 4kf cd ) ,
							EI				ds								6EI					(ab 4kf cd ) ,
				l
		33					M32							ds									l		(ab 4kf cd ),																							12 21																	M1M 2							ds							l		(ab 4kf cd ) ,
		33						EI						ds						6EI					(ab 4kf cd ),																							12 21																			EI					ds						6EI			(ab 4kf cd ) ,
				l																																																											l
	13 31															M1M3							ds								l				(ab 4kf cd ) , 23																					32										M2 M3							ds							l	(ab 4kf cd ) .
	13 31																EI						ds						6EI						(ab 4kf cd ) , 23																					32												EI					ds						6EI		(ab 4kf cd ) .
										l																																																						l
					4, 2																		1,2														1,8				0,8																									0,8						1												1	1



		4м																																														Э п. M 2												1, 2
																Э п. M 1																1,8																																																Э п. M 3						1







																																																								3, 2

																							6м






11						M12															6											2								2							2	4											2										2							2		39,6					,
												ds												(4, 2										4 1, 2							1,8							)					(1,8								4 1,8										1,8						)						,
							EI					ds							6EI					(4, 2										4 1, 2							1,8							)			6EI		(1,8								4 1,8										1,8						)				EI
				l
	22				M 22														6											2								2							2					4						2											2							2					14,933			,
						EI ds 6EI (0,8																												4 0,8					0,8							) 6EI (0,8												4 1, 2										3, 2							)					EI		,
						EI ds 6EI (0,8																												4 0,8					0,8							) 6EI (0,8												4 1, 2										3, 2							)					EI
				l
33						M32															6						2							2					2							4			2					2						2							10			,
							EI ds												6EI (1 4 1 1 ) 6EI (1 4 1 1 )																																																EI			,
							EI ds												6EI (1 4 1 1 ) 6EI (1 4 1 1 )																																																EI
				l
		12 21																M1M 2								ds								6			(4, 2 0,8 4 1, 2																	0,8 1,8 0,8)

																			EI																6EI
																l
	4		( 1,8 0,8 4 1,8 1, 2 1,8 3, 2)																																														14, 4			,
			( 1,8 0,8 4 1,8 1, 2 1,8 3, 2)																																																	,
		6EI																																																EI
	13		31										M1M3								ds						6						(4,2 1 4 1,2 1 1,8 1)																									4			( 1,8 1 4 1,8 1 1,8 1) 0 ,
	13		31													EI					ds						6EI						(4,2 1 4 1,2 1 1,8 1)																						6EI						( 1,8 1 4 1,8 1 1,8 1) 0 ,
									l
	23 32														M2 M3							ds								6				(0,8 1 4 0,8 1 0,8 1)																								4				(0,8					1 4 1,2 1 3,2 1) 0 .
	23 32															EI						ds						6EI						(0,8 1 4 0,8 1 0,8 1)																							6EI					(0,8					1 4 1,2 1 3,2 1) 0 .
										l
7) Определение неизвестных (x1, x2, x3) метода сил
Решим СКУ МС
																										39,6									x 1	14, 4								x 2 0 x 3 0, 2
																																																												0
																												EI										EI																						0
																												EI										EI
																										14, 4										14,933
																										14, 4								x 1		14,933									x 2 0 x 3									0
																																																												0
																												EI											EI																					0
																												EI											EI
																										0 x 1 0 x 2																10			x 3 0 0
																										0 x 1 0 x 2																			x 3 0 0
																																											EI
																																											EI

39, 6		x 1	14, 4		x		0, 2		0
						2
	EI			EI		2
	EI			EI
14, 4			14, 933
14, 4			14, 933
		x 1				x		2 0	0
	EI	x 1		EI		x		2 0	0
	EI			EI
x 3 0


39, 6		x 1	14, 4		x 2		0, 2		0

	EI			EI						EI 50
14, 4			14,933							EI 50
14, 4			14,933
		x 1				x		2 0	0
	EI	x 1		EI		x		2 0	0
	EI			EI
	39, 6x 1 14, 4x 2 10 0
	14, 4x 1 14,933x 2 0
	14, 4x 1 14,933x 2 0

x 1 0,3889;

Неизвестные: x 2 0,375;

x 3 0.

Проверка: 39,6 0,3889 14,4 ( 0,375) 10 15,4 15,4 0 14,4 0,3889 14,933( 0,375) 5,6002 5,5999 0,0003 0.

Знак «-» указывает на то, что усилие x2 направлено в другую сторону.

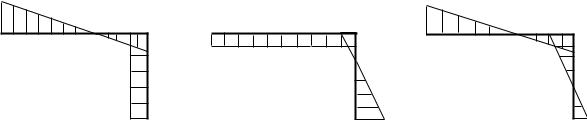
8)Построение эпюры моментов от смещения опор

Для этого воспользуемся принципом суперпозиции: МС=М1x1+М2x2+М3x3, предварительно получив эпюры Мixi при x1=0,3889; x2=-0,375; x3=0.

1,6334		0,3	1,3334	0,1667	1
		0,3			1
0,7	0,3		0,3		1
0,7	0,3				1
Э п. M1 x1		Э п. M2 x2		Э п. M C [кНм]
0,7			1, 2		0,5

9)Кинематическая проверка

Эпюра моментов от смещения опор поочередно сопрягается с эпюрами моментов от единичных воздействий, в результате должны получиться свободные члены с противоположными знаками ( 1С, 2С, 3С ), допустима невязка 5%.

1 ( X 1 , X 2 , X 3 )						M 1 M C								6			4
												d s				(4,2 1,3334 4 1,2 0,1667 1,8 1)				(1,8 1 4 1,8 0,25 1,8 0,5)
							E I					d s			6 E I	(4,2 1,3334 4 1,2 0,1667 1,8 1)		6E I		(1,8 1 4 1,8 0,25 1,8 0,5)
				l
	8,6032		1,8		10,4032						0,208 м; 1 С						0,2 м н ев я з к а с ос т а в л я е т					0,208 0,2		100 % 4% < 5% .
											0,208 м; 1 С						0,2 м н ев я з к а с ос т а в л я е т					0,2		100 % 4% < 5% .
	E I		E I				50															0,2
	2 ( X 1 , X 2 , X 3 )								M 2 M C							6	4
														d s			(0,8 1,3334 4 0,8 0,1667 0,8 1)						( 0,8 1 4 1, 0, 25 3, 2 0,5)
										E I				d s		6 E I	(0,8 1,3334 4 0,8 0,1667 0,8 1)				6E I		( 0,8 1 4 1, 0, 25 3, 2 0,5)
							l
		1,60016		1,6				0,0016					; 2 С 0 м				н ев я з к а с о с т а в л я е т		0,0016			100 % 1% < 5% .
				E I									; 2 С 0 м				н ев я з к а с о с т а в л я е т					100 % 1% < 5% .
		E I		E I						E I							1,6008

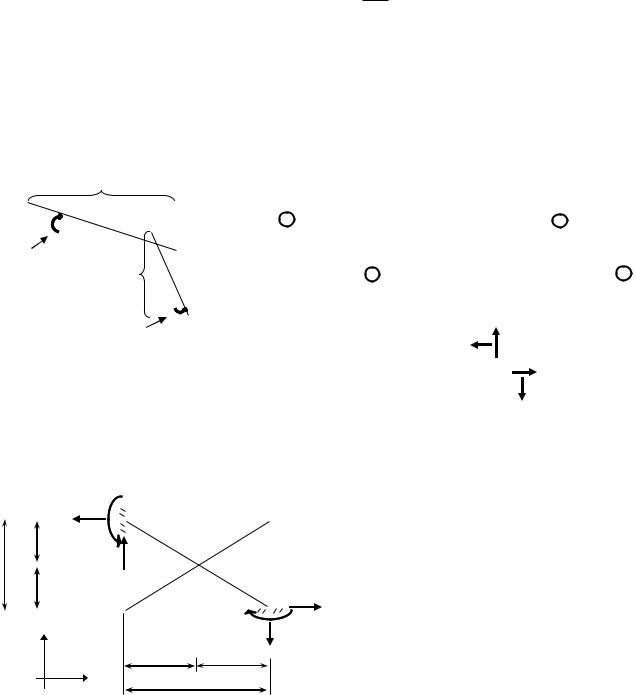
3 ( X 1 , X 2

, X 3 )

M 3 M C

d s

(11,3334 4 1 0,1667 11)

(11 4 1 0, 25 1 0,5)

6 E I

E I

6E I

1,0002

0,0002

; 3 С 0 м

н е в я з к а с о с т а в л я е т

0,0002

100 % 0,02 % < 5% .

E I

1,0001

10) Построение эпюр поперечных и продольных сил

Эпюру поперечных сил строят, опираясь на эпюру моментов. Значения поперечной силы на грузовых участках в данном случае находят только как

первую производную от функции моментов dMds Q tg . На эпюре моментов

представлены величины угла α, определив значения tgα, получим значения поперечной силы на I и II грузовых участках.

Для построения эпюры продольных сил используют метод вырезания узлов. С расчетной схемы берут сосредоточенные в узле силы (в настоящей задаче отсутствуют), с эпюры поперечных сил - значения внутренних усилий, все это переносят в узел и уравновешивают их значениями продольной силы (находят из уравнений статики).

1,3334		I			0,1667			1			0,3889					0,3889				0,375	0,375		0,375
1,3334					0,1667

" "									1														0,3889


													Э п. Q С [кН]									Э п. N С [кН]
	Э п. M C [кНм] II																			0,375


						" "				0,5											0,3889		0,3889
										0,5
									II
																					0,375
																					0,375
QI = tgαI =				1 1,3334			0,3889кН				, QII = tgαII =					1 0,5			0,375кН		0,3889		0,375
																							0,375


																	4
			6														4
11) Определение опорных реакций. Проверка равновесия системы
		0,375кН																			∑Fx=0; 0,35-0,375=0;
		0,375кН																			∑Fx=0; 0,35-0,375=0;
																					∑Fy=0; 0,3889-0,38890;
	2м 1,3334кНм																				∑Fy=0; 0,3889-0,38890;
	2м 1,3334кНм						0,3889кН					O						∑mо=0; 0,5+0,3889∙6-1,3334-0,375∙4=
4м							0,3889кН											∑mо=0; 0,5+0,3889∙6-1,3334-0,375∙4=
4м																					=2,834-2,834=0.
	2м																				=2,834-2,834=0.
	2м														0,375кН				Система находится в равновесии.
															0,375кН				Система находится в равновесии.

										0,5кНм				0,3889кН
			y							0,5кНм

x 3м 3м 6м

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
27.06.20171.21 Mб8Занятие 8-ACAD 10 word 3.doc
#
27.06.20171.54 Mб7Занятие 9 -ACAD 10 word 3.doc
#
27.06.2017605.33 Кб7ИДЗ 1 Многопролётная балка.pdf
#
27.06.2017326.09 Кб6ИДЗ 2 Расчёт ферм.pdf
#
27.06.2017522.81 Кб7ИДЗ 3 Статически неопределимая рама методом сил.pdf
#
27.06.2017467.21 Кб5ИДЗ 4.1 КОМПЕНСАТОР_СО.pdf
#
27.06.2017443.52 Кб5ИДЗ 4.2 КОМПЕНСАТОР_Т.pdf
#
27.06.20171.54 Mб7Лекции.pdf
#
27.06.2017605.33 Кб1Многопролётная.pdf
#
27.06.201723.44 Кб2Окно.docx
#
27.06.201770.44 Кб2ПланЖилогоПомещДляЗан14.dwg