4

22. . Формула Стокса

Для сферичес­кого тела (шарик) зависимость силы сопротивления при его движе­нии в сосуде с жидкостью от перечисленных выше факторов выра­жается законом Стокса:

F тр = 6π n r v (где r — радиус шарика; v — скорость движения. Этот закон полу­чен в предположении, что стенки сосуда не влияют на движение тела.

Для определения вязкости по методу Стокса берут высокий цилиндрический сосуд с исследуемой жидкостью. На сосуде имеются две кольцевые метки А и В. Метка А соответствует той высоте, где силы, действующие на шарик, уравновешивают друг друга и движение становится равномерным. Нижняя метка В нанесена для удобства отсчета времени. Бросая шарик в сосуд, отмечают по секундомеру время t прохождения шариком расстояния l между метками. Так как v = l/t то формула принимает вид

n = , где d- диаметр шарика.

23. метод Оствальда.

Медицинский вискозиметр используется для определения вяз­кости крови. Принцип его действия основан на том, что скорости продвижения жидкостей в капиллярах с одинаковыми сечениями при равных температурах и давлениях зависят от вязкости этих жидкостей.

Медицинский вискозиметр состоит из двух одинаковых гра­дуированных капилляров A1 и А2 . В капилляр A1 набирают определенный объем дистиллированной воды и пере­крывают кран Б. Это позволяет набрать в капилляр А иссле­дуемую жидкость, не изменяя уровень воды. Если теперь, открыв кран Б, создать разрежение в вискозиметре, то перемещение одной из жидкостей за одно и то же время будет обратно пропорцио­нально их вязкости:

n/n₀ = l₀/l или n = n₀l₀/l

где n — вязкость исследуемой жидкости; n₀— вязкость воды. Если вязкость воды принять равной единице, а путь, прой­денный жидкостью, составляет одно деление вискозиметра, то на основании вязкость жидкости численно равна пути, пройденному при этом водой.

24. Формула Пуазейля

Закон Пуазёйля  — это физический закон так называемого течения Пуазёйля, то есть установившегося течения вязкой несжимаемой жидкости в тонкой цилиндрической трубке Где p1-p2 — перепад давления на концах капилляра, Па;Q— секундный объёмный расход жидкости, м³/с,R— радиус капилляра, м;d — диаметр капилляра, м;ŋ— коэффициент динамической вязкости, Па·с;l — длина трубы, м.

Гидравлическое сопротивление - сопротивление движению жидкостей (и газов), оказываемое трубопроводом. Х = 8ηl / (πR⁴)

25. Последовательность соединения трубок.

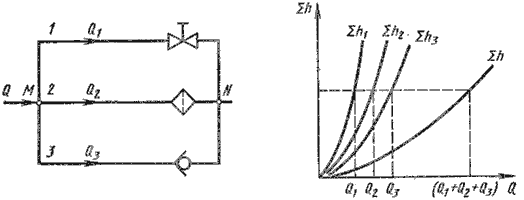
Гидравлическое сопротивление тем больше, чем больше вязкость n, длина l трубы и меньше площадь поперечного сечения. Аналогия между электрическим и гидравлическим сопротивлениями позволя­ет в некоторых случаях использовать правило нахождения электри­ческого сопротивления последовательного и параллельного соедине­ний проводника для определения гидравлического сопротивления системы последовательно или параллельно соединенных труб. Так, например, общее гидравлическое сопротивление трех труб, соеди­ненных последовательно и параллельно вычисляется по формулам

X=X₁+X₂+X₃

X= [1/X₁ + 1/X₂+1/X₃]^-1

^{Параллельное соединение трубок}

Обозначим полные напоры в точках М и N соответственно HM и HN , расход в основной магистрали через Q, а в параллельных трубопроводах через Q1, Q2 и Q3; суммарные потери в этих трубопроводах через Σ1 , Σ2 и Σ3.Очевидно, что расход жидкости в основной магистрали

Q = Q1 = Q2 = Q3, Σh1 = HM - HN; Σh2 = HM - HN;Σh3 = HM – HN, Σh1 = Σh2 = Σh3

т.е. потери напора в параллельных трубопроводах равны между собой

26. ПОВЕРХНОСТНОЕ НАТЯЖЕНИЕ

На поверхностях раздела жидкости и ее насыщенного пара, двух несмешиваемых жидкостей, жидкости и твердого тела возникает сила, обусловленная различным межмолекулярным взаимодействи¬ем граничащих сред.

Поверхностное натяжение определяется отношением работы, затраченной на создание некоторой поверхности жидкости при постоянной температуре к площади этой поверхности: σ =А/S Поверхностное натяжение зависит от температуры. Вдали от критической температуры значение его убывает линейно при увеличении температуры. Снижения поверхностного натяжения можно достигнуть введением в жидкость поверхностно-активных веществ, уменьшающих энергию поверхностного слоя.

Коэффициент пропорциональности  — сила, приходящаяся на единицу длины контура — называется коэффициентом поверхностного натяжения. Он измеряется в ньютонах на метр.

Если σ32> σ13 ,т.е. силы взаимодействия между молекулами жидкости и твердого тела больше, чем между молеку-лами твердого тела и газа, то θ < π/2 и жидкость смачивает твер¬дое тело, поверхность которого в этом случае называется гидрофиль¬ной. В случае σ32< σ13θ > π/2, жидкость не смачивает тела, поверхность его в этом случае называют гидрофобной. Капиллярные явления определяют условия конденсации паров, кипения жидкостей, кристаллизации и т.п. Так, например, на молекулу пара над вогнутым мениском жидкос¬ти действует больше молекул жидкости и, следовательно, большая сила, чем при выпуклом мениске.

27. Закон Гука . Модуль Юнга. Модуль упругости.

Закон Гу́ка — уравнение теории упругости, связывающее напряжение и деформацию упругой среды. Сила упругости, возникающая в теле при его деформации, прямо пропорциональна величине этой деформации

Для тонкого растяжимого стержня закон Гука имеет вид: F=K▲L

Коэффициент упругости зависит как от свойств материала, так и от размеров стержня. Можно выделить зависимость от размеров стержня (площади поперечного сеченияS и длины L) явно, записав коэффициент упругости как

k=Величина E называется модулем упругости первого рода или модулем Юнга и является механической характеристикой материала..Также при расчёте прямых стержней применяют запись закона Гука в относительной форме

▲L= Следует иметь в виду, что закон Гука выполняется только при малых деформациях. При превышении предела пропорциональности связь между напряжениями и деформациями становится нелинейной. Для многих сред закон Гука неприменим даже при малых деформациях.

28. Закон Ома для переменного тока

Сдвиг по фазе между током и напряжением обозначается углом φ. Индуктивное сопротивление (реактивное) обозначается X, активное сопротивление — R, кажущееся сопротивление цепи или проводника — Z. Полное сопротивление (импеданс) вычисляется по формуле:

Где:Z - полное сопротивление, ОмR - активное сопротивление, Ом

Закон Ома для цепи переменного тока :

U=I*Z

где:U - напряжение или разность потенциалов,I — сила тока,Z = Re−iδ — комплексное сопротивление (импеданс),R = (Ra2 + Rr2)1/2 — полное сопротивление,Rr = ωL − 1/(ωC) — реактивное сопротивление (разность индуктивного и емкостного),Rа — активное (омическое) сопротивление, не зависящее от частоты,δ = − arctg (Rr/Ra) — сдвиг фаз между напряжением и силой тока.

Реактивное сопротивление – это сопротивление катушек индуктивности (дросселей) и конденсаторов. Величина реактивного сопротивления уже зависит от частоты тока. Так на постоянном токе реактивное сопротивление конденсатора устремляется к бесконечности, а дросселя наоборот – к нулю (без учета активной составляющей сопротивления провода).

С изменением частоты тока электрическое сопротивление конденсатора изменяется, по закону:

Xc = 1/2pfC2,где Xc – сопротивление, Ом; f – частота, Гц; С – емкость, Ф.

Реактивное сопротивление катушки индуктивности с увеличением частоты возрастает:

XL = 2pfL,где XL – сопротивление катушки, Ом; f – частота, Гц; L – индуктивность, Гн.

29/ Полное сопротивление. Зависимость импеданса…

импеданс –

полное электрическое сопротивление цепи переменному току

Полная цепь переменного тока - это цепь из генератора, а также R, C, и L

элементов, взятых в разных сочетаниях и количествах. Для разбора проходящих в электрических цепях процессов используют полные последовательные и параллельные цепи. Последовательная цепь - это такая цепь, где все элементы могут быть соединены последовательно, один за другим. В параллельной цепи R, C, L элементы соединены параллельно

Особенности полной цепи:

1.Соблюдается закон Ома

2.Полная цепь оказывает переменному току сопротивление. Это сопротивление

называется полным (мнимым, кажущимся) или импедансом.

3.Импеданс зависит от сопротивления всех элементов цепи, обозначается Z и

вычисляется не простым, а геометрическим (векторным) суммированием. Для

последовательно соединенных элементов формула импеданса имеет следующее

значение:

здесь:

Z - импеданс последовательной цепи,

R - активное сопротивление,

XL – индуктивное и XC – ёмкостное сопротивление,

L - индуктивность катушки (генри),

C - ёмкость конденсатора (фарад).

импеданс изменяется с изменением частоты

тока, на котором проводится измерение: при увеличении частоты реактивная составляющая импеданса уменьшается. Зависимость импеданса от частоты тока называется дисперсией импеданса.

Изменение импеданса с частотой обусловлено также зависимостью поляризации от периода Т переменного тока. Если время, в течение которого

электрическое поле направлено в одну сторону (Т/2), больше времени релаксации τ какого-либо вида поляризации, то поляризация достигает своего наибольшего значения, и до тех пор, пока T/2>τ, эффективная диэлектрическая проницаемость и проводимость объекта не будут изменяться с частотой. Если же при увеличении частоты полупериод T/2 переменного тока становится меньше времени релаксации, то поляризация не успевает достигнуть своего максимального значения. После этого диэлектрическая проницаемость начинает

уменьшаться с частотой, а проводимость - возрастать.