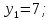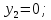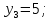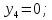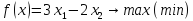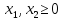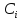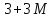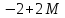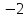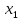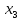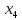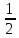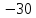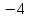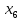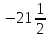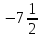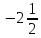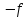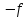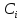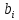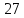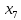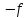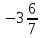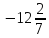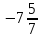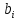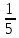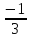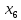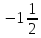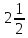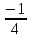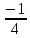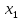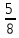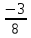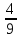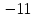Министерство образования и науки Российской Федерации
Государственное образовательное учреждение
Высшего образования
Новосибирский Государственный Технический Университет
Контрольная работа
По курсу: «Математические методы исследования экономики и математическое программирование»
Факультет: ИДО
Группа: ЭКз-41
Студент: Кражич Владимир Бранимирович
Преподаватель:
Вариант:
Дата сдачи работы:
Отметка о защите:
Новосибирск, 2017
Оглавление
Задание № 1 4
Задание №2 6
Задание №3 10
Задание №4 21
Задание № 1
Дано:
|
|
|
|
|
|
Решение:
Для построения первого опорного плана систему неравенств необходимо привести к системе уравнений путем введения переменных, таким образом мы произведем переход к канонической форме.
В
первом неравенстве вводим базисную
переменную
,
во втором неравенстве вводим базисные
переменные
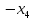и
,
в третьем неравенстве вводим базисную
переменную
,
в четвертом неравенстве вводим базисную
переменную
.
Получим следующее
|
№ |
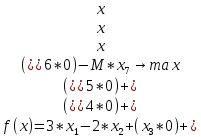
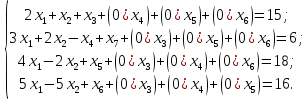
Базис |
|
Решение
|
3 |
|
0 |
0 |
0 |
0 |
|
|
|
|
|
|
|
|
| ||||
|
0 |
|
0 |
15 |
2 |
1 |
1 |
0 |
0 |
0 |
0 |
|
|
|
6 |
3 |
2 |
0 |
|
0 |
0 |
1 | |
|
|
0 |
18 |
4 |
-2 |
0 |
0 |
1 |
0 |
0 | |
|
|
0 |
16 |
5 |
-5 |
0 |
0 |
0 |
1 |
0 | |
|
|
|
|
|
|
0 |
|
0 |
0 |
0 |
Текущий опорный план не оптимален, так как в индексной строке находятся отрицательные коэффициенты.
В
качестве ведущего выберем столбец,
соответствующий переменной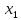
,
так как это наибольший коэффициент по
модулю.
Вычислим
значения
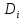по строкам как частное от деления
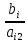и выберем наименьшее из них:
.
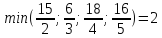Следовательно, вторая строка является ведущей.
Разрешающий элемент находится на пересечении ведущего столбца и ведущей строки и равен 3. Получаем новую симплекс-таблицу:
|
№ |
Базис |
|
Решение
|
3 |
|
0 |
0 |
0 |
0 |
|
|
|
|
|
|
| ||||
|
1 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
3 |
|
1 |
|
|
0 |
0 |
0 | |
|
|
0 |
|
14 |
2 |
|
0 |
0 |
1 | |
|
|
0 |
|
0 |
|
|
0 |
0 |
1 | |
|
|
|
|
0 |
|
|
0 |
0 |
0 |
В
последней симплекс-таблице в строке
симплекс-разности все значения
.
Ответ:
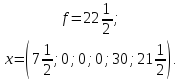
Задание №2
Дано:
|
Вид сырья |
Товар |
Запас сырья | ||||
|
1 |
2 |
3 |
4 | |||
|
1 |
5 |
4 |
6 |
7 |
275 | |
|
2 |
2 |
0 |
4 |
2 |
100 | |
|
3 |
3 |
2 |
0 |
1 |
85 | |
|
Прибыль |
50 |
27 |
34 |
54 |
| |
Решение:
Для
начала определим максимальное значение
целевой функции
,
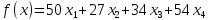при следующих ограничивающих условиях:
|
№ |
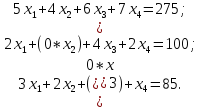
Базис |
|
Решение
|
50 |
|
34 |
54 |
0 |
0 |
|
|
|
|
|
|
|
|
| ||||
|
0 |
|
0 |
275 |
5 |
4 |
6 |
7 |
1 |
0 |
0 |
|
|
|
100 |
2 |
0 |
4 |
2 |
0 |
1 |
0 | |
|
|
0 |
85 |
3 |
2 |
0 |
1 |
0 |
0 |
1 | |
|
|
|
|
50 |
27 |
34 |
54 |
0 |
0 |
0 |
Выбираем
наибольшую положительную симплекс-разность
(ту, которая определит ведущий столбец),
а для того чтобы определить ведущую
строку, вычисляем неотрицательное
отношение
.
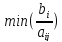Получаем новую симплекс-таблицу:
|
№ |
Базис |
|
Решение
|
50 |
|
34 |
54 |
0 |
0 |
|
|
|
|
|
|
|
|
| ||||
|
1 |
|
54 |
|
|
|
|
1 |
|
0 |
0 |
|
|
|
|
|
|
|
0 |
|
1 |
0 | |
|
|
0 |
|
|
|
|
0 |
|
0 |
1 | |
|
|
|
|
|
|
|
0 |
|
0 |
0 |
Повторно
выбираем наибольшую положительную
симплекс-разность (ту, которая определит
ведущий столбец), а для того чтобы
определить ведущую строку, вычисляем
неотрицательное отношение
.
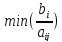Получаем новую симплекс-таблицу:
|
№ |
Базис |
|
Решение
|
50 |
|
34 |
54 |
0 |
0 |
|
|
|
|
|
|
|
|
| ||||
|
2 |
|
54 |
25 |
0 |
|
|
1 |
|
0 |
|
|
|
0 |
10 |
0 |
|
|
0 |
|
1 |
| |
|
|
50 |
20 |
1 |
|
|
0 |
0 |
0 |
| |
|
|
|
|
0 |
|
|
0 |
|
0 |
|
В
последней симплекс-таблице в строке
симплекс-разности все значения
.
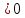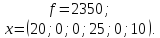
Решим двойственную задачу:
.
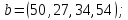
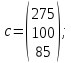
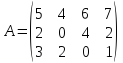Транспонируем матрицу:
.
Имеем следующее:
;
;
;
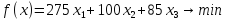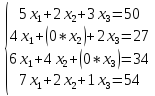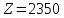