
Вариант 8 эконометрика
.docxВариант 1
Задания:
|
x |
y |
|
0,11 |
15 |
|
0,19 |
10,3 |
|
0,2 |
4,5 |
|
0,15 |
-0,5 |
|
0,05 |
-4,5 |
|
0,05 |
2,9 |
|
0,16 |
14,2 |
|
0,06 |
4,6 |
|
0,12 |
13,6 |
|
0,08 |
0,9 |
|
0,05 |
2,4 |
|
0,09 |
11,8 |
|
0,15 |
6,3 |
|
0,11 |
-0,7 |
|
0,05 |
5,6 |
|
0,11 |
7,7 |
|
0,02 |
3 |
|
0,01 |
-4,1 |
|
0,14 |
-1 |
|
0,16 |
1,6 |
|
0,11 |
11,8 |
|
0,01 |
-3,9 |
|
0,07 |
13,6 |
|
0,15 |
2,7 |
|
0,08 |
1,2 |
|
0,04 |
-7,6 |
|
0,04 |
3,5 |
|
0,05 |
9,2 |
|
0,2 |
6,2 |
|
0,08 |
11,8 |
|
0,11 |
2,2 |
|
0,13 |
12,5 |
|
0,09 |
1,3 |
|
0,01 |
-3,4 |
|
0,13 |
18,4 |
|
0,2 |
10,1 |
|
0,17 |
18,2 |
|
0,1 |
3,8 |
|
0,15 |
0,8 |
|
0,15 |
9,9 |
|
0,17 |
4,8 |
|
0,13 |
5 |
|
0,16 |
6,4 |
|
0,11 |
10,2 |
|
0,16 |
9,2 |
2) Определите параметры уравнения парной линейной и степенной регрессии. Дайте интерпретацию найденных параметров и всего уравнения в целом.
3) Постройте теоретическую линию регрессии, совместив ее с полем корреляции. Сделайте выводы.
4) Рассчитайте линейный коэффициент корреляции и поясните его смысл. Определите коэффициент детерминации и дайте его интерпретацию.
5) Оцените статистическую значимость коэффициентов регрессии и уравнения регрессии в целом и постройте доверительные интервалы для точных значений параметров с уровнем значимости 0,05. Сделайте выводы.
Решение:
1.Построим поле корреляции результативного и факторного признаков.
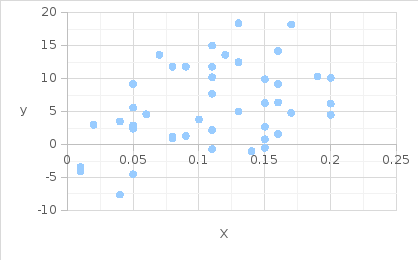
Рис. Поле корреляции
По итогам построенного поля корреляции можно сделать вывод, что между признаками наблюдается обратная заметная корреляционная связь, так как значения сконцентрированы вдоль воображаемой нисходящей линии.
2. Определим параметры уравнения парной линейной и степенной регрессии.
Уравнение линейной регрессии имеет
вид:
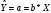 .
.
Для определения параметров уравнения а и b построим вспомогательную таблицу.
|
x |
y |
x2 |
y2 |
xy |
yтеор |
(y-yср)2 |
(y-yтеор)2 |
(х-хср)2 |
|
0,11 |
15 |
0,0121 |
225 |
1,65 |
5,69 |
88,569 |
86,727 |
0,000 |
|
0,19 |
10,3 |
0,0361 |
106,09 |
1,957 |
9,62 |
22,195 |
0,458 |
0,007 |
|
0,2 |
4,5 |
0,04 |
20,25 |
0,9 |
10,12 |
1,186 |
31,533 |
0,008 |
|
0,15 |
-0,5 |
0,0225 |
0,25 |
-0,075 |
7,66 |
37,075 |
66,510 |
0,002 |
|
0,05 |
-4,5 |
0,0025 |
20,25 |
-0,225 |
2,74 |
101,786 |
52,348 |
0,003 |
|
0,05 |
2,9 |
0,0025 |
8,41 |
0,145 |
2,74 |
7,230 |
0,027 |
0,003 |
|
0,16 |
14,2 |
0,0256 |
201,64 |
2,272 |
8,15 |
74,151 |
36,634 |
0,003 |
|
0,06 |
4,6 |
0,0036 |
21,16 |
0,276 |
3,23 |
0,978 |
1,885 |
0,002 |
|
0,12 |
13,6 |
0,0144 |
184,96 |
1,632 |
6,18 |
64,178 |
55,067 |
0,000 |
|
0,08 |
0,9 |
0,0064 |
0,81 |
0,072 |
4,21 |
21,986 |
10,964 |
0,001 |
|
0,05 |
2,4 |
0,0025 |
5,76 |
0,12 |
2,74 |
10,169 |
0,112 |
0,003 |
|
0,09 |
11,8 |
0,0081 |
139,24 |
1,062 |
4,70 |
38,578 |
50,364 |
0,000 |
|
0,15 |
6,3 |
0,0225 |
39,69 |
0,945 |
7,66 |
0,506 |
1,837 |
0,002 |
|
0,11 |
-0,7 |
0,0121 |
0,49 |
-0,077 |
5,69 |
39,550 |
40,798 |
0,000 |
|
0,05 |
5,6 |
0,0025 |
31,36 |
0,28 |
2,74 |
0,000 |
8,207 |
0,003 |
|
0,11 |
7,7 |
0,0121 |
59,29 |
0,847 |
5,69 |
4,457 |
4,051 |
0,000 |
|
0,02 |
3 |
0,0004 |
9 |
0,06 |
1,26 |
6,702 |
3,031 |
0,008 |
|
0,01 |
-4,1 |
0,0001 |
16,81 |
-0,041 |
0,77 |
93,875 |
23,689 |
0,010 |
|
0,14 |
-1 |
0,0196 |
1 |
-0,14 |
7,16 |
43,413 |
66,640 |
0,001 |
|
0,16 |
1,6 |
0,0256 |
2,56 |
0,256 |
8,15 |
15,911 |
42,868 |
0,003 |
|
0,11 |
11,8 |
0,0121 |
139,24 |
1,298 |
5,69 |
38,578 |
37,365 |
0,000 |
|
0,01 |
-3,9 |
0,0001 |
15,21 |
-0,039 |
0,77 |
90,039 |
21,782 |
0,010 |
|
0,07 |
13,6 |
0,0049 |
184,96 |
0,952 |
3,72 |
64,178 |
97,630 |
0,001 |
|
0,15 |
2,7 |
0,0225 |
7,29 |
0,405 |
7,66 |
8,346 |
24,556 |
0,002 |
|
0,08 |
1,2 |
0,0064 |
1,44 |
0,096 |
4,21 |
19,262 |
9,068 |
0,001 |
|
0,04 |
-7,6 |
0,0016 |
57,76 |
-0,304 |
2,24 |
173,947 |
96,888 |
0,005 |
|
0,04 |
3,5 |
0,0016 |
12,25 |
0,14 |
2,24 |
4,363 |
1,580 |
0,005 |
|
0,05 |
9,2 |
0,0025 |
84,64 |
0,46 |
2,74 |
13,040 |
41,794 |
0,003 |
|
0,2 |
6,2 |
0,04 |
38,44 |
1,24 |
10,12 |
0,373 |
15,331 |
0,008 |
|
0,08 |
11,8 |
0,0064 |
139,24 |
0,944 |
4,21 |
38,578 |
57,589 |
0,001 |
|
0,11 |
2,2 |
0,0121 |
4,84 |
0,242 |
5,69 |
11,485 |
12,161 |
0,000 |
|
0,13 |
12,5 |
0,0169 |
156,25 |
1,625 |
6,67 |
47,763 |
33,973 |
0,000 |
|
0,09 |
1,3 |
0,0081 |
1,69 |
0,117 |
4,70 |
18,395 |
11,582 |
0,000 |
|
0,01 |
-3,4 |
0,0001 |
11,56 |
-0,034 |
0,77 |
80,800 |
17,365 |
0,010 |
|
0,13 |
18,4 |
0,0169 |
338,56 |
2,392 |
6,67 |
164,125 |
137,562 |
0,000 |
|
0,2 |
10,1 |
0,04 |
102,01 |
2,02 |
10,12 |
20,350 |
0,000 |
0,008 |
|
0,17 |
18,2 |
0,0289 |
331,24 |
3,094 |
8,64 |
159,040 |
91,405 |
0,004 |
|
0,1 |
3,8 |
0,01 |
14,44 |
0,38 |
5,20 |
3,200 |
1,947 |
0,000 |
|
0,15 |
0,8 |
0,0225 |
0,64 |
0,12 |
7,66 |
22,933 |
46,996 |
0,002 |
|
0,15 |
9,9 |
0,0225 |
98,01 |
1,485 |
7,66 |
18,586 |
5,038 |
0,002 |
|
0,17 |
4,8 |
0,0289 |
23,04 |
0,816 |
8,64 |
0,622 |
14,741 |
0,004 |
|
0,13 |
5 |
0,0169 |
25 |
0,65 |
6,67 |
0,347 |
2,793 |
0,000 |
|
0,16 |
6,4 |
0,0256 |
40,96 |
1,024 |
8,15 |
0,658 |
3,053 |
0,003 |
|
0,11 |
10,2 |
0,0121 |
104,04 |
1,122 |
5,69 |
21,262 |
20,365 |
0,000 |
|
0,16 |
9,2 |
0,0256 |
84,64 |
1,472 |
8,15 |
13,040 |
1,108 |
0,003 |
|
∑=4,86 |
∑=251,5 |
∑=0,6564 |
∑=3111,41 |
∑=33,633 |
∑=251,5 |
∑=1705,804 |
∑=1387,421 |
∑=0,132 |
Получаем:
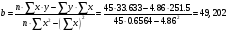 ;
;
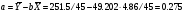 .
.
Уравнение линейной регрессии имеет
вид:
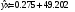 .
.
Таким образом, с ростом факторного признака на единицу результативный признак возрастает на 49,202 единиц.
Уравнение степенной модели имеет вид:
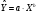 .
.
Для построения этой модели необходимо
произвести линеаризацию переменных.
Для этого произведем логарифмирование
обеих частей уравнения:
 .
.
Обозначим Y=ln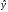 ,
Х=lnx, А=lna.
,
Х=lnx, А=lna.
Тогда уравнение имеет вид: Y=A+bX – линейное уравнение регрессии.
Построим вспомогательную таблицу.
|
x |
y |
Х |
Y |
Х2 |
Y2 |
XY |
yтеор |
(y-yтеор)2 |
|
0,11 |
15 |
-2,21 |
2,71 |
4,87 |
7,33 |
-5,98 |
4,67 |
106,62 |
|
0,19 |
10,3 |
-1,66 |
2,33 |
2,76 |
5,44 |
-3,87 |
6,39 |
15,30 |
|
0,2 |
4,5 |
-1,61 |
1,50 |
2,59 |
2,26 |
-2,42 |
6,58 |
4,32 |
|
0,15 |
-0,5 |
-1,90 |
0,00 |
3,60 |
0,00 |
0,00 |
5,58 |
36,98 |
|
0,05 |
-4,5 |
-3,00 |
0,00 |
8,97 |
0,00 |
0,00 |
2,98 |
55,92 |
|
0,05 |
2,9 |
-3,00 |
1,06 |
8,97 |
1,13 |
-3,19 |
2,98 |
0,01 |
|
0,16 |
14,2 |
-1,83 |
2,65 |
3,36 |
7,04 |
-4,86 |
5,79 |
70,71 |
|
0,06 |
4,6 |
-2,81 |
1,53 |
7,92 |
2,33 |
-4,29 |
3,31 |
1,68 |
|
0,12 |
13,6 |
-2,12 |
2,61 |
4,50 |
6,81 |
-5,53 |
4,91 |
75,47 |
|
0,08 |
0,9 |
-2,53 |
-0,11 |
6,38 |
0,01 |
0,27 |
3,90 |
8,98 |
|
0,05 |
2,4 |
-3,00 |
0,88 |
8,97 |
0,77 |
-2,62 |
2,98 |
0,33 |
|
0,09 |
11,8 |
-2,41 |
2,47 |
5,80 |
6,09 |
-5,94 |
4,17 |
58,26 |
|
0,15 |
6,3 |
-1,90 |
1,84 |
3,60 |
3,39 |
-3,49 |
5,58 |
0,52 |
|
0,11 |
-0,7 |
-2,21 |
0,00 |
4,87 |
0,00 |
0,00 |
4,67 |
28,88 |
|
0,05 |
5,6 |
-3,00 |
1,72 |
8,97 |
2,97 |
-5,16 |
2,98 |
6,88 |
|
0,11 |
7,7 |
-2,21 |
2,04 |
4,87 |
4,17 |
-4,51 |
4,67 |
9,16 |
|
0,02 |
3 |
-3,91 |
1,10 |
15,30 |
1,21 |
-4,30 |
1,76 |
1,53 |
|
0,01 |
-4,1 |
-4,61 |
0,00 |
21,21 |
0,00 |
0,00 |
1,19 |
27,95 |
|
0,14 |
-1 |
-1,97 |
0,00 |
3,87 |
0,00 |
0,00 |
5,37 |
40,52 |
|
0,16 |
1,6 |
-1,83 |
0,47 |
3,36 |
0,22 |
-0,86 |
5,79 |
17,56 |
|
0,11 |
11,8 |
-2,21 |
2,47 |
4,87 |
6,09 |
-5,45 |
4,67 |
50,78 |
|
0,01 |
-3,9 |
-4,61 |
0,00 |
21,21 |
0,00 |
0,00 |
1,19 |
25,87 |
|
0,07 |
13,6 |
-2,66 |
2,61 |
7,07 |
6,81 |
-6,94 |
3,61 |
99,81 |
|
0,15 |
2,7 |
-1,90 |
0,99 |
3,60 |
0,99 |
-1,88 |
5,58 |
8,30 |
|
0,08 |
1,2 |
-2,53 |
0,18 |
6,38 |
0,03 |
-0,46 |
3,90 |
7,27 |
|
0,04 |
-7,6 |
-3,22 |
0,00 |
10,36 |
0,00 |
0,00 |
2,62 |
104,47 |
|
0,04 |
3,5 |
-3,22 |
1,25 |
10,36 |
1,57 |
-4,03 |
2,62 |
0,77 |
|
0,05 |
9,2 |
-3,00 |
2,22 |
8,97 |
4,92 |
-6,65 |
2,98 |
38,71 |
|
0,2 |
6,2 |
-1,61 |
1,82 |
2,59 |
3,33 |
-2,94 |
6,58 |
0,14 |
|
0,08 |
11,8 |
-2,53 |
2,47 |
6,38 |
6,09 |
-6,23 |
3,90 |
62,47 |
|
0,11 |
2,2 |
-2,21 |
0,79 |
4,87 |
0,62 |
-1,74 |
4,67 |
6,12 |
|
0,13 |
12,5 |
-2,04 |
2,53 |
4,16 |
6,38 |
-5,15 |
5,14 |
54,13 |
|
0,09 |
1,3 |
-2,41 |
0,26 |
5,80 |
0,07 |
-0,63 |
4,17 |
8,22 |
|
0,01 |
-3,4 |
-4,61 |
0,00 |
21,21 |
0,00 |
0,00 |
1,19 |
21,04 |
|
0,13 |
18,4 |
-2,04 |
2,91 |
4,16 |
8,48 |
-5,94 |
5,14 |
175,76 |
|
0,2 |
10,1 |
-1,61 |
2,31 |
2,59 |
5,35 |
-3,72 |
6,58 |
12,40 |
|
0,17 |
18,2 |
-1,77 |
2,90 |
3,14 |
8,42 |
-5,14 |
6,00 |
148,96 |
|
0,1 |
3,8 |
-2,30 |
1,34 |
5,30 |
1,78 |
-3,07 |
4,43 |
0,39 |
|
0,15 |
0,8 |
-1,90 |
-0,22 |
3,60 |
0,05 |
0,42 |
5,58 |
22,86 |
|
0,15 |
9,9 |
-1,90 |
2,29 |
3,60 |
5,26 |
-4,35 |
5,58 |
18,65 |
|
0,17 |
4,8 |
-1,77 |
1,57 |
3,14 |
2,46 |
-2,78 |
6,00 |
1,43 |
|
0,13 |
5 |
-2,04 |
1,61 |
4,16 |
2,59 |
-3,28 |
5,14 |
0,02 |
|
0,16 |
6,4 |
-1,83 |
1,86 |
3,36 |
3,45 |
-3,40 |
5,79 |
0,37 |
|
0,11 |
10,2 |
-2,21 |
2,32 |
4,87 |
5,39 |
-5,13 |
4,67 |
30,54 |
|
0,16 |
9,2 |
-1,83 |
2,22 |
3,36 |
4,92 |
-4,07 |
5,79 |
11,62 |
|
∑=4,86 |
∑=251,5 |
∑=-109,61 |
∑=63,51 |
∑=293,86 |
∑=136,23 |
∑=-139,34 |
∑=199,75 |
∑=1478,67 |
