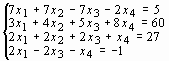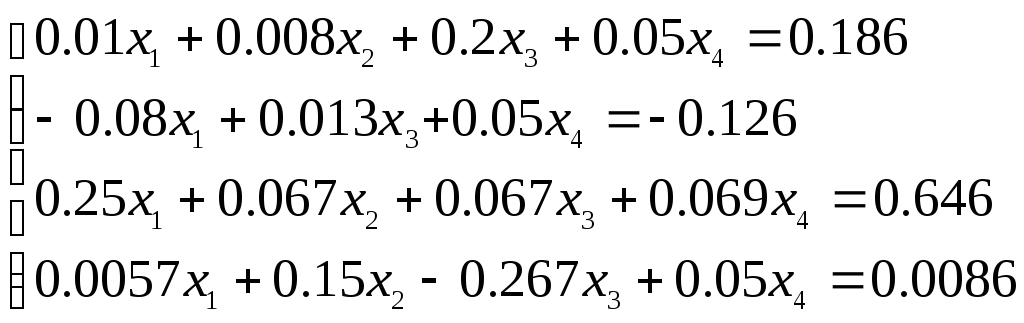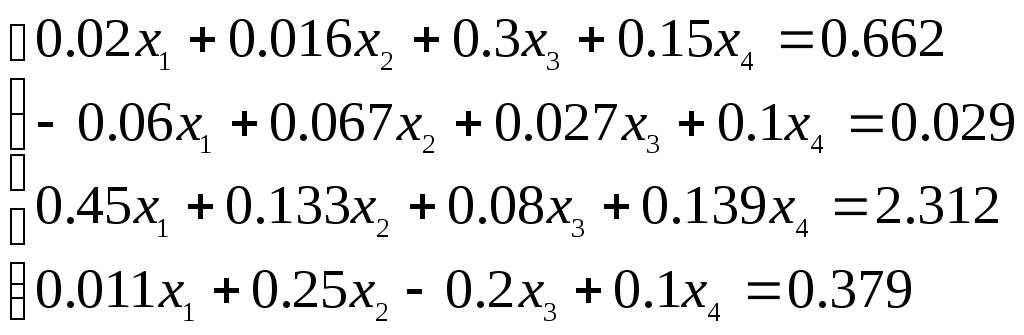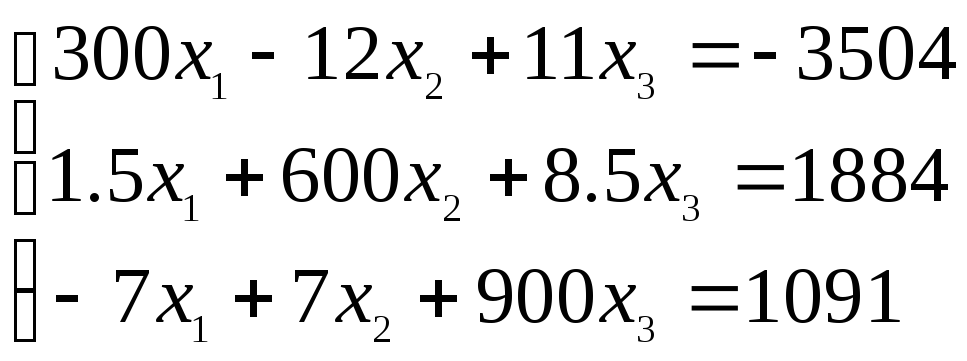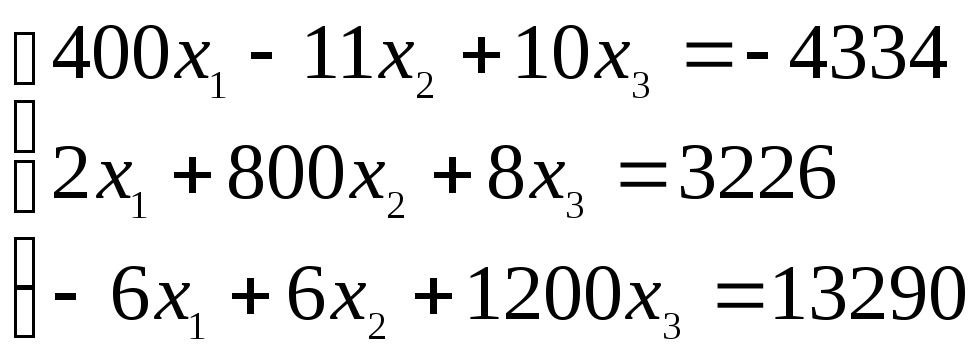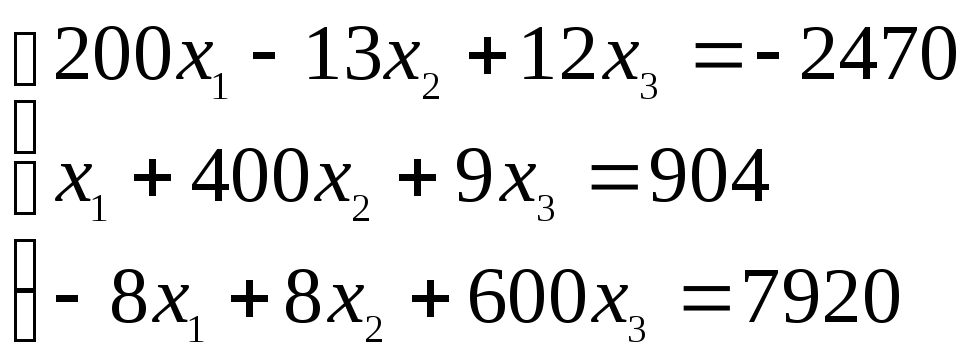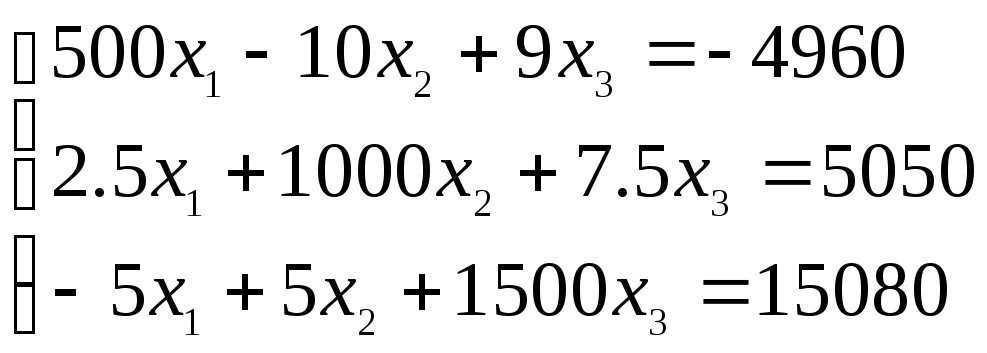Mathcad №3

Системы линейных алгебраических уравнений

Решение матричных уравнений

В задачах линейной алгебры практически всегда возникает не­обходимость выполнять различные операции с матрицами. Предва­рительно матрицу нужно определить и ввести в рабочий документ Mathcad. Для того чтобы определить матрицу, необходимо ввести с клавиатуры имя матрицы и знак присваивания. Затем щелкнуть по кнопке в панели математических инструментов, чтобы открыть панель операций с ма­трицами и векторами (рис.1).

Рис.1

Далее нужно щелчком по кнопке открыть окно диалога Вставить матрицу, определить число строк и число столбцов, а затем щелкнуть по кнопке ОК.

В рабочем документе справа от знака присваивания откроется поле ввода матрицы с помеченными позициями для ввода элементов.

Функции, предназначенные для решения задач линейной алгебры, можно разделить на три группы: функции определения матриц и операции с блоками матриц, функции вычисления различных числовых характеристик матриц и функции, реализующие численные алгоритмы решения задач линейной алгебры. Опишем наиболее часто используемые функции.

Функции определения матриц и операции с блоками ма­триц:

diag(v) - создает диагональную матрицу, элементы главной диагонали которой хранятся в векторе v;

identity(n) — создает единичную матрицу порядка n;

augment(A, В) — формирует матрицу, в первых столбцах которой содержится матрица А, а в последних — матрица В (матрицы А и B должны иметь одинаковое число строк);

stack(A, В) — формирует матрицу, в первых строках которой содержится матрица А, а в последних — матрица В (матрицы А и В должны иметь одинаковое число столбцов);

submatrix(A, ir, jr, ic, jc) — формирует матрицу, которая является блоком матрицы А, расположенным в строках с ir no jr и в столбцах с ic по jc, ir < jr, ic < jc.

Номер первой строки (столбца) матрицы или первой компоненты вектора хранится в Mathcad в переменной ORIGIN. По умолчанию в Mathcad координаты векторов, столбцы и строки матрицы нумеру­ются начиная с 0 (ORIGIN := 0). Поскольку в математической записи чаще используется нумерация с 1, то в дальнейшем перед началом работы с матрицами будем определять значение переменной ORIGIN равным 1, т.е. будем прежде всего выполнять команду ORIGIN := 1.

Фрагмент рабочего документа Mathcad, содержащий примеры исполнения перечисленных выше функций, приведен ниже.

Функции вычисления различных числовых характеристик матриц:

last(v) — вычисление номера последней компоненты вектора v;

length (v) — вычисление количества компонент вектора v;

rows(A) — вычисление числа строк в матрице А;

cols(A) — вычисление числа столбцов в матрице А;

mах(А) — вычисление наибольшего элемента в матрице А;

rank(A) — вычисление ранга матрицы А;

norm1(A), norm2(A), norme(A), normi(A) — вычисление норм квадратной матрицы А.

Примеры использования названных функций для матриц, определенных в приведенном ранее рабочем документе.

last(v) = 4 length(v) = 4

rows(D)=3 cols(D)=7 max(D)=5 rank(A) =2

norm1(B)=4

Функции, реализующие численные алгоритмы решении задач линейной алгебры:

rref(A) - приведение матрицы к ступенчатому виду с единичным базисным минором (выполняются элементарные операции со строками матрицы);

lsolve(A, b) — решение системы линейных алгебраических уравнений Ax=b.

Матричная форма записи линейных систем.

Рассмотрим систему n линейных алгебраических уравнений относительно n неизвестных x₁, x₂,…, x_n:

(1)

В соответствии с правилами умножения матриц рассмотренная система линейных уравнений может быть записана в матричном виде Ax = b, где

, ,

Матрица А называется матрицей системы; матрица-столбец b, элементами которой являются правые части уравнений системы, называется матрицей правой части. Матрица-столбец x, элементы которой – искомые неизвестные, называется решением системы.

Метод Крамера

Справедливо следующее утверждение. Если определитель  = det A матрицы системы Ax = b отличен от нуля, то система имеет единственное решение x₁, x₂,…, x_n, определяемое формулами Крамера , где _i – определитель матрицы n-го порядка, полученной из матрицы системы заменой i-го столбца столбцом правых частей.

Метод обратной матрицы

Если матрица системы невырождена (т.е. определитель отличен от нуля), то у нее существует обратная матрица и тогда решение системы имеет следующий вид: x = A^-1b.

Метод Гаусса

Метод Гаусса, его еще называют методом гауссовских исключений, состоит в том, что систему n линейных алгебраических уравнений относительно n неизвестных x₁, x₂,…, x_n (1) приводят последовательным исключением неизвестных к эквивалентной системе с треугольной матрицей

,

решение которой находят по рекуррентным формулам

В матричной записи это означает, что сначала (прямой ход метода Гаусса) элементарными операциями над строками приводят расширенную матрицу системы к ступенчатому виду:

,

а затем (обратный ход метода Гаусса) эту ступенчатую матрицу преобразуют так, чтобы в первых n столбцах получилась единичная матрица:

.

Последний, (n+1)-й столбец этой матрицы содержит решение системы.

В Mathcad прямой и обратный ходы метода Гаусса выполняет функция rref(A).

Метод простых итераций

Метод простых итераций (последовательных приближений) является одним из приближенных методов решения линейных алгебраических уравнений.

Итерационный процесс заключается в последовательном уточнении начального приближения х₀. Каждый такой шаг называется итерацией. В результате итераций находим последова­тельность приближенных значений корня х₁,х₂...х_n. Если с ростом n эти значения приближаются к истинному значению корня, то говорят, что итерационный процесс сходится.

Метод состоит в том, что система уравнений Cx = d преобразуется к виду x=b + Ax и ее решение вычисляется как предел последовательности

Для сходимости метода простых итераций достаточно, чтобы выполнялось условие по какой либо норме матрицы, согласованной с нормой векторов.

Понятие нормы позволяет оценить степень близости двух векторов. В частности, если норма разности точного и приближенного решений системы мала, то, по-видимому, приближенное решение хорошо аппроксимирует точное решение.

Задания:

Задание 1. Исследуйте и, если решение существует, найдите по формулам Крамера решение системы. (Таблица 1)

Порядок выполнения работы.

1. Присвойте переменной ORIGIN значение, равное единице.

2. Введите матрицу системы и столбец правых частей (A, b).

3. Вычислите определитель матрицы системы. Система имеет единственное решение, если определитель отличен от нуля.

Пример:

4. Вычислите определители матриц, полученных заменой соответствующего столбца столбцом правых частей (₁, ₂, ₃, ₄).

5. Найдите решение системы по формулам Крамера.

Задание 2. Решите систему линейных алгебраических уравнений (Таблица 1) методом обратной матрицы.

Порядок выполнения работы.

1. Ввести систему линейных уравнений. Например:

x+2y+3z=7

x-3y+2z=5

x+y+z=3

При записи уравнений используйте Булево равенство из панели Булевы операторы.

2. Введите матрицу системы и матрицу-столбец правых частей (A, b).

3. Вычислите решение системы по формуле x = A^-1b, (x=).

4. Проверьте правильность решения по формуле Ax – b.

5. Найдите решение системы с помощью функции lsolve и сравните результаты вычислений.

Задание 3. Найдите методом Гаусса решение системы линейных алгебраических уравнений. (Таблица 1)

Порядок выполнения работы.

1. Присвойте переменной ORIGIN значение, равное единице.

2. Введите матрицу системы и матрицу-столбец правых частей.

3. Сформируйте расширенную матрицу системы с помощью функции augment(A,B) и присвойте ей имя Ar.

4. Приведите расширенную матрицу системы к ступенчатому виду с помощью функции rref(A), где А – расширенная матрица системы. Присвойте ступенчатой матрице имя As.

5. Сформируйте столбец решения системы с помощью функции submatrix(A, ir, jr, ic, jc), где А – ступенчатая матрица.

6. Проверьте правильность решения по формуле Ax – b.

Варианты заданий 1, 2, 3

  Таблица 1

№ варианта	Система линейных уравнений	№ варианта	Система линейных уравнений
1		14
2		15
3		16
4		17
5		18
6		19
7		20
8		21
9		22
10		23
11		24
12		25
13		26

Варианты задания 4

  Таблица 2

№ варианта	Система линейных уравнений	№ варианта	Система линейных уравнений
1		14
2		15
3		16
4		17
5		18
6		19
7		20
8		21
9		22
10		23
11		24
12		25
13		26

9