Тригонометрическая и показательная формы записи комплексного числа
Тригонометрическая форма записи комплексного числа: z= (cos +isin )= ei- (формула Эйлера)- показательная форма записи комплексного числа.
Геометрическая интерпретация сложения
и умножения. Сложение двух комплексных
чисел можно рассматривать как сложение
двух векторов на плоскости. При этом
справедливы Неравенства треугольника
z1+z2
z1+z2;
z1-z2
z1-z2
z1-z2
- расстояние между z1 и z2 на
комплексной плоскости.
-окрестность точки z0: z-z0<,
0<z-z0<
- выколотая (проколотая)
-окрестность точки z0. При умножении
двух комплексных чисел их модули
перемножаются (растяжение или
сжатие), а аргументы складываются
(поворот на плоскости). z1=a1+i
b1= 1ei;
z2=a2+i b2=2ei;
z1 z2=12ei(
+ )
=> |z1z2|=|z1||z2|;
arg(z1 z2)=arg z1+ arg z2 .
При делении двух комплексных чисел
их модули делятся (модуль
знаменателя ╧ 0), а
аргументы вычитаются:
z1/z2=(1/2)ei(
- )
=> z1/z2|=|z1|/|z2|;
arg(z1/z2)=arg z1- arg z2
.Алгебраической формой записи комплексных
чисел удобно пользоваться при операциях
сложения и вычитания, а показательной-
при умножении, делении, возведении в
целую степень, извлечении целого корня
(возведение в рациональную степень).
Возведение в целую степень.
zn=[ (cos +isin )]n=[ ei ]=nein== n(cos(n )+isin(n ));
Формула Муавра: (cos +isin )n = cos(n )+isin(n ).
Пример:
(1+i)3=(
ei
/4)3=23/2
ei3
/4=23/2(cos(3
/4)+i sin(3
/4))=-2+2i ;
Извлечение целого корня (возведение в рациональную степень).
z= ei=
ei(
+2 k)
, k=0,
1,
2... . 
-
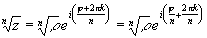
корень n-той степени из комплексного числа имеет n различных значений, котторые получаются при k=0, 1, 2...n-1.
Пример: 
=1
ei(0+2
k)/4={1 (k=0), i (k=1), -1 (k=2), -i
(k=3) }.