9. Геометрический и механический смысл производной.

Механическое значение производной.

Пусть дан путь S, пройденный поступательно движущимся телом, в зависимости от времени t выражается формулой .

Как уже известно, скорость V тела в данный момент равна первой производной от пути по времени .

Пусть в некоторый момент t скорость тела была равна V. Если движение не является равномерным, то за промежуток времени ∆t, истекший с момента t, скорость изменится и получится приращение ∆V.

Средним ускорением за время ∆t называется отношение приращения от скорости ∆V к приращению времени .

Ускорением в данный момент называется предел отношения скорости к приращению времени, когда последнее стремиться к нулю:

Иначе говоря, ускорение (в данный момент) равно производной от скорости по времени:

но так как , то, следовательно,

т.е. ускорение прямолинейного движения равно второй производной от пути по времени

10. Правило вычисления производной функции.

Для нахождения производной от данной функции , исходя из общего определения производной, необходимо произвести следующие действия:

1. Дать аргументу 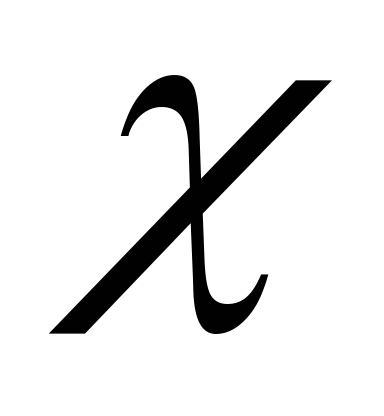приращение 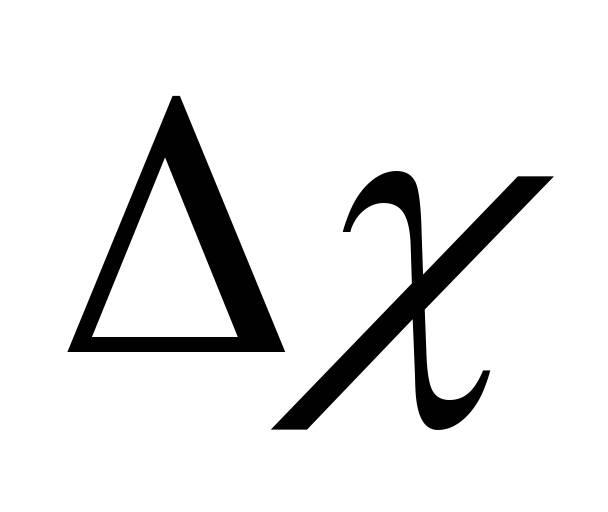, вычислить значение функции при этом

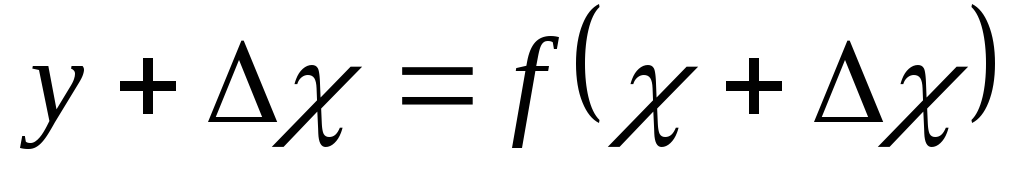
2. Найти соответствующее приращение функции

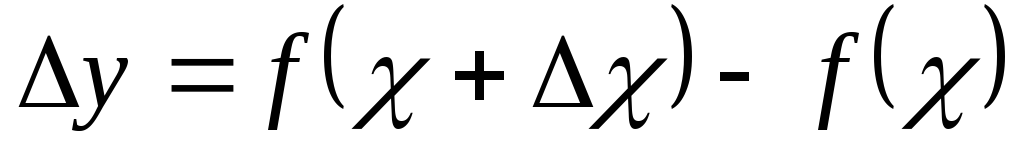
3. Составить отношение приращения функции к приращению аргумента: .

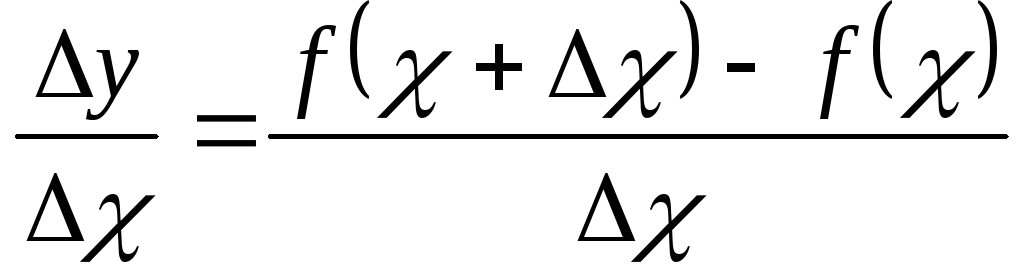4. Найти предел данного соотношения при

.

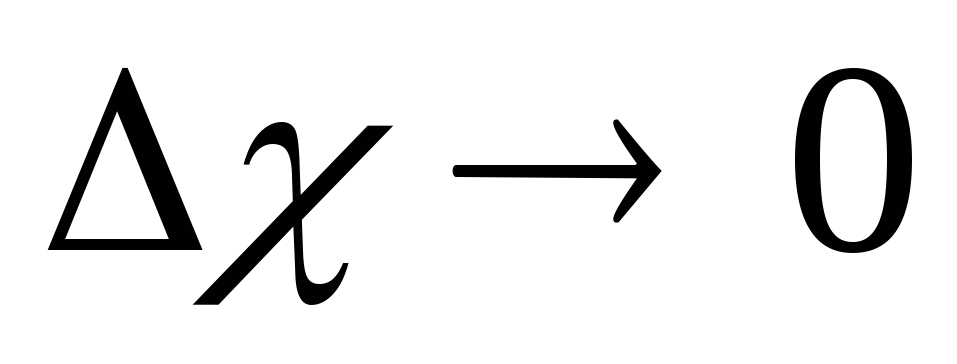
В дальнейшем мы будем применять этот общий способ для вычисления производных от некоторых элементарных функций.

Производная функции , где - целое положительное число, равна , то есть

Производная от есть , то есть

Производная от есть, то есть

Производная постоянной равна нулю, то есть , где , то .

Постоянный множитель можно выносить за знак производной, то есть если , где , то .

11. Производные суммы, разности, произведения и частного двух функций.

Производная суммы конечного числа дифференцируемых функций равна соответствующей сумме производных этих функций, то есть если

Производная от произведения двух дифференцируемых функций равна произведению первой функции на вторую плюс произведение первой функции на производную от второй, то есть

если , то

Производная дроби (т.е. частного от деления двух функций) равна дроби, у которой знаменатель есть квадрат знаменателя данной дроби, а числитель есть разность между произведением знаменателя на производную числителя и произведением числителя на производную знаменателя, то есть

если

12. Производная логарифмической, показательной и сложной функции.

Производная от функции , то есть если , то .

13. Производная тригонометрических и обратных тригонометрических функций.

14. Неявная функция и ее производная.

Пусть неявная функция y от х определяется равенством:

(1)

Дифференцируем по х все члены этого равенства помня, что y есть функция от х:

Отсюда находим: (2)

Равенство (2) снова дифференцируем по х (имея в виду, что y есть функция от х):

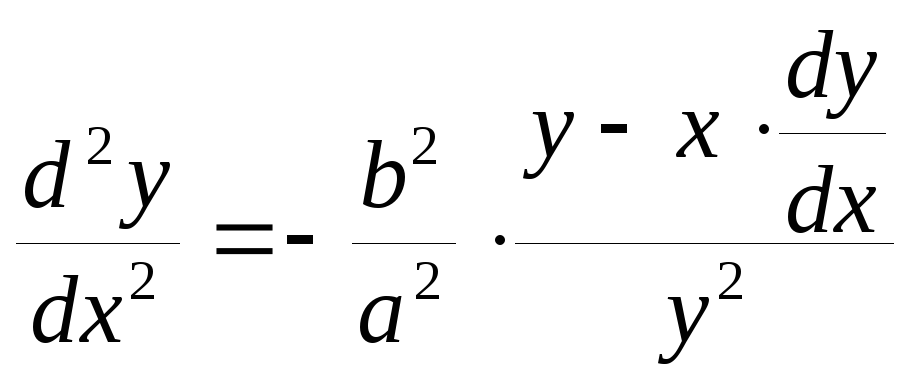
Подставляем вместо производной ее выражение из равенства (2), получаем:

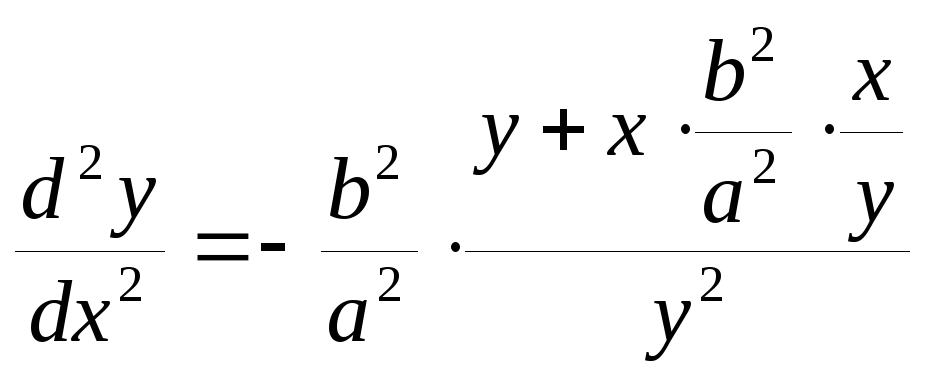
или после упрощения

из уравнения (1) следует, что поэтому вторую производную можно представить в виде

Дифференцируя это равенство по х найдем и т.д.