2. Предел функции. Определение, основные свойства и действия над ними.

Определение. Число – называется пределом функции при ( - число), то есть если для любого существует такая окрестность точки , что выполняется ; зависит от , что при .

Число является пределом функции при тогда и только тогда, когда для любого существует такая окрестность точки , что выполнимо условие . Коротко этот факт записывают так: Или при .

Теорема. Для того, чтобы число было пределом функции при стремящемся к , необходимо и достаточно, чтобы каждому числу соответствовала такая окрестность точки , что значения функции для всех чисел окрестности (за исключением, быть может, самой точки ) приближают с погрешностью, меньшей .

Иначе говоря, для того чтобы необходимо и достаточно, чтобы значениям достаточно мало отличающимися от соответствовали значения функции сколь угодно мало отличающиеся от .

ДЕЙСТВИЯ НАД ПРЕДЕЛАМИ.

Пусть имеется

и

Тогда:

1. 

2. 

3. Если – действительное число, то

4. При дополнительном предположении, что , получим

.

3. Первый и второй замечательный предел.

- ПЕРВЫЙ ЗАМЕЧАТЕЛЬНЫЙ ПРЕДЕЛ

- ВТОРОЙ ЗАМЕЧАТЕЛЬНЫЙ ПРЕДЕЛ

4. Односторонние пределы. Определение и их особенности.

Введем понятие левой и правой окрестности точки ( - число).

Определение. Любой интервал окрестности точки , правым концом которого является точка , называется ее левой окрестностью.

Аналогично, любой интервал, концом которого является точка , называется правой окрестностью.

Символическая запись обозначает, что принимает значения, принадлежащие некоторой левой окрестности точки , то есть .

Аналогично, запись обозначает, что .

Определение. Формула , где функция определена на множестве и –предельная точка этого множества ( - конечно), а – число, обозначает, что при любом выполняется при (предел функции слева).

Аналогично, формула ( - число) имеет следующий смысл: при , где произвольно и окрестность точки зависит от (предел функции справа).

Для чисел и употребляется символическая запись и .

Если функция определена в точке , то ее значение в этой точке обозначается через , конечно, оно может не совпадать с числами и .

Из определения предела легко следует, что если функция имеет предел, то у нее существует как левосторонний, так и правосторонний пределы и они оба равны пределу функции.

Однако из существования, например, правостороннего предела нельзя сделать никаких выводов о пределе функции или о левостороннем пределе.

5. Непрерывность функции в точке и области, основные условия.

Определение: Функция определённая на множестве Х называется непрерывной, при ( или непрерывной в точке ), если:

1. Функция определена при (т.е. )

2. Приращение функции в точке стремится к нулю, когда приращение аргумента стремится к нулю, то есть

где бесконечно малое приращение пробегает лишь те значения, для которых имеет смысл. При этом мы предполагаем, что является предельной точкой множества и таким образом, в любой окрестности найдутся точки отличные от для которых функция определена.

По-другому говоря, функция называется непрерывной в данной точке, если в этой точке бесконечно малому приращению аргумента, соответствует малое приращение функции.

Определение: Функция называется непрерывной на данном множестве Х, если

1. она определена на множестве Х;

2. непрерывна в каждой точке этого множества, то есть для всех справедливо равенство:

где

Необходимое и достаточное условие непрерывности функции.

Теорема: Для того чтобы функция определённая в окрестности точки была непрерывной в этой точке необходимо и достаточно, чтобы значениям Х достаточно мало отличающимся от соответствовали значения функции сколь угодно мало отличающиеся от , то есть другими словами говоря, чтобы для каждого числа можно было найти такую окрестность точки , что значения функции при меньше чем на .

Без доказательства.

6. Точки разрыва, их классификация.

Определение: Точка в которой нарушается непрерывность функции называется точкой разрыва этой функции.

Это означает, что в какой-то точке для функции не выполняется по крайней мере одно из условий непрерывности, то есть если при функция не определена или не существует предел

или

при произвольном стремлении хотя выражения, стоящие и справа и слева существуют, то при функция разрывна, а точка есть точка разрыва.

Определение: Если функция такова, что существую конечные пределы.

и ,

но или или значение функции при не определено, то называется точкой разрыва 1-ого рода. Все остальные точки разрыва называются её точками разрыва 2-ого рода.

7. Элементарные функции, их непрерывность.

1. Степенная функция ,где n-натуральное число, непрерывна при любом значении .

2. Показательная функция при непрерывна при любом значении

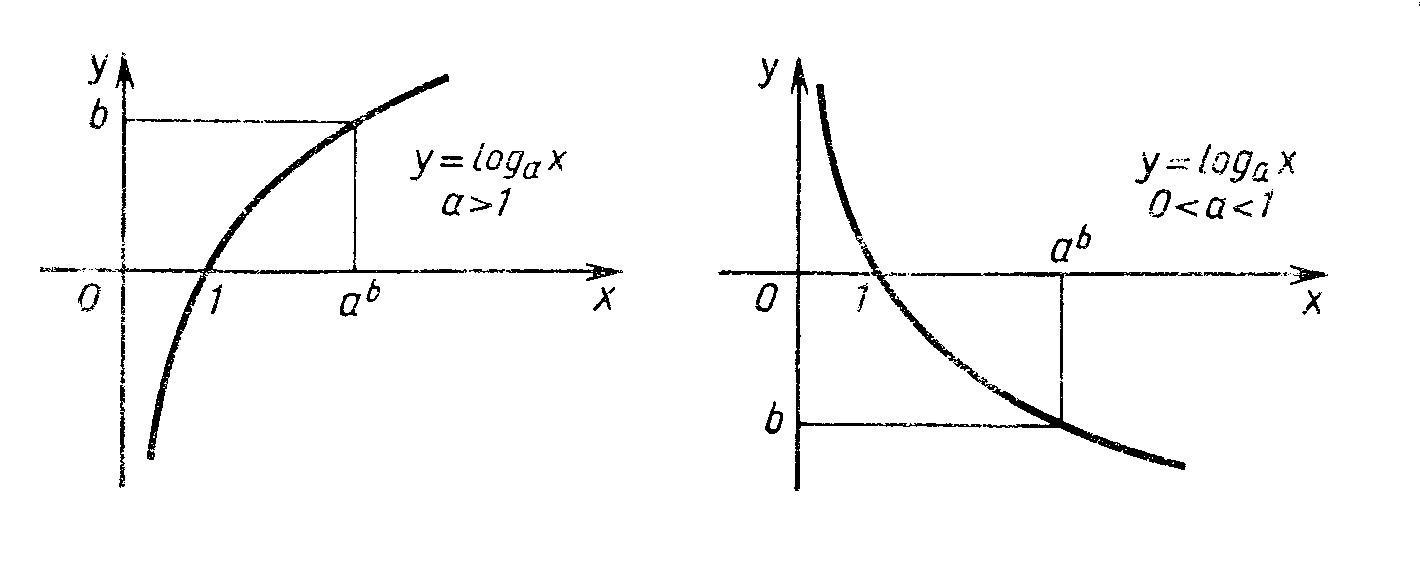
3. Логарифмическая функция при a>0; a1 определена только при . Так как обратная функция строго монотонна и непрерывна, то и непрерывна для всех положительных значений .

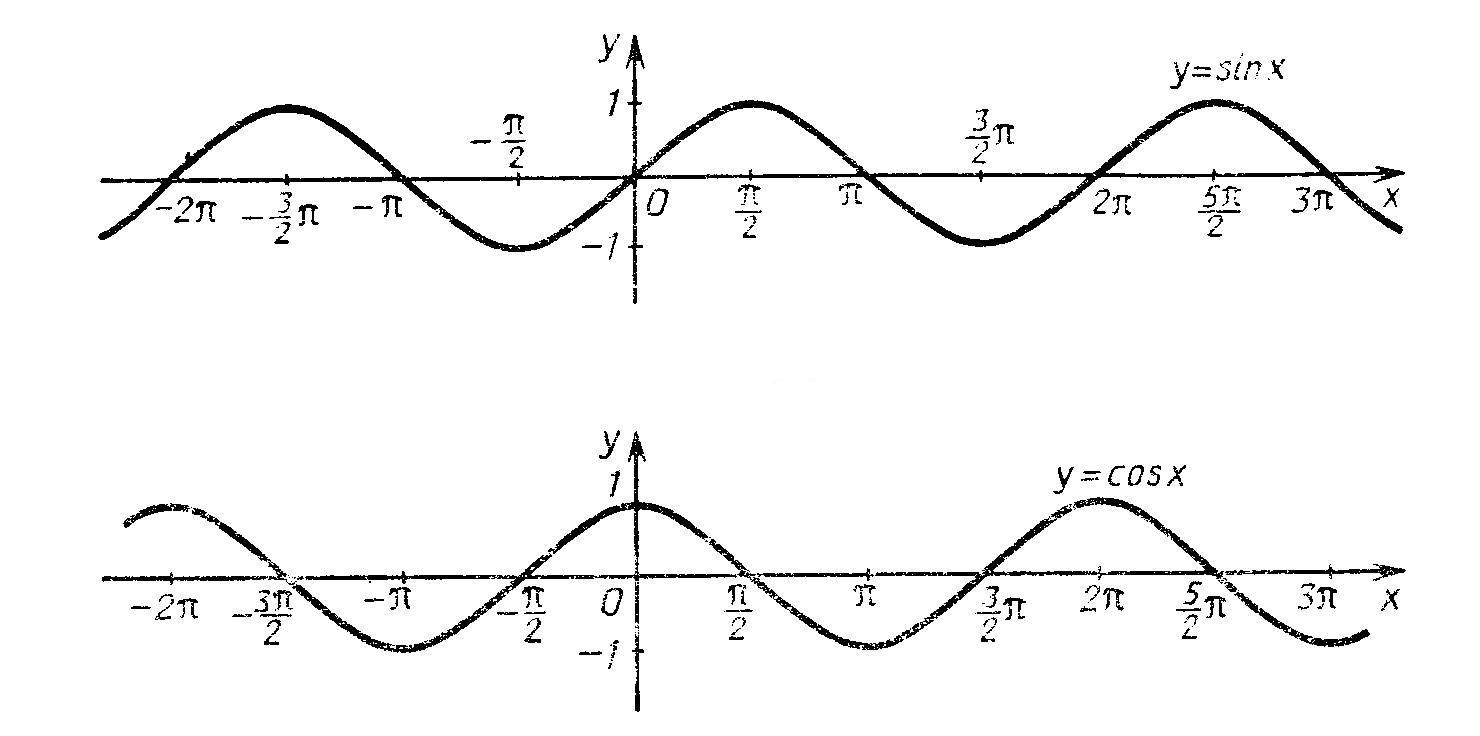
4. тригонометрическая функция ; непрерывны для всех значений .

- эта функция определена и непрерывна для всех значений , для которых .

Исключительными являются значения

- эта функция определена и непрерывна для всех значений, для которых .

Исключительными являются значения вообще где .

8. Производная функции. Определение.

Дадим определение производной:

«Производной данной функции по аргументу называется предел отношения приращения аргумента функции к приращению аргумента , когда последнее произвольным образом стремится к нулю».

или .

Операция нахождения производной от функции называется дифференцированием функции.

Определение: Если функция имеет производную в точке , то есть если существует

,

Определение: Если функция дифференцируема в каждой точке некоторого отрезка или интервала , то говорят, что она дифференцируема на отрезке или, соответственно, в интервале .

Теорема: Если функция дифференцируема в некоторой точке , то она в этой точке непрерывна. Таким образом, в точках разрыва функция не может иметь производной.