3. Функции нескольких переменных.

Частной производной функции по переменнойв точкеназывается предел

.

Аналогично определяются частные производные по и по. При дифференцировании по одной переменной все остальные считаются постоянными.

Например, если , то

, ,.

Градиентом функции называется вектор

Производной функции по направлению вектора, где, называется число

.

Теорема о полном дифференциале гласит, что

.

Поэтому

.

Если , то для взятия производной по направлению нужно предварительно нормировать вектор , поделив его на длину .

Касательная к кривой, заданной неявным уравнением , в точкеопределяется уравнением

**.

Нормаль к той же кривой определяется уравнением

.

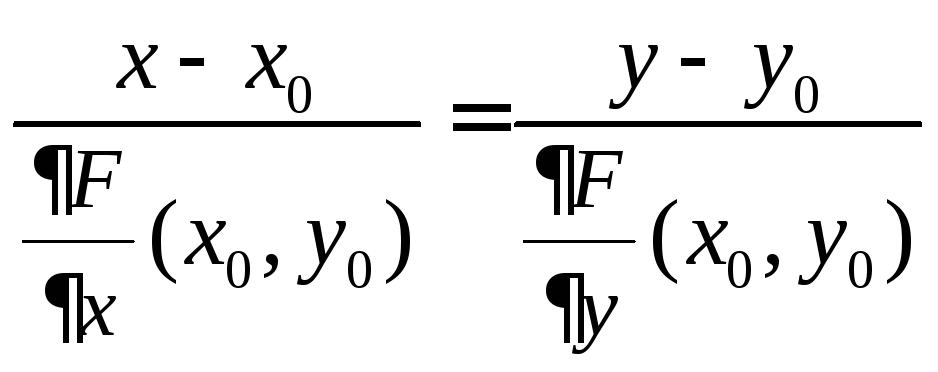Задача 3.1.Найти градиент функциив точке (1,5).

Решение. Имеем:

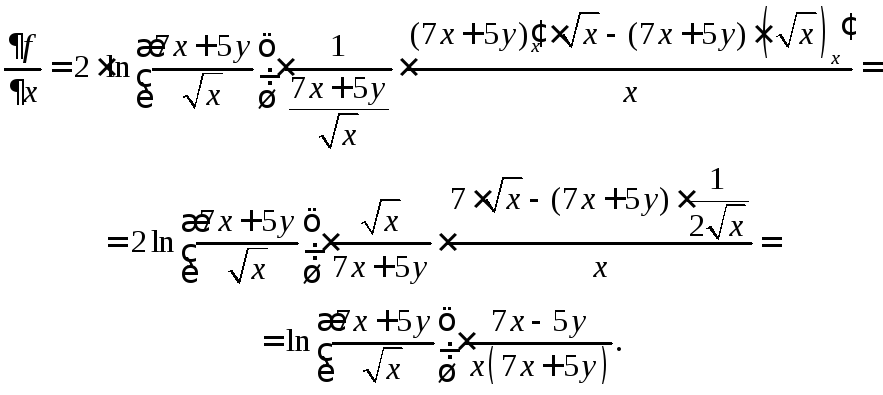Подставляя 1 вместо и 5 вместо, получим

.

Аналогично,

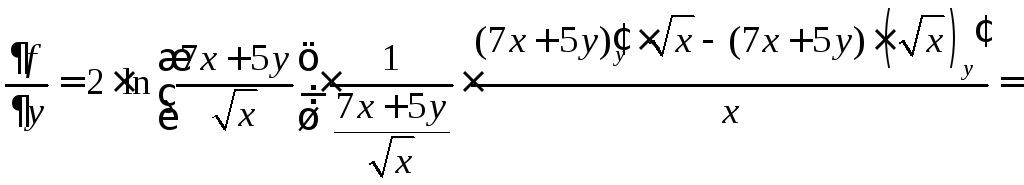
откуда . Окончательно,

.

Задача 3.2. Вычислить производную функции по направлению векторав точке (1,1).

Решение. Длина вектора равна , поэтому перейдем к вектору , имеющему то же направление, что и вектор, но единичную длину. Далее,

, .

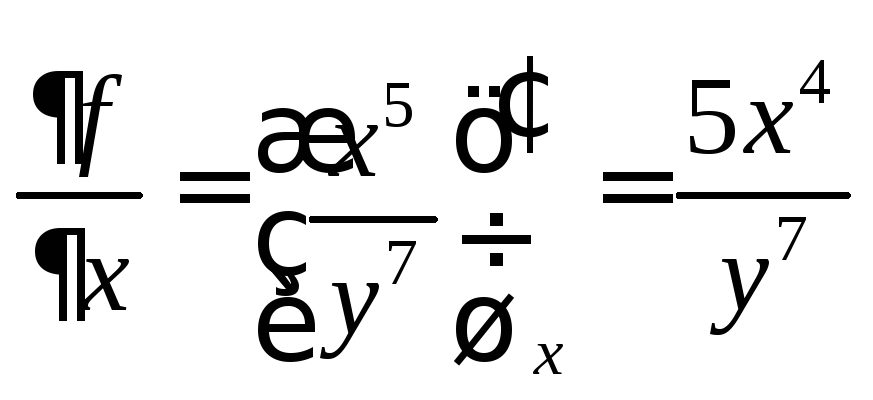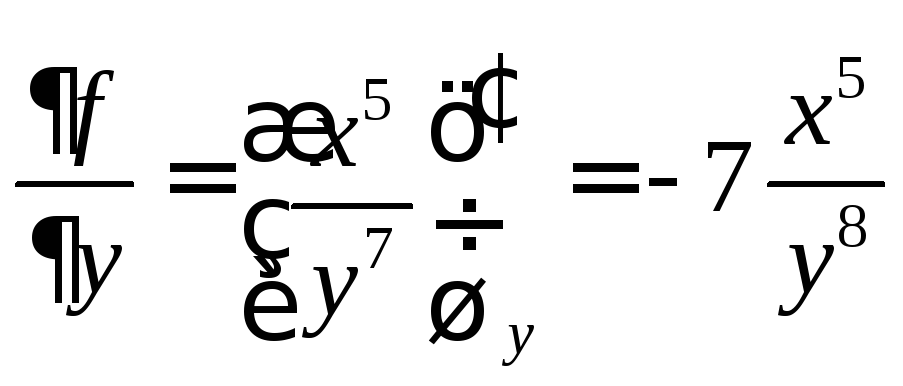В точке имеем . По определению производной по направлению получаем:

.

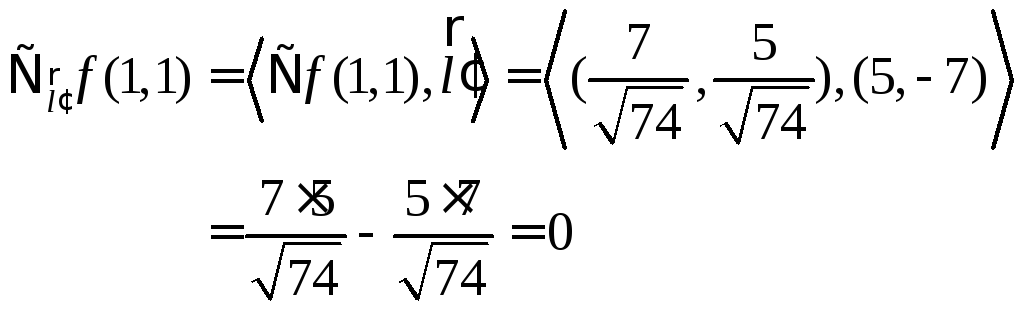Задача 3.3. Найти производные функции.

Решение. Имеем:

,

.

По определению вторых частных производных, имеем:

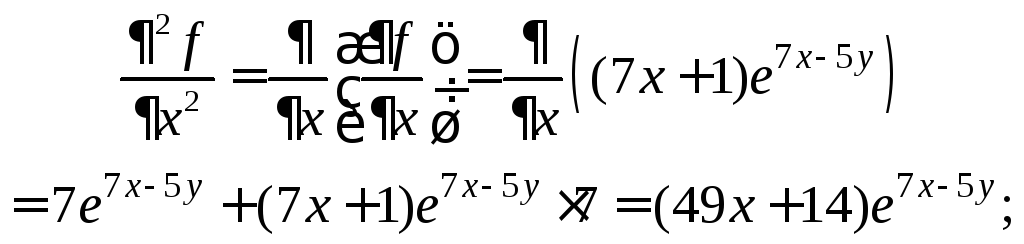
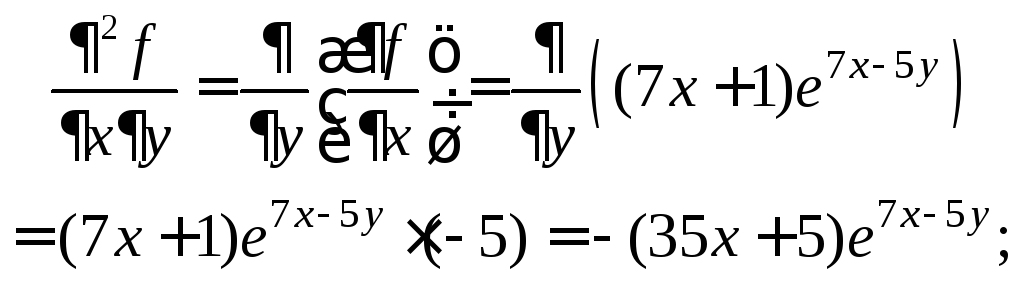
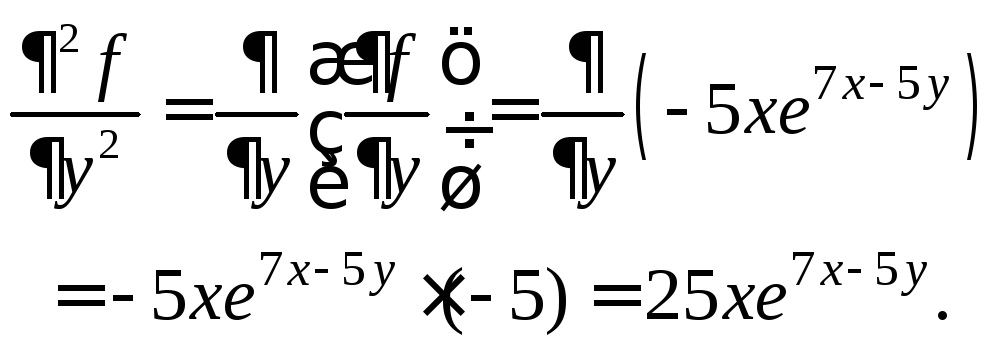
Задача 3.4. Для кривой, задаваемой уравнением , написать уравнения касательной и нормали в точке (1,1).

Решение.Подставим в уравнение касательной и нормали значения частных производных функциив точке.

, .

Уравнение касательной имеет вид:

.

Уравнение нормали имеет вид

.

4. Интегральное исчисление. Неопределенные интегралы.

Операция интегрированияявляется обратной к операции дифференцирования.

Определение 1.Функцияназывается первообразной для функции, если.

У функции имеется бесконечное множество первообразных, при этом все они отличаются друг от друга на константу: еслии- две первообразные для функции, то, гдеС=const.

Определение 2.Множество всех первообразных для функцииназывается неопределенным интегралом оти обозначается символом.

Если любая первообразная для, то, гдеС =const.

Основные свойства неопределенного интеграла.

1. (в частности,).

2. .

3. .

Необходимо знать интегралы основных элементарных функций (табличные интегралы):

()

Для нахождения интегралов используются следующие методы.

1) Преобразование подынтегрального выражения, при помощи которого интеграл преобразуется к одному или нескольким табличным интегралам.

2) Подведение под знак дифференциала, основанное на формуле .

,

где .

3) Замена переменной. Если , то

.

4) Интегрирование по частям:

.

5) Интегрирование рациональных дробей вида (где,многочлены) основано на представлении дробив виде суммы многочленаи простейших рациональных дробей вида

.

Разложение рациональных дробей в сумму простых дробей осуществляется с помощью метода неопределенных коэффициентов, который будет продемонстрирован ниже, на частном примере.

Имеют место формулы

,

().

Интеграл можно найти, выделяя полный квадрат в знаменателе:, с последующей заменой.

Интеграл сводится к интегралу следующего вида:

.

6) Функции, содержащие иррациональности, интегрируются в том случае, когда интеграл от них сводится к интегралу от рациональной дроби с помощью какойлибо замены переменной. Приведем несколько примеров интегрируемых иррациональных функций.

) Интегралы вида

где  рациональная функция, а , ,  натуральные числа. Метод интегрирования  замена , где  наименьшее общее кратное чисел , , .

) Интегралы вида сводятся к табличным при помощи замены .

) Интегралы , где , и  рациональные числа. Интегралы такого вида сводятся к элементарным только при следующих соотношениях параметров , и .

Если целое, то следует использовать замену , где  наименьшее общее кратное знаменателей дробей ,.

Пусть теперь  наименьшее общее кратное знаменателей дробей ,. Если  целое, то интеграл сводится к интегралу от рациональной функции с помощью замены .

Если целое, то интегрирование осуществляется при помощи замены .

) Подстановки Эйлера. Они применяются к интегралам вида , гдерациональная функция. Имеется три вида подстановок Эйлера.

;

;

,

где , корни многочлена .

Тригонометрические замены. Для интегралов используется замена.Для интегралов используется замена. Для интегралов используется замена. В каждом из трех случаев получается интеграл от рациональной функции, зависящей оти.

7) Интегрирование выражений вида , где– рациональная функция от . В разных случаях используются замены ,, , . Если ни одна из этих замен не позволяет получить интеграл от рациональной функции, то используется универсальная тригонометрическая подстановка. Тогда,,,и подынтегральное выражение сведется к рациональной дроби.

В задачах 4.1.а4.1.ж.требуется вычислить неопределенные интегралы.

Задача 4.1.а. .

Решение. .

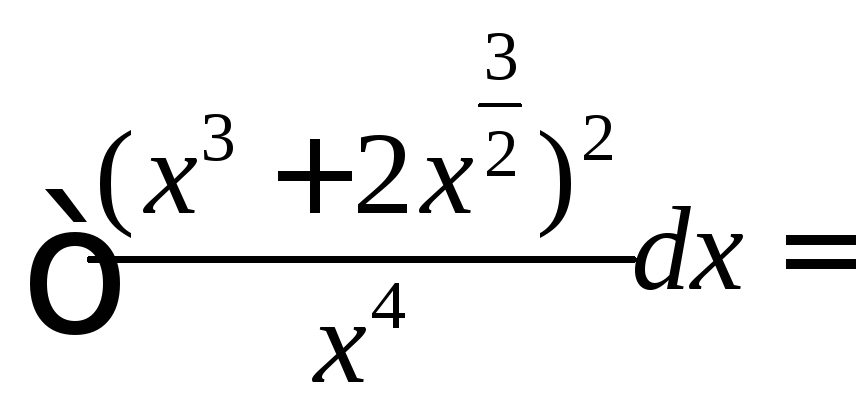
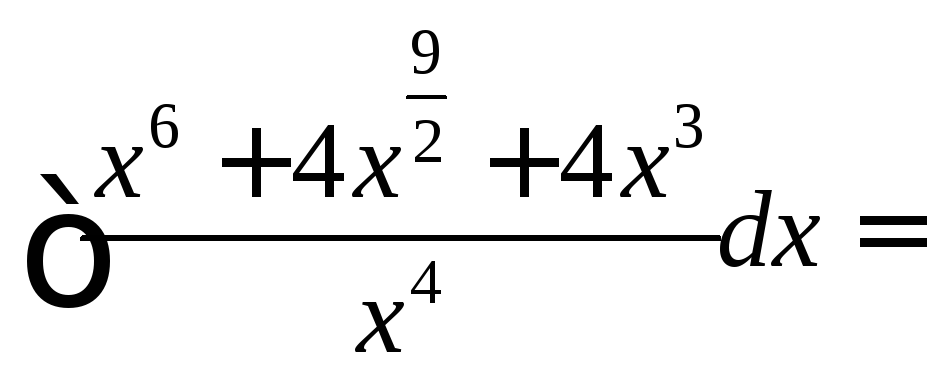
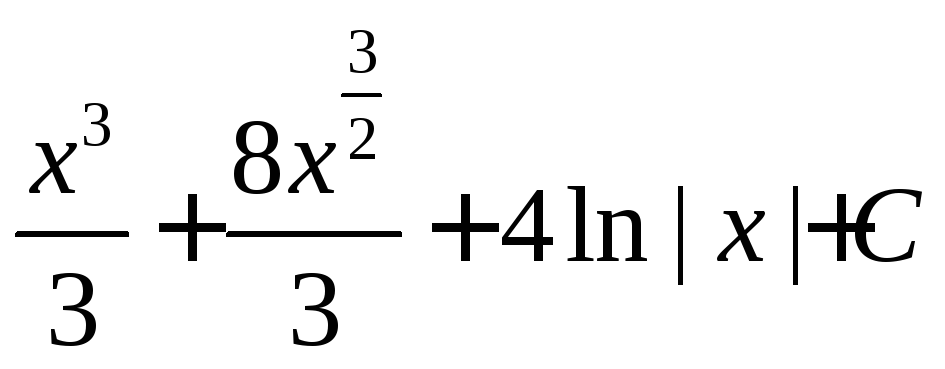Задача 4.1.б..

Решение.

1)

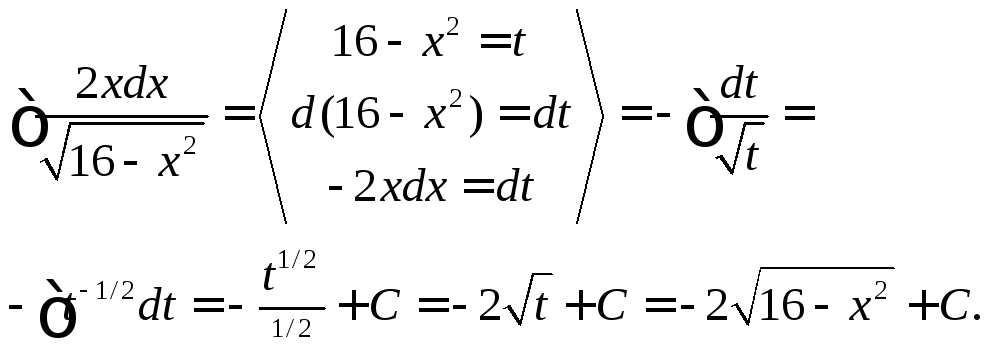
2) .

Ответ:.

Задача 4.1.в..

Решение.=========.

Задача 4.1.г..

Решение.Интегрируем по частям: =.

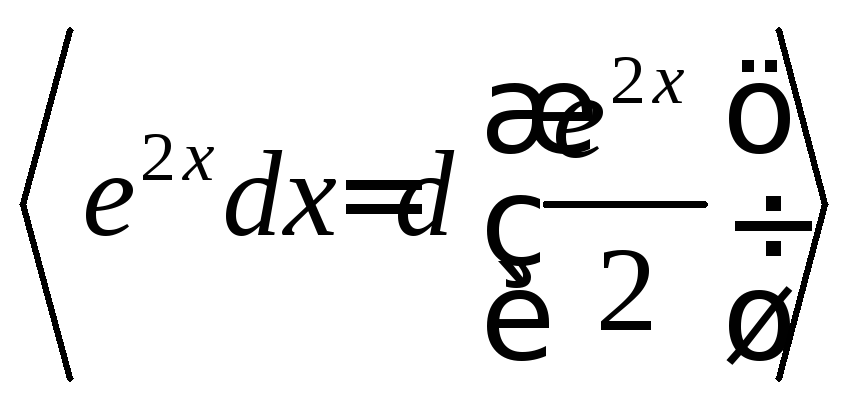
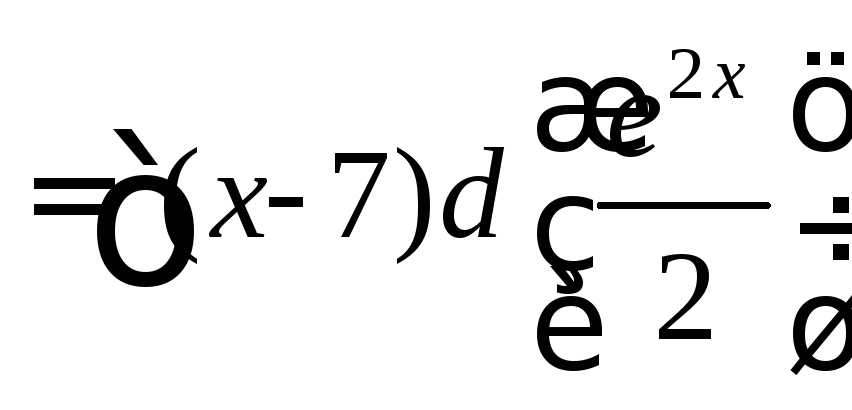
Интегралы вида находятся с помощью подстановки.

Задача 4.1.д..

Решение. =======.

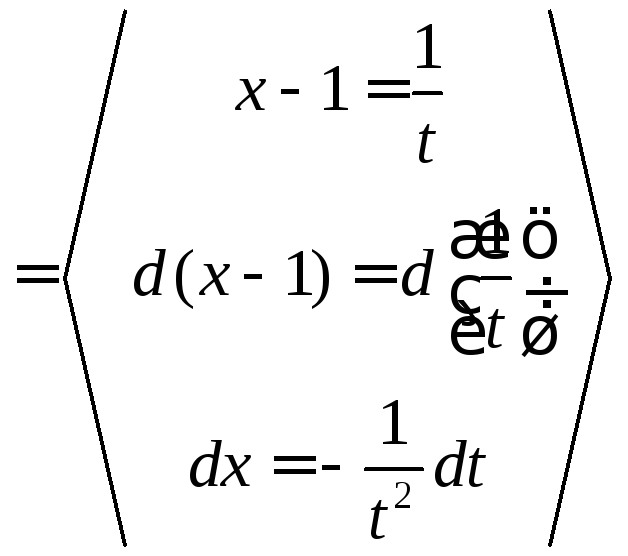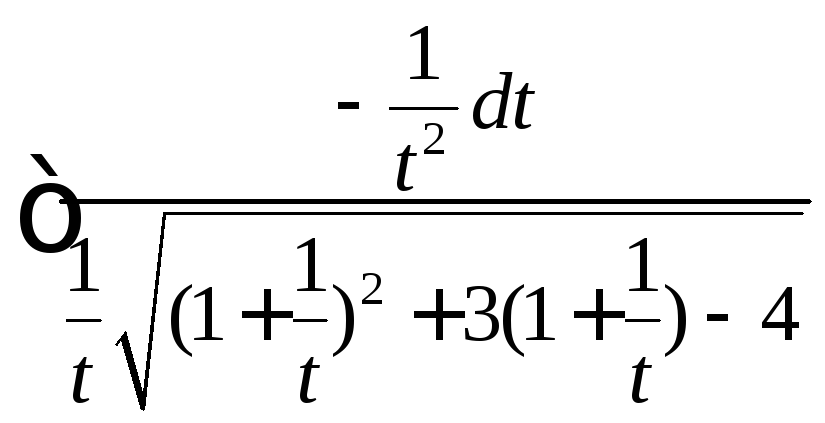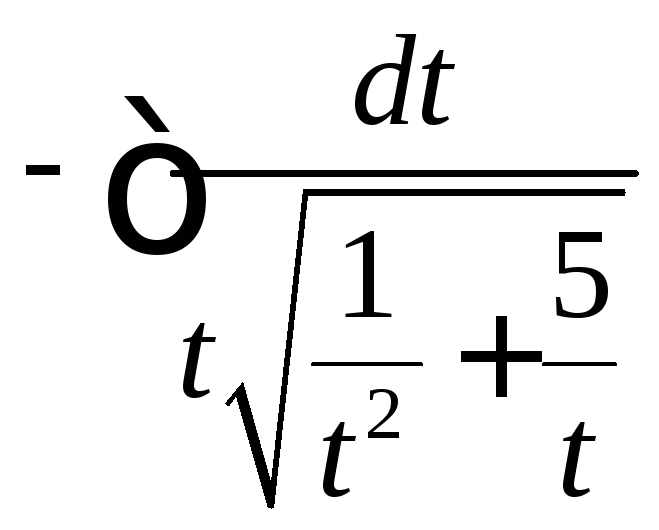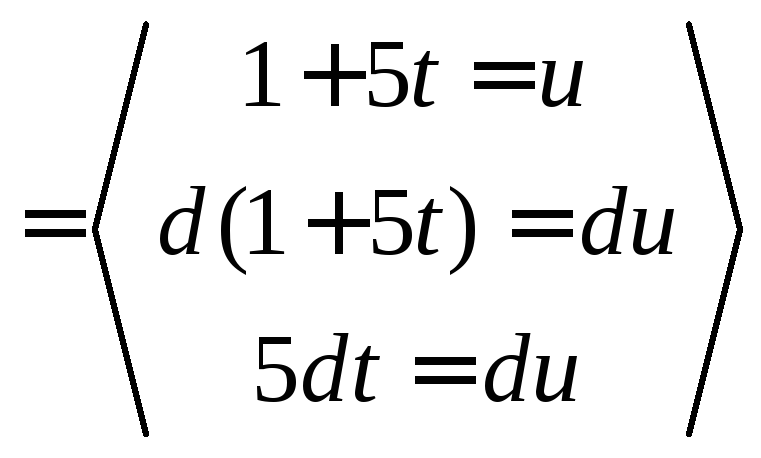Задача 4.1.е..

Решение.Разложим подынтегральную функцию в сумму простых дробей. Воспользуемся методом неопределенных коэффициентов.

,

,

,

откуда



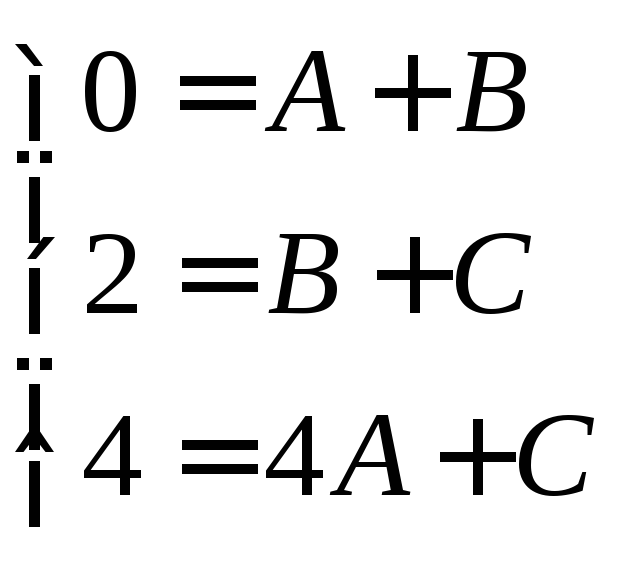
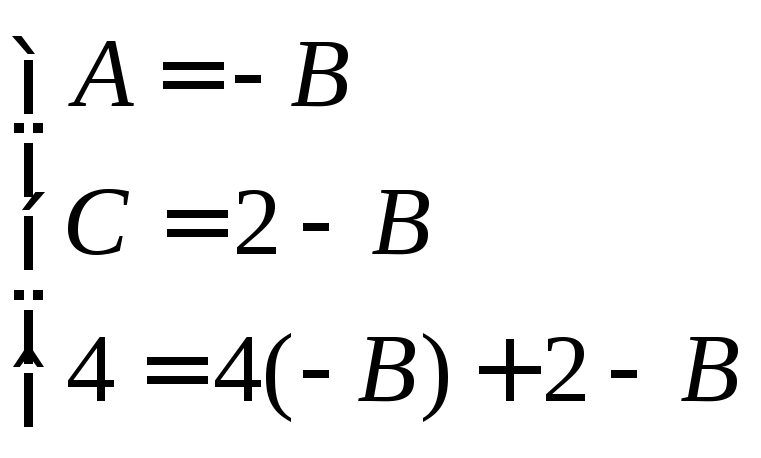
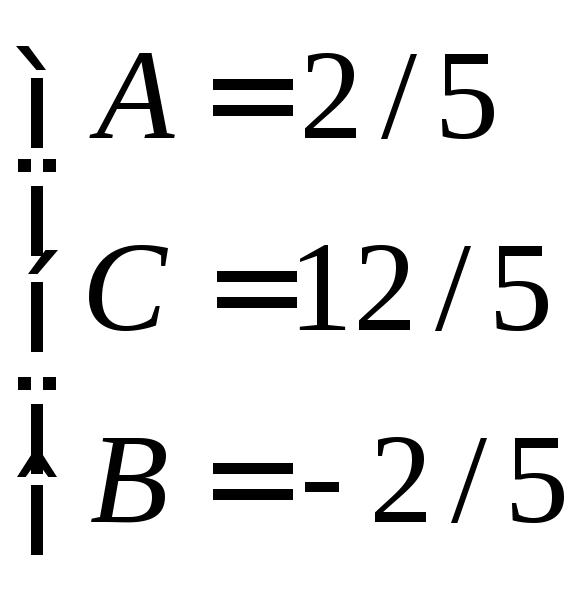
Следовательно,

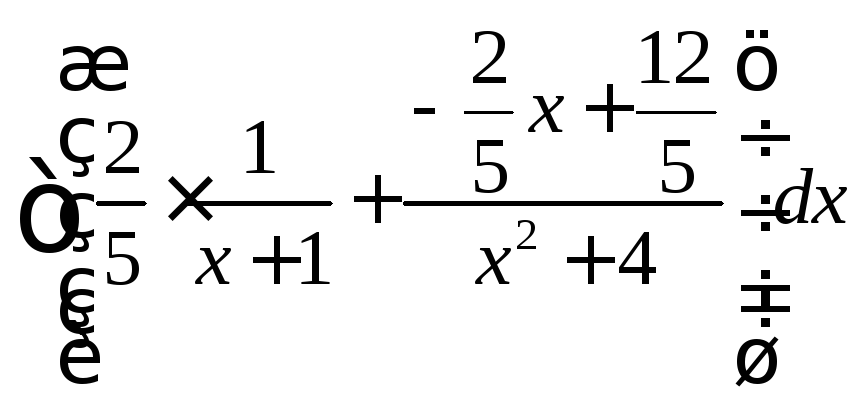
1) ;

2)

=.

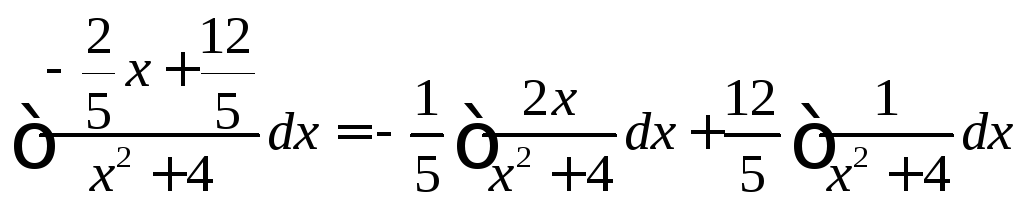
Ответ: .

Интегралы вида для нечетногоможно находить при помощи подстановки.

Задача 4.1.е..

Решение. .

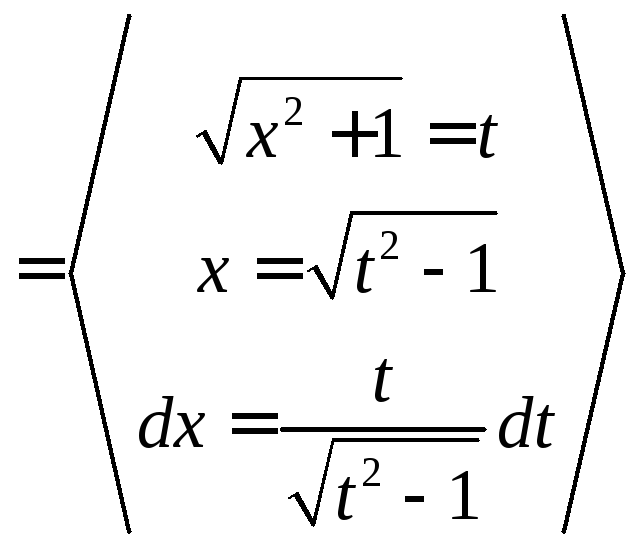
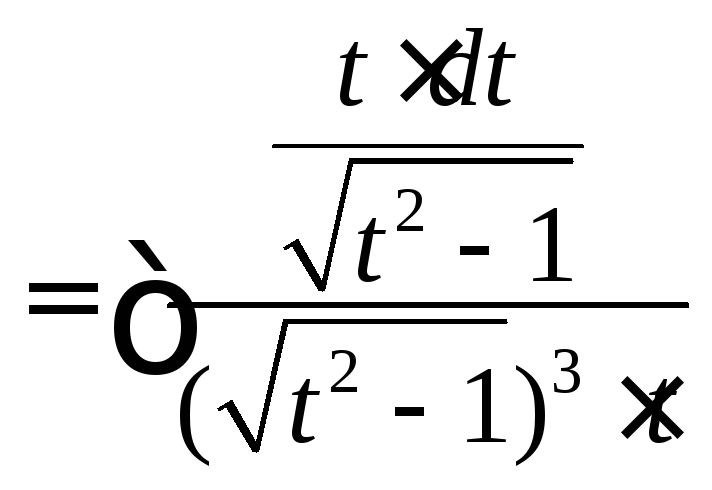
Разложим подынтегральное выражение в сумму простых дробей:

,

,

Приравнивая коэффициенты при одинаковых степенях в левой и правой частях тождества, получим систему четырех уравнений с четырьмя неизвестными A,B,C,D:



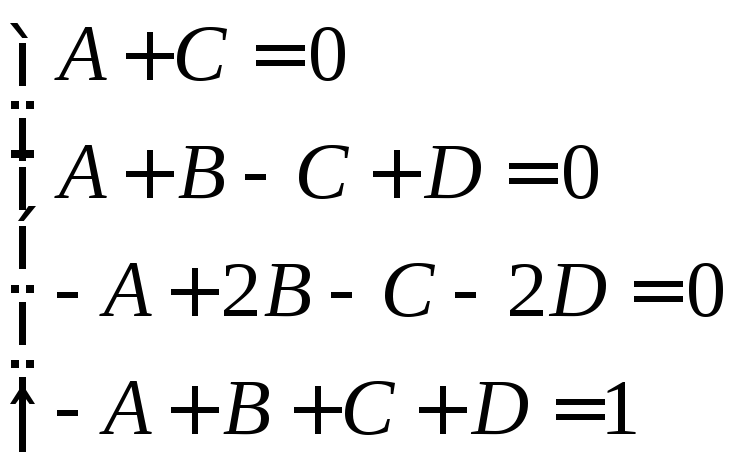
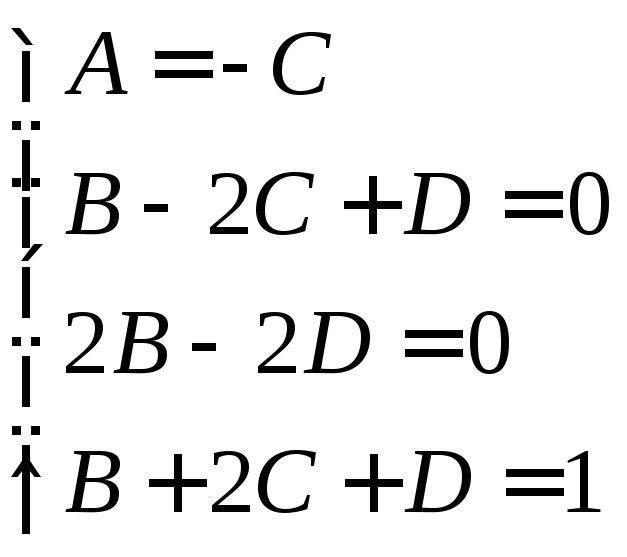
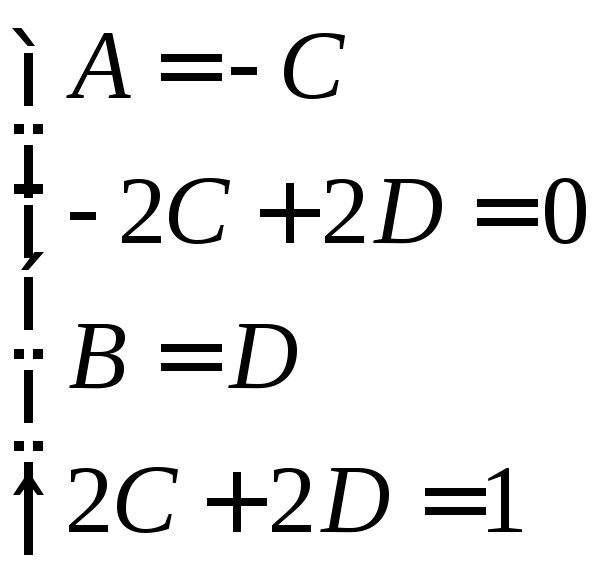
откуда

Окончательно, получим . Следовательно, разложение дроби в сумму простейших имеет вид:

.

В результате, получаем

===.

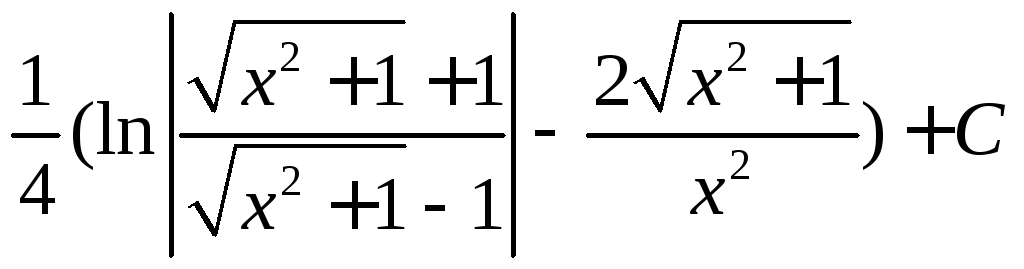Задача 4.1.ж. .

Решение.Используем универсальную тригонометрическую подстановку.

=====.

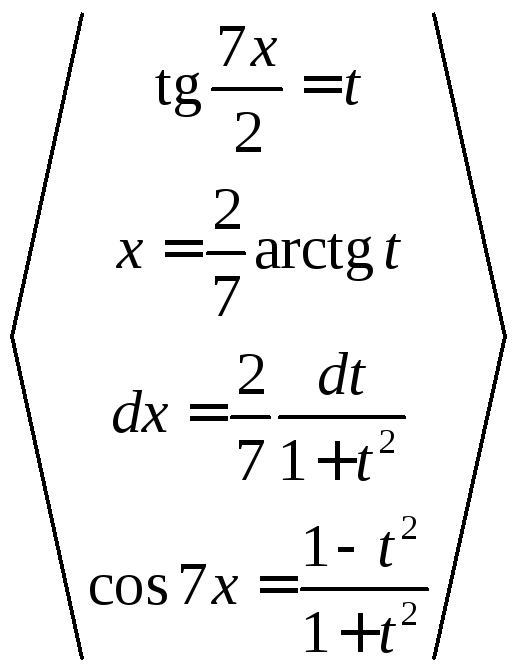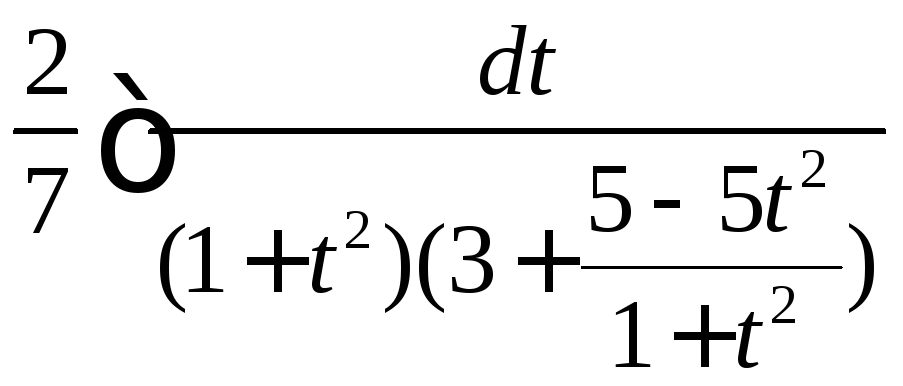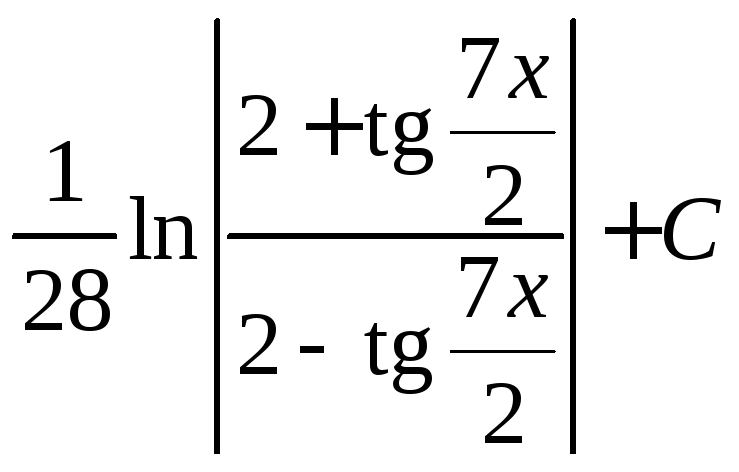Определенные интегралы. Площади плоских фигур.

Определенный интеграл (Римана) позволяет распространить формулу площади прямоугольника на площадь более или менее произвольной плоской геометрической фигуры. В основе понятия определенного интеграла лежит так называемая интегральная сумма, определяемая следующим образом. Пусть задана функция , определенная на отрезке. Разобъем отрезокпроизвольным образом начастей,,(,). В частности, можно разбитьнаравных частей, тогда длина каждого отрезка разбиения будет равна. В общем случае, пусть

.

Возьмем, опять же произвольным образом, внутри каждого из отрезков по точке.Интегральной суммой функции напо разбиениюназывается число

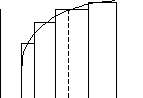
Если , то интегральная сумма есть площадь фигуры, состоящей из прямоугольников со сторонамии , . Интуитивно ясно, что, чем меньше максимальная длина отрезков разбиения, тем точнее эта фигура из прямоугольников приближает криволинейную трапецию с основаниями,и “боковыми сторонами”,. Интеграл от функциипо отрезку есть предел по всевозможным разбиениям , когда .

Предел понимается здесь в обычном смысле: число называетсяопределенным интегралом от по (обозначается как ), если для произвольногонайдется такое , что, как только разбиение отрезка удовлетворяет условию , интегральная сумма, отвечающая этому разбиению, будет отличаться отне больше, чем на : .

Геометрический смысл определенного интеграла.

Значение (с точностью до знака) есть площадь криволинейной трапеции, заключенной между графиком функции , осью абсцисс и прямыми ,. В частности, если на отрезке заданы две функции и, причем, то площадь криволинейной трапеции, заключенной между графиками этих двух функций, равна.

Связь между определенным и неопределенным интегралом заключена в формуле НьютонаЛейбница:

,

или, в другой записи, , где произвольная первообразная функции .

Справедливы следующие две формулы – замена переменной интегрирования и интегрирование по частям.

Замена переменной.

Пусть  произвольная непрерывно дифференцируемая функция, определенная на некотором отрезке , причем,, ипри любом. Тогда

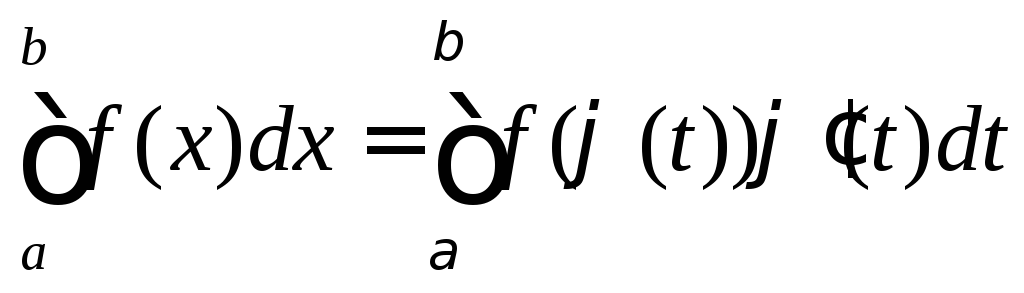
Интегрирование по частям.

.

Задача 4.2.а.Найти площадь фигуры, ограниченной линиями,.

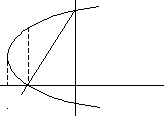
Решение.Заметим, что первое уравнение является уравнением параболы, ветви которой направлены вправо. Второе уравнение определяет прямую линию.

Найдем пересечения графиков функций и сделаем рисунок. Для этого решим систему



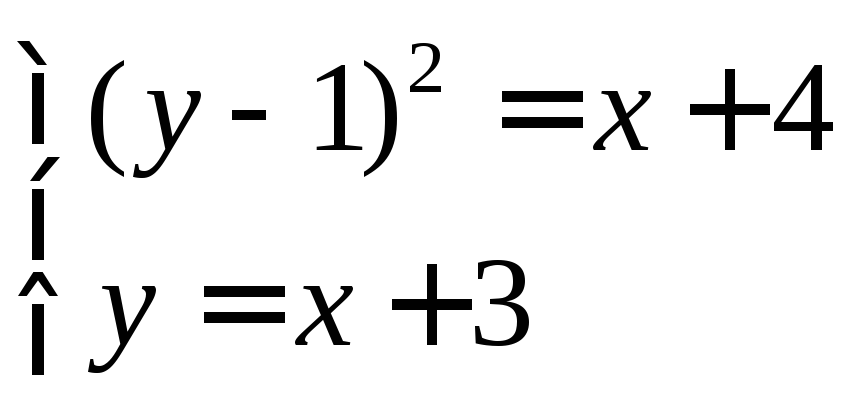
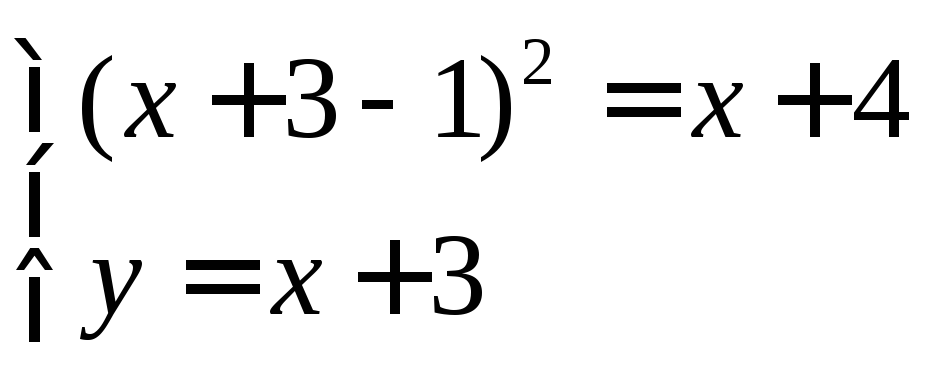
откуда , что дает и .

3

0

Из рисунка видно, что фигура состоит из двух частей. При получаем сегмент параболы. Прикриволинейная трапеция заключена между прямой и параболой. Следовательно, площадь фигуры равна сумме двух следующих двух интегралов:

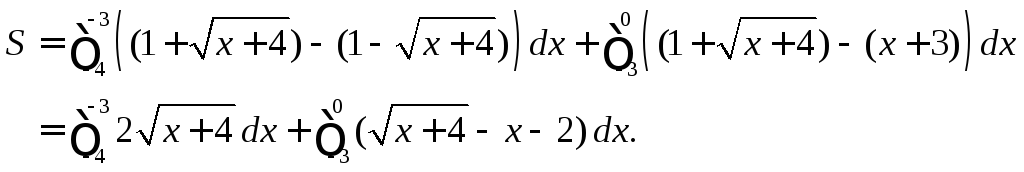Для первого интеграла получаем:

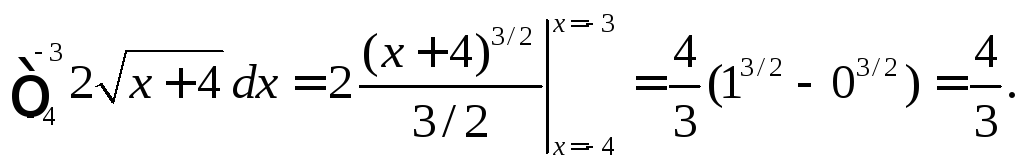
Для второго интеграла получаем:

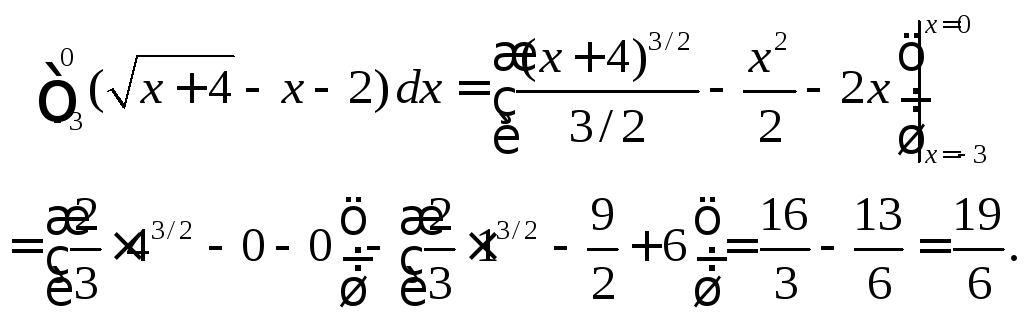
Таким образом, .Ответ: .

Задача 4.2.б.Найти площадь фигуры, ограниченной линиями, ,.

Решение.На отрезкевыполняется неравенство. Поэтому найдем площадь, используя формулу.

=.
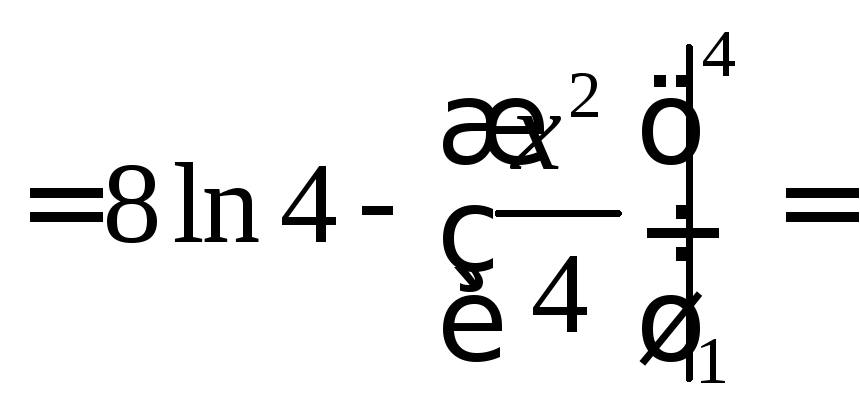