
шпоргалка / angem
.doc
ЛИНЕЙН. ОПЕРАЦ. НАД ВЕКТОР.
Вектор характеризуется числовым значением и направлением. Модуль вектора АВ – длина отрезка АВ. Прим. В геометрии векторы считаются свободными, т.е. допустим их свободный перенос в пространстве без изменения направления. Нулевой вектор (), вектор у которого начало и конец совпадают. Противоположный вектор – вектор той же длины, но обратного направления.
Опр.: два вектора называются коллинеарными, если они лежат на параллельных прямых. Опр.: три вектора называются компланарными, если они лежат в параллельных плоскостях. Суммой двух векторов a и b, будет вектор с, начало которого совпадает с началом а, а конец с концом b, при условии, что начало b совпадает с концом а. Произведение вектора а на число Р, называется вектор Ра: |Ра|=|P|*|а|, Ра||a. Разность векторов а и b, будет с: с+b=а => c=a-b (или c=a+(-b)). Орт вектора – единичный вектор e=a / |a|. Св-ва лин. операц. a+b=b+a, a+(b+c)=(a+b) +c, a+нул.вект.=a, a+(-a)=нул.вект., 1a=a, p(ka)=pka, p(a+b)=pa+pb, (p+k) a=pa+ka.
ЛИНЕЙН. ЗАВИСИМ. ВЕКТОРОВ.
Пусть задана система векторов а1, а2, а3,…,ал (1) одной размерности.
Опр.: система векторов (1) называется линейно-независимой (ЛН), если равенство 1а1+2а2+…+лал=0 (2) выполняется лишь в том случае, когда все числа 1, 2,…, л=0. Опр.: система векторов (1) называется линейно-зависимой (ЛЗ), если равенство (2) выполнимо хотя бы при одном i≠0 (i=1,…,k). Св-ва: 1.Если система векторов содержит нулевой вектор, то она линейно зависима. 2. Если система векторов содержит линейно-зависимую подсистему векторов, то она будет линейно-зависимой. 3. Если система векторов ЛН, то и любая ее подсистема будет линейно независимой. 4.Если система векторов содержит хотя бы один вектор, являющийся линейной комбинацией других векторов, то эта система векторов будет линейно зависимой.
ПОНЯТИЕ ЛИН. ПРОСТР.. БАЗИС.
Линейное векторное пространство – множество для элементов которого определены операции сложения и умножения на число. Опр.: пусть задана некоторое ЛВП. Базисом называется совокупность линейно-независимых векторов системы с помощью которых можно выразить любой другой вектор ЛВП. Теорема: В n-мерном пространстве любые n ЛЗ векторов образуют базис. Теорема: Разложение вектора по базису единственно. Док-во: В (е1, е2, …, еп), ! 1, 2, п: а=1 е1 + 2 е2 +…+ п еп. Док-во от противного, пусть а – имеет еще одно разложение, перемножим вектора, получим ЛЗ систему, а значит разложения совпали.
Опр.: Коэфф. Разложения вектора по данному базису – есть координаты вектора в данном базисе. Услов. колл. a||b, a=pb=> x1/x2=…z1/z1=p.
СКАЛЯРНОЕ ПРОИЗВ. ВЕКТОР.
Опр.: скалярным произведением двух векторов называется произведение длин двух векторов на косинус угла между ними.
( а,b)=|a|
|b| cos ,
<90,
пр-е полож.; =90,
пр-е =0; >90,
пр-е отриц.
а,b)=|a|
|b| cos ,
<90,
пр-е полож.; =90,
пр-е =0; >90,
пр-е отриц.
Свойства: 1. (а,b)= (b,а) 2. (aа,b)= a (а,b) 3. (а+b,с)= (а,с)+ (b,с) 4. (а,а)=|a|2 – скал.квадрат. Опр.: два вектора называются ортогональными, когда скалярное пр-е равно 0. Опр.: вектор называется нормированным, если его скал.кв.равен 1.
cos=a,b/|a||b|=x1x2+y1y2+z1z2/sqrt(x12+y12+z12)*sqrt(x22+y22+z22)
Работа – A=(F,S).
ВЕКТОР. ПРОИЗВ. ВЕКТОРОВ.
Опр.: векторным произведением двух векторов a и b обозначаемым [a,b] называется вектор с удовлетворяющий след. требованиям: 1. |c|=|a||b|sin j. 2. (с,а)=0 и (с,b)=0. 3. а, b, с образуют правую тройку.
Св-ва: 1. [a,b]= - [b,a] 2. [aа,b]= a [а,b] 3.[a+b,c]=[a,c]+[b,c] 4. [a,a]=0
Теорема: Длина векторного произведения векторов равна площади параллелограмма построенного на этих векторах. Док-во: справедливость теоремы вытекает из первого требования определения векторного произведения. Теорема: Пусть векторы а и b заданы координатами в ортонормированном базисе, тогда векторное произведение равно определителю третьего порядка в первой строке которого находятся базисные векторы, во второй – координаты первого вектора, в третьей – координаты второго.
Момент силы – [a,b], к точке а относительно b.
ОПРЕДЕЛИТЕЛИ
Опр.: Число a11a22-a12a21 называется определителем квадратной матрицы (2). Числа аij-элементы определителя. Определителем кв. матрицы (3) называется число равное: а11а22а33+а21а32а13+а12а23а31-а31а22а13-а32а23а11-а21а12а33. (схема треуг.).
Порядком О называется размерность матрицы для которой найден определитель. Св-ва: 1. величина О не изменится если его транспонировать. 2. Знак О изменится если поменять местами два паралл. ряда. 3. О с двумя одинаковыми рядами равен нулю. 4. О с нулевым рядом равен нулю. 5. Общий множитель элементов какого-либо ряда можно вынести за знак О. 6. Из св. 3 и 5 – О с пропорциональными рядами равен нулю. 7. Если элементы ряда представляют собой суммы, то О может быть разложен на несколько О (по кол-ву слагаемых). 8. Из св. 5,4,3 - О не изменится если к элементам ряда прибавить соответ. элементы паралл. ряда умн. на любое число (0). Опр: Мij – минор элемента ij – число равное О, полученному путем вычеркивания рядов на пересечении которых находится элемент. Аij – алг. дополн. элем. ij – (-1)I+J Mij.
Опр: О равен сумме произв. элементов некоторого ряда на соотв. им алгеб. доп.
МЕТОД КРАМЕРА (РЕШ. СЛАУ)
Основные понятия: Основная матрица составлена из коэфф. системы, замещая каждый столбец на свободные члены СЛАУ получаем доп. матрицы. Xn=n/(где n-номер замещаемого столбца, -определ.)
СМЕШАННОЕ ПРОИЗВЕДЕНИЕ
Опр: Смешанным произв. Трех верторов наз. (a,b,c)=(def)=a[b,c]. Св-ва: 1. (a,b,c)=(определитель 3-го порядка со строками – координатами векторов). Док-во:
2. (1a1+2a2,b,c)= 1(опред. a11, a12, a13. b1, b2, b3. c1,c2,c3.)+2(опред. a21,a22,a23,…).
3. При перестановке любых двух сомножителей, смеш. произв. меняет знак. (из 1 и св-ва опр. менять знак при перест. рядов.). Следствие: При циклической перестановке знак не меняется (a-b-c-a). 4. |(a,b,c)|=Vпарал. построенного на этих векторах, прив. к общ началу. Док-во: |(a,b,c)|=|a[b,c]|=|a||[b,c]|= |a||b||c|sin<bc=|b||c|пр.bca=SH=V.
(если тройка векторов – левая то V берется с -, иначе с + (правая если после прив. к общ нач. поворот от а к б кажется с поз. С соверш прот. час. стрел.)).
ПЛОСКОСТЬ В ПРОСТРАНСТВЕ
1. Урав. через точку _|_ вектору:
Пусть М0(x0,y0,z0), N(a,b,c) – нормальный вектор плоск. (нормаль). M0M Î P, M0M_|_N (M0M,N)=0.
=> A(x-x0)+B(y-y0)+C(z-z0)=0.
2.Общее уравнение: (из 1)
(все члены с 0 – D) => Ax+By+Cz+D=0. Опр: уравнение 1-ой степени относительно x,y,z однозначно определяет плоскость в пространстве. Док-во: коэфф. АВС не равны 0 одноврем., т.к. получ. D0. Пусть А0. A(x+D/A)+By+Cz=0. N=(A,B,C), M0 =(-D/A, 0,0)=> получ. (1 уравн.). Ч.Т.Д. (расмотреть частные случаи)
2. Урав. плоск. в отрезках: Ax+By+ Cz+D=0 (D0), x/-(D/A)+y/-(D/B)+z/-(D/C)=1 => x/a+y/b+z/c=1.
3 .
Урав. плоск. через 3 точки:
M1,M2,M3 и M
(x,y,z) ÎP.
M1M,M1M2,M1M3–компланарны
.
Урав. плоск. через 3 точки:
M1,M2,M3 и M
(x,y,z) ÎP.
M1M,M1M2,M1M3–компланарны

6. Урав. плоск. в нормал. виде.:
N0=(cosa,cosb,cosj), N0||N, p=|OM| (M-произв.), OM= пр.N0OM=(OM*N0)/|N0|=(xcosa+ycosb+zcosj)/1.=> xcosa+ycosb+zcosj-p=0 (где р - расст. от О до М).
Угол между плоскостями: cos j=cos(N1,N2)=, где N – нормали плоскостей, =(N1,N2)/sqrt(A12+B12 +C12)sqrt(A22+B22+C22).
Расстояние от точки до плоскости:
D=|Ax0+By0+Cz0+D|/sqrt(A2+B2+C2) где пл. Аx+By+Сz+D=0, М0(x0,y0 ,z0). Расстояние – равно по модулю проекции вектора М1М0 (М0 Î пл.) на нормаль n=(A,B,С). D=|пр.nM1 M0|=|(M1M0 n)/|n||ур.
ПРЯМАЯ НА ПЛОСКОСТИ.
1. Общее уравнение пр. Ах+By+C=0 (1), где A, B одновр. не равны нулю.
Теорема: n(A,B) ортогонален прямой заданной ур-ем (1). Док-во: подставим коорд. т.М0 в ур-е (1) и получим Ах0+By0+C=0 (1’). Вычтем (1)-(1’) получим А(х-х0)+B(y-y0)=0, n(A,B), М0М(х-х0, y-y0). Слева в полученном равенстве записано скалярное произведение векторов, оно равно 0, значит n и M0M ортоганальны. Т.о. n ортоганлен прямой. Вектор n(A,B) называется нормальным вектором прямой. Замеч.: пусть ур-я А1х+B1y+C1=0 и А2х+B2y+C2=0 определяют одну и ту же прямую, тогда найдется такое действительное число t, что А1=t*А2 и т.д. Опр.: если хотя бы один из коэффициентов в ур-ии (1) =0, то ур-е называется неполным. 1. С=0,Ах+By=0 – проходит ч/з (0,0) 2. С=0, А=0,By=0, значит у=0 3. С=0, B=0, Ах=0, значит х=0 4. А=0, By+C=0, паралл. ОХ
5. B=0,Ах+C=0, паралл. OY
2. Уравнение пр. в отрезках:
x/a+y/b=1. Геом.смысл: прямая отсекает на осях координат отрезки а и b. (выводится из уравнения двух точек – x-0/а-0 = y-b/0-b, где точка B=(0,b), А=(а,0)). 3. Каноническое ур: x-x1/e=y-y1/m Пусть на прямой задана точка и напр. вектор прямой (паралл.пр.). Возьмем на прямой произв. точки. q и M1М(х-х1; y-y1), тогда M1M||Sур. 4. Через две точки: x-x1/x2-x1=y-y1/y2-y1 Пусть на прямой даны две точки М1(x1;y1) и М2(x2;y2). Т.к. на прямой заданы две точки, то задан направляющий вектор q(x2-x1; y2-y1) MM1||MM2ур.
5. С углов. коэфф.: y=kx+b. u – угол наклона прямой. Tg угла наклона называется угловым коэффициентом прямой k=tg u. 6. Через точку перп. вектору: A(x-x0)+B(y-y0)=0. MoM_|_N (MoM,N)=0ур.
7. Параметр. ур. прям.: (из канон.)=>
x-x0/m = y-y0/n = t, tR.Система: x=x0+mt y=y0+nt. или: r=r0+st. 8.Через точку в заданн направл.:
n=(cosa,cos). => a+b=90o… n=(cosa, sina). cosb=cos(90-a)=sina => x-x0/cosa = y-y0/sina. y-y0=k(x-x0), k=tga.
Угол между прямыми: tg=|(k2-k1)/1+k1*k2|, где k – угловые коэфф. прямых. Док-во: угол на который нужно повернуть прямую 1 вокруг точки пересечения с 2 до совпадения: a=j(угол между прямыми)+a1.=>tgj=tg(a2-a1)ур.
Расстояние от точки до прямой:
D=|Ax0+By0+C|/sqrt(A2+B2), где прямая Аx+By+С=0, М0(x0,y0). Расстояние – равно по модулю проекции вектора М1М0 (М0 Î прямой) на нормальный вектор n=(A,B). D=|пр.nM1M0|=|(M1M0 n)/|n||ур.
Деление отрезка в соотношении:
Пусть М делит АВ так что АМ/МВ=.Тогда: xm=(x1 +x2)/1+. (тоже для y).
ПРЯМАЯ В ПРОСТРАНСТВЕ
1. Общее уравнение прямой:
Система: A1x+B1y+C1z+D1=0, A2x +b2y+c2z+d2=0 (если A1/A2B1/B2 C1/C2D1/D2 тогда прямая - линия пересечения двух плоскостей).
2. Векторное уравнение прямой:
M0(x0,y0,z0),s(m,n,p) – направ., и произвол. M(x,y,z), r0=OM0(x0,y0,z0) (O – начало коорд.), r=OM=(x,y,z) => M0M=r-r0. MoM || s r-r0=ts => r=r0-ts (tR).
3. Параметрические уравнения: r=r0 +ts, r=(x,y,z), r0=(x0,y0,z0), ts=tm,tn,tp) (урав. 1)=> xi+yj+zk=(x+tm)i+(y0+tn)j+(z0+tp)k => Система: x=x0+mt, y=y0+nt, z=z0+pt.
4. Канонические уравнения прямой: (исключим параметр t из ур. 3)=> x-x0/m +y-y0/n+z-z0/p.
5.Уравнение прямой через 2 точки:
M1, M2, тогда s=M1M2 (направ.)= (x2-x1,y2-y1,z2-z1)=>(урав. 4)=>x-x1/x2-x1 = y-y1/y2-y1=z-z1/z2-z1.
Взаимное расположение (рисунки!):
Условие(У) ||: m1/m2=n1/n2=p1/p2 (т.к. если L1||L2 то s1||s2). У совпадения: s1||s2||M1M2. У пересечения: (s1,s2,M1M2)=0 (т.к. компланарны). У скрещивания: (s1,s2,M1M2) ¹0 (т.к. некомпланарны). У : s1s2 (s1,s2)=0.
Расстояние между скрещ. прям.:
L1 скрещив. с L2. Проведем плоскость P||L2 через прям. L1 и на s1, M1(ÎL1), M2(ÎL2), s2 построим паралл. => p=h=Vпарал./Sосн.= |(M1M2,s1s2)/[s1,s2]|.
Взаимное расположение прям. и пл.:
Плоскость: Ax+By+Cz+D=0, прямая: x-x0/m=y-y0/n=z-z0/p. Тогда: sin= (Am+Bn+Cp)/sqrt(A2+B2+C2)sqrt(m2+n2+p2). Если прям. || пл. тогда Am+ Bn+Cp=0. Если прям ^ пл. тогда A/m=B/n=C/p.
ПЛОСКИЕ ОДК
Опр:
Пусть B=(e1,e2)
– произв. Базис на плоскости. Произвольн.
вектор а можно представить как сумму
векторов коллинеарных e1
и e2.
а=xе1+ye2.
Упорядоченная пара (x,y)
называется
коорд. вектора а в базисе В. Опр:
Базис В*=(е1*,е2*) называется взаимным или
дуальным к базису В, если: еIeJ*=ij=(1,i=j)или
(0,
i¹j).
(-символ
Кронекера.). Тогда упор. пара
(x1*,y1*)-координаты
а в базисе В*.Опр:
Матрица Грамма ![]()
базиса В. |G|=S2паралл. на e1 и е2. Обратная матрица Грамма G*=(1/|G|)*(A11 A21)
т.к. G=(G*)-1| (A12 A22).
Опр:Пусть есть вектор а=xe1+ye2= x*e1*+y*e2* (1). Найдем связь между x,y и x*,y*. Умножим (1) скалярно на е1, затем на е2: xe2e1+ye1e2=x*e1e1*(=1)+y*e1e2*(=0)=>x*=xe1e1+ye1e2, y*=xe2e1+ ye2e2 => (x* y*)=G(x y), (x y)=G*(x* y*). Скаляр. произ в ОДК: ai=xie1+y1e2=x*e1*+yi*e2* => a1a2=(x1e1+y1e2)(x2*e1*+y2*e2*)= x1x2*e1e1*+x1y2*e1e2*+y1x2*e2e1*+y1y2*e2e2*=x1x2*+y1y2*.=> a1a2= (x1 y1)(x2* y2*)\ (символ \ означает что записть должна быть в столбец). = (x1 y1)G(x2 y2)\. (аналогично) a1a2=(x1* y1*)(x2 y2)\=(x1* y1*)G* (x2* y2*)\.
ПРОСТРАНСТВЕННЫЕ ОДК
О пр:
Пусть B=(e1,e2,e3)
произвольный базис. а – произвольный
вектор, его можно представить как сумму
векторов коллинеаных е1,е2,е3. a=xe1+ye2+ze3.
Упорядоченная
тройка (x,y,z)
– координаты
а в базисе В. Матрицей Грамма будет
матрица
G. Опр:
базис В* называется дуальным/взаимным
к В если еiej=dij
(1, i=j,…)(i,j=1,2,3). G*=(1/|G|)*(матрица
трансп. ариф. доп.).|G|=V2паралл.
постр. на е1,е2,е3. Выразим векторы взаимного
через прямой: т.к. е1*e2=0,
e1*e3=0, то
e1*^e2,
e1*^e3,
следовательноб
по св-ву вектр. произв. e1*=[e2,e3].
1=e1e1*=e1[e2,e3]=
(e1,e2,e3)=>
=1/(e1,e2,e3) (аналогично
для е2,е3):
e1*=[e2,e3]/(e1,
e2,e3),
e2*=[e3,e1]/(e1,e2,e3), e3*=
[e1,e2]/(e1,e2,e3).
(аналогично
выражаются е и е*).|G|=(e1,e2,e3)<=
ветекает
из определения об объеме.
пр:
Пусть B=(e1,e2,e3)
произвольный базис. а – произвольный
вектор, его можно представить как сумму
векторов коллинеаных е1,е2,е3. a=xe1+ye2+ze3.
Упорядоченная
тройка (x,y,z)
– координаты
а в базисе В. Матрицей Грамма будет
матрица
G. Опр:
базис В* называется дуальным/взаимным
к В если еiej=dij
(1, i=j,…)(i,j=1,2,3). G*=(1/|G|)*(матрица
трансп. ариф. доп.).|G|=V2паралл.
постр. на е1,е2,е3. Выразим векторы взаимного
через прямой: т.к. е1*e2=0,
e1*e3=0, то
e1*^e2,
e1*^e3,
следовательноб
по св-ву вектр. произв. e1*=[e2,e3].
1=e1e1*=e1[e2,e3]=
(e1,e2,e3)=>
=1/(e1,e2,e3) (аналогично
для е2,е3):
e1*=[e2,e3]/(e1,
e2,e3),
e2*=[e3,e1]/(e1,e2,e3), e3*=
[e1,e2]/(e1,e2,e3).
(аналогично
выражаются е и е*).|G|=(e1,e2,e3)<=
ветекает
из определения об объеме.
С![]()
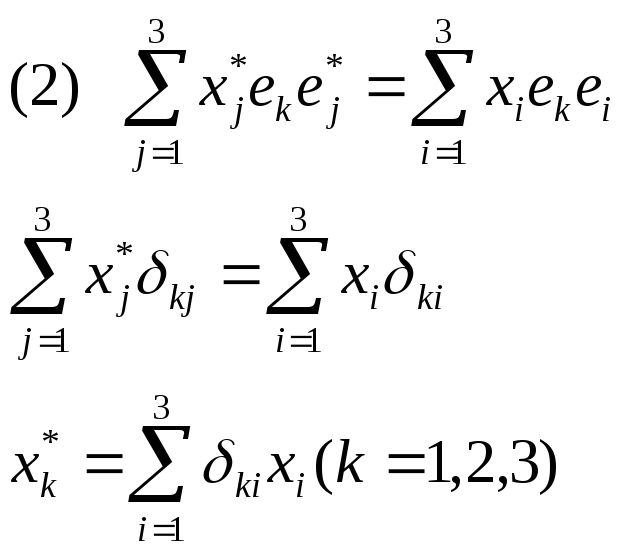 вязь
координат во взаимном б. и прямом:
разложим произв. вектор а во взаимном
и прямом (1), умножим скалярно на ек
(2).
Получаем:
X*=GX,
X=G*X*. Скаляр.
произв:
Разложим вектора x
и y
в басисах В и В* (3). Рассмотрим их скал.
произв. (4). Получаем формулу для вычисл.
скал. произв. в ОДК (5) или в матричн. форме
(6) что равносильно:
xy=XTY*=XTGY
или
xy=(X*)TY=(X*)TG*Y*.
вязь
координат во взаимном б. и прямом:
разложим произв. вектор а во взаимном
и прямом (1), умножим скалярно на ек
(2).
Получаем:
X*=GX,
X=G*X*. Скаляр.
произв:
Разложим вектора x
и y
в басисах В и В* (3). Рассмотрим их скал.
произв. (4). Получаем формулу для вычисл.
скал. произв. в ОДК (5) или в матричн. форме
(6) что равносильно:
xy=XTY*=XTGY
или
xy=(X*)TY=(X*)TG*Y*.
ВЕКТОР. И СМЕШ. ПР. В ОДК
Векторное: Пусть дано (1), тогда по св-вам ОДК (2). Таким образом (3) и (4). Смешанное: Пусть даны три вектора (см. пред.), тогда смеш. произв. (5). Учитывая (2). => (6). Получаем (7)/(8).
ПРЯМАЯ И ПЛОСК. В ОДК
1. Урав. пл. Р, проход. через М0 и ^ вектору n0.Произвол. МР если М0М || PM0M^n(n,M0M)=0 => урав.: (точка в В): a*(x-x0)+b*(y-y0)+c*(z-z0), + наоборот… 2.Урав. прям. L, прох. через М0 и ||q. Произвол. МÎL если М0М||qкоординат. М0М и q пропорциональны => урав: (точка в В): (x-x0)/l=(y-y0)/m=(z-z0)/n, + наоборот… 3. Урав. пл. Р через М0, и || а и b. (a,b неколл.). Произвол. МÎР если М0М, a, b компланарны (M0M,a,b)=0 => урав: (точка и вектора в В): (e1,e2,e3)(опр. коорд. вект)=0 (опр. коорд. вект.), т.к. e1,e2,e3 – некомпланарны. + наоборот… 4. Урав. пл. через 3 точки. (задача сводится к пред., т.е. вектора M1M2, M1M3,M1M, где М – произв. должны быть компл.). 5. Урав. прям. через 2 точки. (урав. аналог. прям. сл.)=>x-x1/x2-x1=…=z-z1/z2-z1. 6. Расстояние от М0 до Р. p(M0,P)= |a*x0+b*y0+c*z0+d|/|n| (где |n|= sqrt(n,n), (n,n)=(N*)TG*N*) + наоб…
ГИПЕРБОЛА.
О

 пр:
ГМТ на плоскости модуль разности
расстояний от которых до двух фиксированных
точек, называемых фокусами, есть величина
постоянная
Канон
урав:
Будем
считать, что фокусы гиперболы находятся
на ОХ на одинаковом расстоянии от начала
координат. |F1F2|=2c,
М – произвольная точка гиперболы. r1,
r2 – расстояния от М до фокусов; |r2-r1|=2a;
a<c;
пр:
ГМТ на плоскости модуль разности
расстояний от которых до двух фиксированных
точек, называемых фокусами, есть величина
постоянная
Канон
урав:
Будем
считать, что фокусы гиперболы находятся
на ОХ на одинаковом расстоянии от начала
координат. |F1F2|=2c,
М – произвольная точка гиперболы. r1,
r2 – расстояния от М до фокусов; |r2-r1|=2a;
a<c;
![]() ,
,
![]()
![]()
![]()
![]()
![]()
x2c2-2a2xc+a2=a2(x2-2xc+c2+y2)
x2(c2-a2)-a2y2=a2(c2-a2)
c2-a2=b2
x2b2-a2y2=a2b2
<![]() -
каноническое ур-е гиперболы (a>0,
b>0).
Свойства:
центр симм.
– (0,0). Оси симм. – оси коорд. Точки перес.
с осями симм. – вершины (А1(-а,0), А2(а,0)).
F1=(c,0),
F2=(-c,0), c=sqrt(a2+b2).
e=c/a (>1). Директрисы:
x1=a/e,
x2=- a/e. Фокальное
св-во:
||F1M|-|F2M||=2a. Директориальное
св-во: |MF1|/p(M,L1)=
|MF2|/p(M2,L2)=e. Оптическое
св-во: луч идущ. из Ф1, оражаясь в М от
гип. идет по Ф2М. Асимптоты: y1=bx/a,
y2=-bx/a.
-
каноническое ур-е гиперболы (a>0,
b>0).
Свойства:
центр симм.
– (0,0). Оси симм. – оси коорд. Точки перес.
с осями симм. – вершины (А1(-а,0), А2(а,0)).
F1=(c,0),
F2=(-c,0), c=sqrt(a2+b2).
e=c/a (>1). Директрисы:
x1=a/e,
x2=- a/e. Фокальное
св-во:
||F1M|-|F2M||=2a. Директориальное
св-во: |MF1|/p(M,L1)=
|MF2|/p(M2,L2)=e. Оптическое
св-во: луч идущ. из Ф1, оражаясь в М от
гип. идет по Ф2М. Асимптоты: y1=bx/a,
y2=-bx/a.
ПАРАБОЛА.
Опр.: ГМТ на плоскости расстояние от которых до фиксированной точки на плоскости, называемой фокусом, равно расстоянию до фиксированной прямой этой плоскости называемой директрисой. Канон. урав.: Пусть фокус параболы находится на оси ОХ, а директриса расположение перпендикулярно оси ОХ, причем они находятся на одинаковом расстоянии от начала координат.
|DF|=p, М – произвольная точка параболы; К – точка на директрисе; МF=r; MK=d; r=sqrt((x-p/2)2+y2); d=p/2+x Приравниваем и получаем:
y2=2px - канон. урав. параболы (p>0). Св-ва: не имеет центра симметрии. Ось симм. – ось абсцисс. Вершина (0,0). Число р–параметр параболы. F(p/2,0) – фокус. Директриса: x=-p/2. Директориал. св-во: |FM|/p(M,L)=e=1(e=c/a). Фокал. св-во: |FM|=p(M,L). Оптич. св-во: луч идущ. из фокуса отражаясь идет || оси параболы.
ЭЛЛИПС
Опр:
ГМТ, сумма растояний от каждой из которых
до двух данных точек этой плоскости
называемых фокусами, есть величина
постоянная, большая чем растояние между
фокусами. Канон.
урав: Пусть
2а – сумма расстояний от точки элипса
до фокусов, а расстояние между фокусами
2с. М(x,y)
– произв.
точка. Из опр. элипса =>
sqrt((x+c)2+y2)+
sqrt((x-c)2+y2)=2a.
 (a>b).
F1=(c,0), F2=(-c,0), c=sqrt(a2-b2).
Эксцентриситет:
e=c/a
(<1). Директрисы:
x1=a/e, x2=-a/e. Фокальное
св-во: |F1M|+|F2M|=2a.
Директ.
св-во: |MF1|/p(M,L1)=|MF2|/
p(M,L2). Вершины:
(a,0),(-a,0),(0,b),(0,-b).
Оптич. св-во: тоже.
(a>b).
F1=(c,0), F2=(-c,0), c=sqrt(a2-b2).
Эксцентриситет:
e=c/a
(<1). Директрисы:
x1=a/e, x2=-a/e. Фокальное
св-во: |F1M|+|F2M|=2a.
Директ.
св-во: |MF1|/p(M,L1)=|MF2|/
p(M,L2). Вершины:
(a,0),(-a,0),(0,b),(0,-b).
Оптич. св-во: тоже.
КОМПЛЕКСНЫЕ ЧИСЛА
Опр: коммплексное число z=x+iy, где x,y – действит. числа, I-мнимая единица (i2=-1). Если x=0, то z-число мнимое число. Если y=0, то z-действ. число, т.е. RC. x=Re(z), y=Im(z). Услов. рав.: z1=z2, если x1=x2 и y1=y2. Понятия больше и меньше для комп. чисел не введено. Два комп. числа отлич. лишь знаком мнимой части называются сопряженными. |z|=r, arg(z)= . Алгебр. запись: z=x+iy. Если рассм. r и , как поляр. коорд М, то x=rcos, y=rsin.=>z=r(cos+ sin). (тригоном. форма). r=|z|=sqrt(x2+y2).=> cos=x/r, sin=y/r, tg=y/x. Получ. =arg(z). Из формулы tg=y/x=> arg(z)=(arctg y/x, (I,IV) +pi (II) –pi (III)). Действия: z1+z2=(x1+x2)+ i(y1+y2). (коммутативность и ассоциативность). z1-z2=(x1-x2)+i(y1-y2). z1z2=(x1x2-y1y2)+i(x1y2+y1x2). => i2=-1(i2=ii=(0+i)(0+i)=(0-1)+i(0+0) =-1). (сочетательный, распределительный, переместительный). z1/z2= (x1x2+y1y2)/(x22+y22)+i((y1x2-x1y2) /(x22+y22)). Теорема Муавра: z= r(cos+isin), zn=rn(cos(n)+isin(n)) z1/n=(корень n-ст.)=sqrt(r)(cos((+ 2c)/n)+isin((+2c)/n)), c=0,1…n-1.
КЛАССИФ. КРИВ. 2-ГО ПОРЯД.
ПРИВЕДЕНИЕ КРИВ. К КАНОН.
Алгебр. кривой 2-го порядка называется кривая, урав. которой в декартовой прямоугольной системе координат (ДПСК) можно представить в виде: (5.1)
Одна и та же кривая в зависимости от расположения относительно ДПСК будет иметь разные урав. Для каждой кривой, определяемой уравнением (5.1), можно подобрать такую новую ДПСК (повернутую), что ее уравнение примет вид (5.2):
Вид кривой, определяемой уравнением, зависит от коэффициентов А. В, С, D, Е, F. 1. АВО - случай центральной кривой. Выделим полные квадраты:
5.2 примет вид
Перейдем теперь к новой ДПСК – Х’О’У’, которая получается из исходной ДПСК ХОУ паралл. переносом. Начало ДПСК Х’О’У’ поместим в т. О (,). Тогда точка М, имеющая относительно ДСПК ХОУ координаты (Х,У) будет иметь относительно ДПСК Х’О’У’ координаты x’=x-, y’=y-, а уравнение (5.4) в ДПСК Х’O’У’ запишется (5.5):
(для удобства в дальнейшем вместо Х’ и У’ будем писать Х и У).
1.1. AB > 0 - эллиптический тип.
виде (5.6)
В этом урав., не нарушая общности, можно считать a2b2 в противном случае нужно ДПСК повернуть на 90°. Кривая, уравнение которой относительно некоторой ДПСК имеет уравнение (5.6) называется эллипсом. б) Н=0, единственная точка (0,0) в) Н<0, мнимый элипс
1.2. AB < 0 -гиперболический тип.
а) А>0, В<0, Н > 0 .
Кривая, уравнение которой относительно некоторой ДПСК имеет вид (5.7) называется гиперболой
б) Н=0, вырожденная гипербола
2. AB.= 0 - параболический тип.
2.1. А = 0 ( В 0), С0.
В этом случае (5.2) имеет вид:
Выделив полный квадрат, преобразуем это уравнение:
нение перепишется в виде (y-)2=2p(x-). Перейдя теперь, как и в случае 1 к новой ДПСК Х’O’У’ получим: (y’)2=2px’. Опустим для удобства штрихи: y2=2px (5.8)
Кривая, урав. которой относительно некоторой ДПСК имеет вид (5.8), называется параболой. В урав. (5.8), не нарушая общности, можно считать р > 0 в противном случае нужно повернуть ДПСК на 180°. Случай В = О, D0, очевидно, сводится к предыдущему, если повернуть ДПСК на 90°. 2.2. А=0, В0б С=0 а) H>0, вырожденная парабола. б) Н<0, мнимые || прямые в) H=0, сопадающие прямые.
