
шпоргалка / шпора 39
.doc|
№39 Пусть ф-ции P(x,y),Q(x,y) и их частные производные dP/dy, dQ/dx непрерывны, замкнуты, ограничены односвязной областью Д, тогда следующие 4 условия эквивалентны: 1)
замкнутый контур Д. 2) 3) Pdx+Qdy=dU, U – однозначная ф-ция, определенная в области Д. \ 4) dP/dy=dQ/dx в области Д. Доказательство:
где
Т.к. у ф-ции U существуют непрерывные частные произодные, то она дифиренцируема.
Нахождение ф-ции по ее полному дифференциалу. Первый способ: U(x,y)-?; dU=Pdx+Qdy; Pdx+Qdy*dQ/dx=dP/dy
Второй способ:
{
№18
Пусть f(x)
определена на
Пусть
Если этот lim существует и конечен, то говорят, что НИ-1 сходится. Если не существует или бесконечен, то расходится.
Свойтсва НИ-1.
Если
Если
Исследование на сходимость. Т1:
Пусть ф-ции f(x)
и g(x)
сходится
расходится
Предельный признак сравнения для НИ-1. Т2:
Пусть При
k=1
Т3:
Если
|
1.Комплексные числа в алгебраической, тригонометрической и показательной формах 2.Многочлены и их делимость. Теорема Безу. Основная теорема алгебры. 3. Рациональные дроби и их разложение на сумму простейших дробей. 4. Первообразная. Неопределенный интеграл и его свойства. 5. Замена переменной в неопределенном интеграле. 6. Интегрирование по частям. Основные классы функций, интегрируемых по частям. 7. Интегрирование рациональных функций. 8. Интегрирование тригонометрических функций. 9. Интегрирование иррациональных функций. 10. Понятие определенного интеграла и его геометрический смысл.11. Свойства определенного интеграла. 12. Определенный интеграл с переменным верхним пределом. 13. Замена переменной в определенном интеграле. 14. Интегралы от четных, нечетных и периодических функций15. Вычисление площадей плоских фигур16. Вычисление длины дуги с помощью определенного интеграла.17. Вычисление объемов пространственных тел с помощью определенного интеграла.18. Несобственные интегралы первого рода, их свойства и вычисление19. Несобственные интегралы второго рода.20.Квадратурные формулы прямоугольников, трапеций и Симпсона. 21. Понятие функции нескольких переменных. 22. Частные производные . 23 . Дифференцируемость функции нескольких переменных. 24. Частные производные сложной функции. 25. Неявные функции и их дифференцирование. 26. Геометрический смысл полного дифференциала. 27. Частные производные высших порядков. 28. Формула Тейлора для функции нескольких переменных. 29. Локальный экстремум функции нескольких переменных. 30. Условный экстремум функции нескольких переменных. 31. Интегралы по фигуре от скалярной функции, их свойства 32. Криволинейный интеграл первого рода. 33. Двойной интеграл. 34. Тройной интеграл. 35. Поверхностный интеграл первого рода. 36. Интегралы по ориентированной фигуре от векторной функции и их свойства. 37. Криволинейный интеграл второго рода, его механический смысл 38. Формула Грина. 39. Условия независимости криволинейного интеграла второго рода от пути. 40. Поверхностный интеграл второго рода, его физический смысл 41. Скалярные поля. Производная скалярного поля по направлению. Градиент.42. Векторные поля. Поток векторного поля. Дивергенция. Формула Остроградского.43. Циркуляция и ротор векторного поля. Формула Стокса.44. Операторы Гамильтона и Лапласа.45 Потенциальное векторное поле и его свойства.46.Соленоидальное векторное поле. Гармоническое векторное поле.
Определение:
Если
Главное значении.
Главным
значением
Если
|
№33
y-трапецевидная
область Д.
x-трапецевидная
область Д
Пусть в основании цилиндрического тела лежит y-трапецевидная область.
области более сложного вида разбиваются на сумму Замена переменной в двойном интеграле. Рисунки: 1) ось v (вверх) – 0 – u кружок, а в нём D’ 2) ось y – 0 – x вытянутый вверх эллипс, в нём D
Свойства
P1: x(u,v), y(u,v) P2: x(u+∆u,v), y(u+∆u,v)
I – Якобиан(Якоби) Модуль I – коэффициет растяжения площади в т. с координатами u и v при отображении D на D’.
Вычисление в полярной сист координат.
a)
b
c)
|






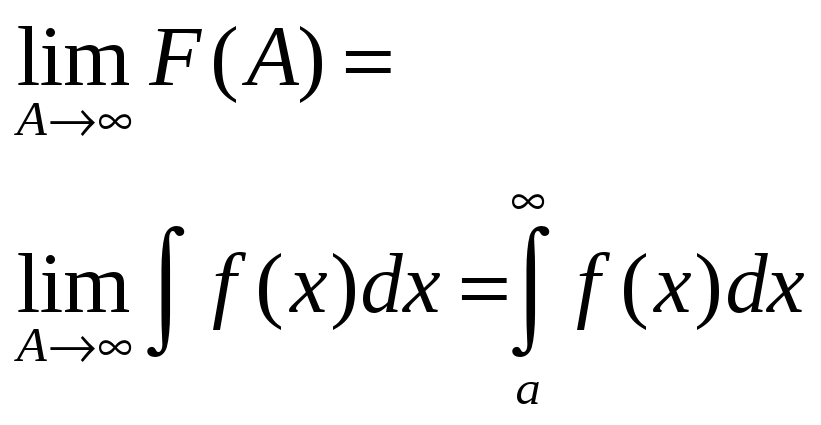

 сходится и
сходится и
 ;
VP-Value
principul
;
VP-Value
principul ;
;

 для
y-трапецевидной
области
для
y-трапецевидной
области для
x-
для
x- (*)
(*)










 )
)

