24.Понятие о уравнении кривой на плоскости. Уравнение прямой.

25.Различные уравнения прямых на плоскости. Взаимное расположение прямых.

26.Нормированное уравнение прямой, на плоскости. Взаимное расположение прямых.

Пусть дана прямая l. Проведем через начало координат прямую n, перпендикулярную l. Пусть Р - точка пересечения прямых. Возьмем единичный вектор .

Выразим уравнение l через два параметра: и угол . Пусть М(х,у) принадлежит l. Тогда проекция на ось, определяемую вектором, равна р, то есть при условии пр_n, так как единичный вектор, то согласно определению скалярного произведения пр_n,=. Так как, а вектор, то скалярное произведение имеет вид

.

Следовательно, точка М принадлежит прямой l означает, что координаты этой точки удовлетворяют уравнению

(1.8)

Это и есть нормированное уравнение прямой l.

Пусть теперь имеем общее уравнение прямой l:

l: Ах + Ву + С = 0

l:

Отсюда

tA = Cos, tB = Sin, tC = -p.

Учитывая, что t²A² + t²В² = Cos² + Sin² = 1

получаем t²(A² + В²) = 1(1.9)

или -нормирующий множитель.

Следовательно, чтобы получить из общего уравнения прямой

Ах + Ву + С = 0

нормированное уравнение (1.8) следует умножить его на нормирующий множитель (1.9), знак которого противоположен С.

27.Уравнение пучка прямых на плоскости.

Пучком прямых называется совокупность всех тех прямых на плоскости, которые проходят через некоторую точку О плоскости или параллельны между собой. Точку О называют центром или носителем П. Если заданы уравнения двух некоторых прямых П.:

A₁x + B₁y + C₁ = 0 и A₂x + В₂у + С₂ =0,

то уравнение П. прямых можно представить в виде:

l(A₁x + B₁y + C₁) +m(A₂x + В₂у + С₂) = 0,

где параметры l и m не обращаются одновременно в нуль и принимают любые значения. Пучком плоскостей называется совокупность всех плоскостей, проходящих через некоторую прямую (ось пучка) или параллельных между собой.

28.Приведение общего уравнения кривой второго порядка к каноническому виду.

29.Классификация кривых второго порядка и их канонические уравнения.

30.Эллипс и его св-ва:

Кривая второго порядка наз. эллипсом если коэффициенты А и L имеют одинаковые знаки

Аx²+Cy²=

ур.-е

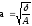
наз. канонич. ур.-ем эллипса, где При а=в представляет собой ур-е окружности х²+y²=а²

Точки F₁(-c,0) и F₂(c,0) - наз. фокусами эллипса а.

Отношение =с/а наз. его эксцентриситетом (0<=<=1)

Точки A₁,A₂,B₁,B₂ -вершины эллипса.

Св-во:Для любой точки эллипса сумма расстояний этой точки до фокусов есть величина постоянной, =2а.

31. Гипербола и ее св-ва.

Кривая 2го порядка наз. гиперболой, если в ур-ии Ax²+Cy²=, коэффициент А и С имеют противоположные знаки, т.е. А*С<0

б) Если >0, то каноническое ур-е гиперболы примет вид: x²/a²-y²/b²=1, F1(c,o) и F₂(-c,0) - фокусы ее, >0, =c/a - эксцентриситет.

Св-во:для любой точки гиперболы абсолютная величина разности ее расстояний до фокусов есть величина постоянная = 2а.

б) если =0, ур-е примет вид x²/a²-y²/b²=0, получаем 2 перекрестные прямые х/ау/b=0

в) если <0, то x²/a²-y²/b²=-1 - ур-е сопряженной гиперболы.