Вариант 7

Задача 1

Для приведенной электрической схемы электропередачи определить коэффициент запаса устойчивости для случаев:

а) при отсутствии АРВ;

б) при АРВ пропорционального действия;

в) при АРВ сильного действия.

Расчет выполнить в относительных единицах с приближенным приведением к основной ступени напряжения.

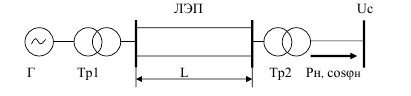
Рисунок - Схема электропередачи

Параметры схемы:

Генератор Г:

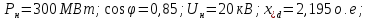
ТрансформаторТр1×2:

ТрансформаторТр2×2:

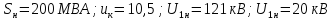
ЛЭП:

Передаваемая мощность от генератора на шины приемной системы:

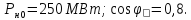
Решение

Подготовка исходных данных:

Примем за базисные условия:

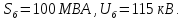
Рассчитаем сопротивления элементов схемы:

Генератор:

- синхронное

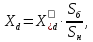
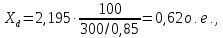
- переходное

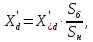
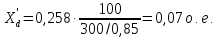
Трансформаторы Тр1 и ТР2:

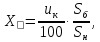
Линии:

Относительные значения передаваемой мощности от генератора на шины приемной системы:

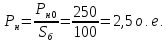
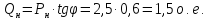
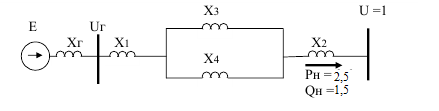
Рисунок 2- Схема замещения электропередачи

2. Определение запасов устойчивости системы

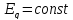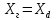а) При отсутствии АВР предел передаваемой мощности определяется из условия постоянства синхронной ЭДС при и

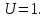
Суммарное сопротивление электропередачи 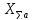равно:

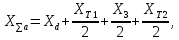
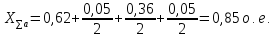
Найдем синхронную ЭДС:

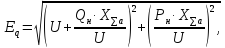
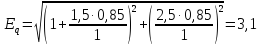
Предел передаваемой мощности:

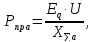
Коэффициент запаса статической устойчивости:

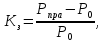
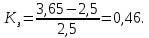
б) При установке на генераторах АВР пропорционального действия предел передаваемой мощности и устойчивости можно приближенно определить исходя из постоянства ЭДС 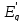за переходным сопротивление

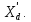
В этом случае суммарное сопротивление электропередачи 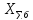равно:

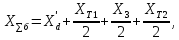
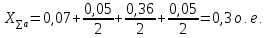
Найдем ЭДС:

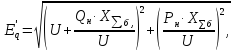
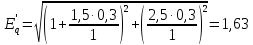
Предел передаваемой мощности:

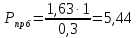
Коэффициент запаса статической устойчивости:

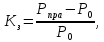
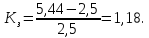
в) АРВ сильного действия в зависимости от настройки может обеспечивать постоянство напряжения либо на выводах генератора, либо за трансформатором Тр1 в начале линии. Определим предел устойчивости, принимая напряжение генератора . В этом случае сопротивление генератора принимается равным нулю.

В этом случае суммарное сопротивление электропередачи равно:

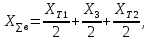
Найдем ЭДС:

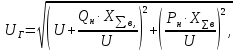
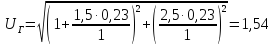
Предел передаваемой мощности:

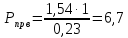
Коэффициент запаса статической устойчивости:

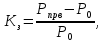
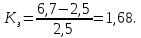
Задача 2

Определить величину максимальной мощности, передаваемую станцией С1, построить график зависимости

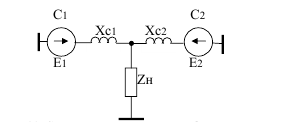
Рисунок 3- Система из двух станций, работающая на нагрузку, которая задана постоянным сопротивлением

Исходные данные в относительных единицах:

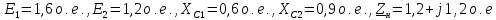
Решение

Если схема замещения между источниками состоит из активных и индуктивных сопротивлений, а нагрузка представлена постоянными сопротивлениями, которые не зависят от тока и напряжения, то ток и мощность передающей станции определяются через собственные и взаимные проводимости ветвей системы. Вычислив для передающей станции собственные и взаимные проводимости сразу можно записать зависимость 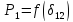в виде:

Максимум этой характеристики

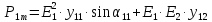
дает значение действительного предела мощности.

Собственное и взаимное сопротивления для станции 1:

тогда

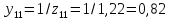
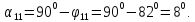
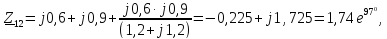
тогда

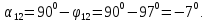
Подставляя найденные значения в формулу для получим:

Задаваясь значениями угла 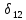вычисляем 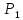, результаты заносим в таблицу1.

Таблица 1

𝜹, град	-7	0	30	60	90	120	150
Р1 о.е	0,290	0,423	0,948	1,297	1,379	1,164	0,717

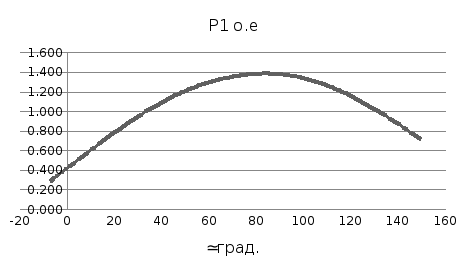
Рисунок 4- Угловая характеристика мощности генератора Г1