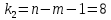Расчётно-графическая работа по дисциплине «Эконометрика»
.docxМИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное бюджетное образовательное
учреждение высшего образования
«НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ
ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
Кафедра маркетинга и сервиса
Расчётно-графическая работа по дисциплине
ЭКОНОМЕТРИКА
Выполнил:
студент III курса, специальность «Производственный менеджмент»
группа ЭКз-41, № зачет. книжки
Преподаватель: Щеколдин Владислав Юрьевич
Должность: доцент, кандидат технических наук
Оценка: ______________ Дата: ________________________
Подпись: _____________________________________________
Новосибирск, 2017 г.
Задание № 1

Вышеуказанный график позволяет сделать предположение, что связь между стоимостью основных производственных фондов и среднесуточной производительности положительная и линейная.
Задание № 2
Парный
коэффициент корреляции для линейной
формы связи определяется по формуле:
 ,
где средние величины рассчитываются
по следующим формулам:
,
где средние величины рассчитываются
по следующим формулам:
-
 ;
; -
 ;
; -
 .
.
Средние квадратные отклонения:
-
 ;
; -
 ;
;
-
 ;
; -
 ;
; -
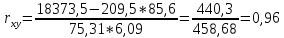 .
.
Вывод:
коэффициент корреляции
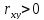 ,
следовательно, связь положительная.
Согласно «таблице Чеддока» связь очень
высокая.
,
следовательно, связь положительная.
Согласно «таблице Чеддока» связь очень
высокая.
Чтобы оценить значимость коэффициента корреляции необходимо сформулировать гипотезы:
-
 коэффициент
корреляции незначим;
коэффициент
корреляции незначим; -
 коэффициент
корреляции значим.
коэффициент
корреляции значим.
Для проверки гипотезы используются t-критерии Стьюдента
-
 .
.
По
таблице распределения Стьюдента при
доверительной вероятности 0,95 или уровня
значимости
 и числе степеней свободы
и числе степеней свободы
 .
.
 =2,306.
=2,306.
 ,
т. к. 9,71
,
т. к. 9,71
 2,306.
2,306.
В данном случае должна быть принята альтернативная гипотеза, которая будет характеризовывать значимость коэффициента корреляции.
Задание № 3
Линейная функция характеризующая взаимосвязь между факторами X и Y может быть представлена уравнением парной линейной регрессии:
Метод
наименьших квадратов дает следующую
систему нормальных уравнений для
определения параметров
 и
и
 .
.
-
 ;
; -
 ;
; -
 .
.
Вычитая одно уравнение из другого получаем:
Следовательно:
-
 ;
; -
 .
.
Уравнение регрессии примет вид:
-
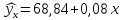 .
.
Вывод:
коэффициент регрессии
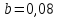 характеризует,
что с ростом стоимости основных
производственных фондов на 1 тыс. руб.
среднесуточная производительность
увеличится на 0,08 тонн.
характеризует,
что с ростом стоимости основных
производственных фондов на 1 тыс. руб.
среднесуточная производительность
увеличится на 0,08 тонн.
Задание № 4
Значимость
параметров модели предполагает оценку
значимости параметров
 и
и
 .
.
Оценим значимость коэффициентов регрессии:
-
 коэффициент
регрессии
коэффициент
регрессии
 незначим;
незначим; -
 коэффициент
регрессии
коэффициент
регрессии
 значим.
значим.
 ,
где:
,
где:
-
 ;
; -
 .
.
Найдем данные значения:
-
 ;
; -
 ;
; -
 .
.
 .
.
Вывод:
 ,
т.к. 4
,
т.к. 4 2,306
, следовательно коэффициент регрессии
2,306
, следовательно коэффициент регрессии
 значим.
значим.
Оценим
значимость параметра
 :
:
 коэффициент
регрессии
коэффициент
регрессии
 незначим;
незначим;
 коэффициент
регрессии
коэффициент
регрессии
 значим.
значим.
 ,
где:
,
где:
-
 ;
; -
 .
.
Найдем данные значения:
-
 ;
; -
 .
.
Вывод:
 ,
т.к. 20,37
,
т.к. 20,37 2,306
, следовательно коэффициент регрессии
2,306
, следовательно коэффициент регрессии
 значим.
значим.
Для значимых коэффициентов можно построить доверительные интервалы.
Доверительный
интервал параметра
 :
:
-
Предельная ошибка параметра
 :
:
 .
. -
Доверительный интервал параметра
 :
:
 ;
;
 ;
;
 .
.
Доверительный
интервал параметра
 .
.
-
Предельная ошибка параметра
 :
:
 .
. -
Доверительный интервал параметра
 :
:
 ;
;
 ;
;
 .
.
Задание № 5
Оценим значимость уравнения регрессии в целом с помощью F-критерия Фишера.
Фактическое
значение
 определяется по формуле:
определяется по формуле:
 .
.
Табличное
значение
 по
таблице значений F-критерия Фишера при
по
таблице значений F-критерия Фишера при
 равно
равно
 .
.
Вывод:
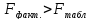 ,
т. к.
,
т. к.
 ,
что свидетельствует о статистической
значимости уравнения регрессии в целом.
,
что свидетельствует о статистической
значимости уравнения регрессии в целом.
Задание № 6
Анализ выполняется при сравнении фактического и табличного значений F-критерия Фишера.

|
Вариация результата, y |
Число степеней свободы |
Сумма квадратов отклонений, S |
Дисперсия
на одну степень свободы,
|
|
|
|
Общая |
|
370,4 |
41,16 |
15,9 |
5,32 |
|
Факторная |
|
363,02 |
363,02 |
||
|
Остаточная |
|
182,64 |
22,83 |
-
Суммы квадратов отклонений:
-
Общая:
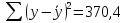 ;
; -
Факторная:
 ;
; -
Остаточная:
 .
.
-
Дисперсия на одну степень свободы:
-
Общая:
 ;
; -
Факторная:
 ;
; -
Остаточная:
 .
.
-
Фактическое значение F-критерия Фишера:
-
 .
.
Вывод:
сравнивая
 и
и
 ,
можно сделать вывод о том, что нулевая
гипотеза
,
можно сделать вывод о том, что нулевая
гипотеза
 должна быть отклонена и принята
альтернативная гипотеза
должна быть отклонена и принята
альтернативная гипотеза
 о статистической значимости уравнения
регрессии в целом и показателя тесноты
связи между стоимости ОПФ и среднесуточной
производительности, так как они
статистически надежны и сформировались
под систематическим действием изучаемых
факторов. Вероятность того, что допускаются
ошибки при отклонении нулевой гипотезы,
не превышают 5%, и это является достаточно
малой величиной.
о статистической значимости уравнения
регрессии в целом и показателя тесноты
связи между стоимости ОПФ и среднесуточной
производительности, так как они
статистически надежны и сформировались
под систематическим действием изучаемых
факторов. Вероятность того, что допускаются
ошибки при отклонении нулевой гипотезы,
не превышают 5%, и это является достаточно
малой величиной.
Задание № 7
При =349
точечным прогнозом будет являться
следующее уравнение –
=349
точечным прогнозом будет являться
следующее уравнение –
 .
.
Задание № 8
 ,
где:
,
где:
-
 ;
; -
 (
( ;
; -

Задание № 9

Задание № 10
Коэффициент
корреляции
 ,
следовательно, связь положительная.
Согласно «таблице Чеддока» при значении
,
следовательно, связь положительная.
Согласно «таблице Чеддока» при значении связь считается очень высокой.
связь считается очень высокой.
Коэффициент
регрессии
 характеризует,
что среднесуточная производительность
увеличится на 0,08 тонн с ростом стоимости
основных производственных фондов на 1
тыс. руб.
характеризует,
что среднесуточная производительность
увеличится на 0,08 тонн с ростом стоимости
основных производственных фондов на 1
тыс. руб.
При
оценке значимости коэффициентов
регрессии было установлено, что
коэффициенты регрессии
 и
и
 значимы (
значимы ( )
т. к.
20,37
)
т. к.
20,37 2,306
и 4
2,306
и 4 2,306
соответственно.
2,306
соответственно.
При
оценке значимости уравнения регрессии
в целом с помощью F-критерия Фишера, был
сделан вывод о том, что уравнение
регрессии в целом статистически значимо,
поскольку.
 (
( ).
).
После
проведения дисперсионного анализа,
можно прийти к выводу о том, что нулевая
гипотеза
 должна быть отклонена и принята
альтернативная гипотеза
должна быть отклонена и принята
альтернативная гипотеза
 о статистической значимости уравнения
регрессии в целом и показателя тесноты
связи между стоимости ОПФ и среднесуточной
производительности, так как они
статистически надежны и сформировались
под систематическим действием изучаемых
факторов. Вероятность того, что допускаются
ошибки при отклонении нулевой гипотезы,
не превышают 5%, и это является достаточно
малой величиной.
о статистической значимости уравнения
регрессии в целом и показателя тесноты
связи между стоимости ОПФ и среднесуточной
производительности, так как они
статистически надежны и сформировались
под систематическим действием изучаемых
факторов. Вероятность того, что допускаются
ошибки при отклонении нулевой гипотезы,
не превышают 5%, и это является достаточно
малой величиной.







 1
1