23.Циркуляция вектора индукции магнитного поля

Закон полного тока гласит о том, что линейный интеграл по замкнутому контуру l от напряженности магнитного поля равен полному току, протекающему сквозь сечение, ограниченное этим контуром.

Магнитное поле соленоида

24. Поток вектора напряженности магнитной индукции

Поток вектора магнитной индукции, пронизывающий площадку S - это величина, равная:

Поток вектора магнитной индукции (магнитный поток) измеряется в веберах (Вб)

Магнитный поток - величина скалярная.

Поток вектора магнитной индукции (магнитный поток) равен числу линий магнитной индукции, проходящих сквозь данную поверхность.

Поток вектора магнитной индукции (магнитный поток) сквозь произвольную замкнутую поверхность равен нулю:

Теорема Гаусса для магнитного поля

25. Работа по перемещению проводника и контура с током в магнитном поле.

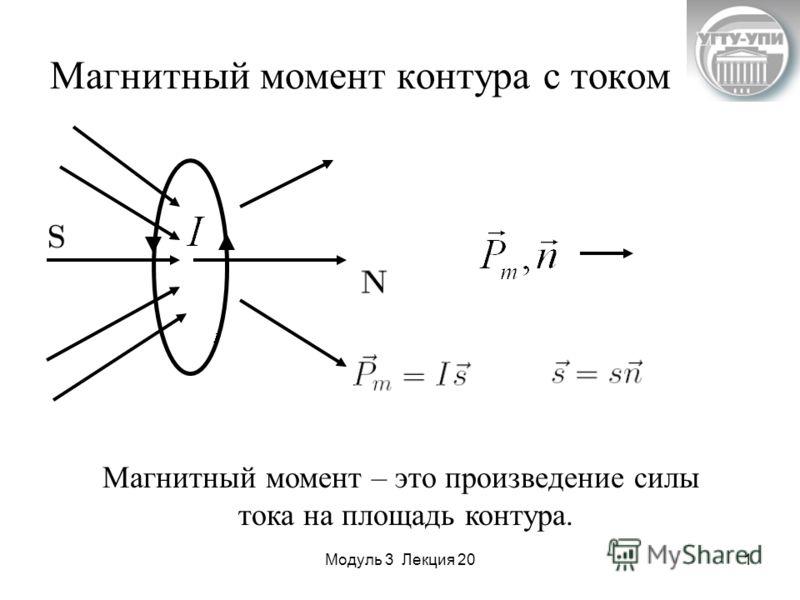
26.Контур с током в магнитном поле

Магнитный момент контура с током

27. Магнитное поле движущегося заряда

Каждый проводник с током создает в ок­ружающем пространстве магнитное поле. Электрический же ток представляет собой упорядоченное движение электрических зарядов. Поэтому можно сказать, что лю­бой движущийся в вакууме или среде за­ряд создает вокруг себя магнитное поле. В результате обобщения опытных данных

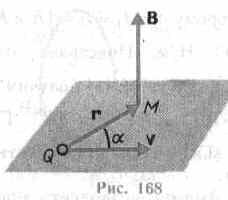
был установлен закон, определяющий по­ле В точечного заряда Q, свободно движу­щегося с нерелятивистской скоростью v. Под свободным движением заряда по­нимается его движение с постоянной ско­ростью. Этот закон выражается формулой

где r — радиус-вектор, проведенный от за­ряда Q к точке наблюдения М (рис. 168). Согласно выражению (113.1), вектор В направлен перпендикулярно плоскости, в которой расположены векторы v и г, а именно: его направление совпадает с на­правлением поступательного движения правого винта при его вращении от v к г. Модуль магнитной индукции (113.1) вычисляется по формуле

где а — угол между векторами v и r.

Сравнивая выражения (110.1) и (113.1), видим, что движущийся заряд по своим магнитным свойствам эквива­лентен элементу тока: Idl=Qv.

Действие магнитного поля на движущийся заряд

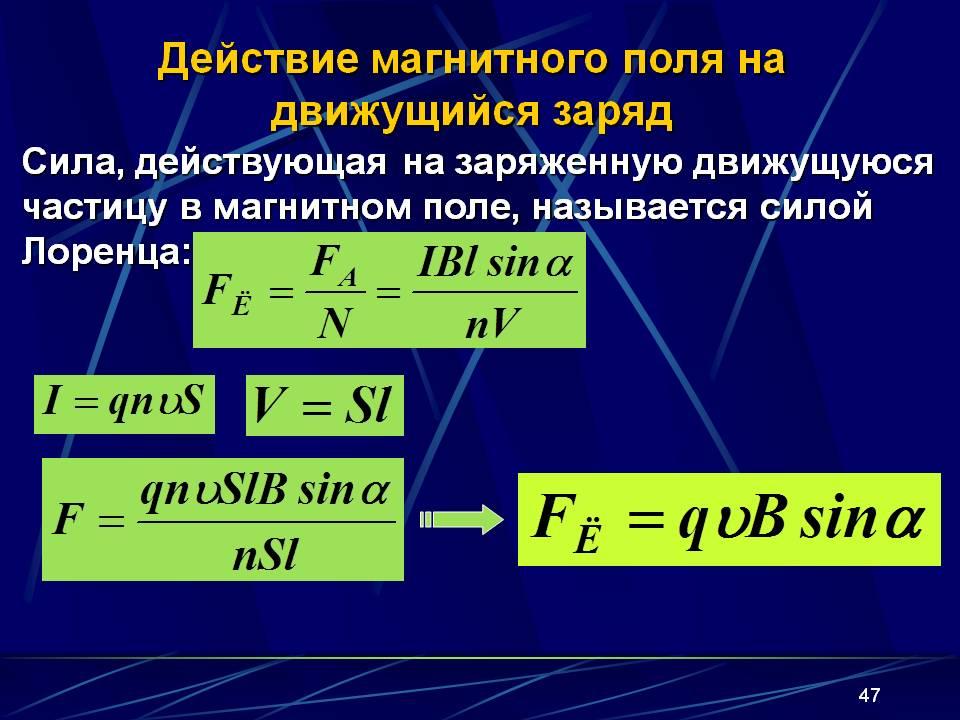
Сила Лоренца

Сила Лоренца – сила, действующая на точечную заряженную частицу, движущуюся в магнитном поле. Она равна произведению заряда, модуля скорости частицы, модуля вектора индукции магнитного поля и синуса угла между вектором магнитного поля и скоростью движения частицы.

28.Движение заряженных частиц в магнитном поле

{\displaystyle \mathbf {M} ={\frac {\mathbf {p_{m}} }{V}}}

29. Магнитные моменты электронов и атомов

Намагни́ченность — векторная физическая величина, характеризующая магнитное состояние макроскопического физического тела. Обозначается обычно М. Определяется как магнитный момент единицы объёма вещества:

Магнитное поле в веществе

Все вещества являются магнетиками – при помещении их во внешнее магнитное поле они создают свое магнитное поле, то есть намагничиваются:

 

Рис. 9.5

Качественно возникновение собственного магнитного поля магнетика можно пояснить на основе гипотезы Ампера существовании внутри молекул молекулярных токов (микротоков). Произведение кругового тока на обтекаемую им площадь называютмагнитным моментом (рис. 9.5) . Модуль вектораДля характеристики магнетика вводятвектор намагничивания , который равен векторной сумме магнитных моментоватомов, находящихся в единице объема вещества:

Ориентация магнитных моментов атомов во внешнем магнитном поле и создает не равное нулю магнитное полевещества и соответственно(рис. 9.6).

Рис. 9.6

Для удобства описания магнитных полей в среде вводится вектор напряженности магнитного поля

В случае вакуума = 0,и поэтому

Для однородных изотропных магнетиков из опыта установлена следующая формула связи векторов и:

где χ – магнитная восприимчивость вещества.