Билеты 1 курс 1 семестр экологи

БИЛЕТ №1 (ПОНЯТИЕ ФУНКЦИИ, СПОСОБЫ ЗАДАНИЯ,ОСНОВНЫЕ СВОЙСТВА)

Функция: зависимость переменной у от переменной х, если каждому значению х соответствует единственное значение у, где переменная х- независимая переменная или аргумент, а переменная у зависимая переменная.

Способы задания функции: табличный способ, аналитический способ, графический способ

Основные свойства функции:

1)Область определения функции

2)Промежутки возрастания и убывания

3)Нули функции

4)Четность-нечетность

5)Периодичность функции

БИЛЕТ №2 (ПОНЯТИЕ ОКРЕСТНОСТИ ТОЧКИ, ВНУТРЕННИЕ И ГРАНИЧНЫЕ МНОЖЕСТВА)

Окрестностью точки называется интервал, не содержащий точку. См.рис.

Внутренние и граничные точки множества

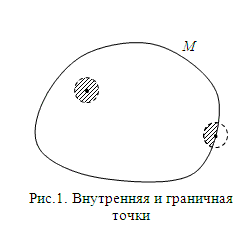Закрашенная точка является внутренней точкой множества М. Закрашенная наполовину точка является граничной точкой множества М.

БИЛЕТ №3 (ОПРЕДЕЛЕНИЕ ПРЕДЕЛА ФУНКЦИИ В ПРЕДЕЛЬНОЙ ТОЧКЕ( ПО КОШИ))

БИЛЕТ №4 (ПОНЯТИЕ БЕСКОНЕЧНОГО ПРЕДЕЛА)

БИЛЕТ №5 (ОСНОВНЫЕ СВОЙСТВА ПРЕДЕЛОВ:ЕДИНСТВЕННОСТЬ,МОНОТОННОСТЬ,ОДНОРОДНОСТЬ,АДДИТИВНОСТЬ)

БИЛЕТ №6 (ТЕОРЕМА О СЖАТОЙ ФУНКЦИИ, ПРЕДЕЛ СЛОЖНОЙ ФУНКЦИИ)

Теорема о сжатой функции:

Предел сложной функции:

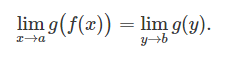
БИЛЕТ №7 (ТЕХНИКА ВЫЧИСЛЕНИЯ ПРЕДЕЛА.ТИПЫ НЕОПРЕДЕЛЁННОСТЕЙ)

Lim f(x)=(f(x0)=A)=A x->x0 Виды неопределенностей: 0/0 ; бесконечность/бесконечность ; бесконечность – бесконечность ; 1^бесконечноть; 0^0

БИЛЕТ №8 (БЕСКОНЕЧНО МАЛЫЕ, ИХ КЛАССИФИКАЦИЯ И СВОЙСТВА . СПИСОК ОСНОВНЫХ ЭКВИВАЛЕНТНЫХ БЕСКОНЕЧНО МАЛЫХ)

Бесконечно малые Числовая функция или последовательность, которая стремится к нулю.

Б.М.- функция альфа (х) называется бм при х->х0 , если lim альфа (х)=0 х->x0 Классификация: ] альфа х и бетта х – б.м. 1. Две б м называются однопорядковыми если предел их отношений равен числу не равному 0 lim альфа (х)/бетта(х) = А неравно 0 и неравно бесконечности х->x0 Если альфа (х) и бетта(Х) одного порядка кратко это можно записать альфа(х)=О (бетта(х) О-символ Ландау 2. Говорят что альфа(Х) более выского порядка чем бетта если предел их отношений равен нулю lim альфа (х)/бетта (Х) = О x->x0 краткая запись: альфа(х)=О (бетта(х) 3.говорят что альфа (х) эквивалента (полная одинаковость) бетта (х) если предел их отношений равен 1 lim альфа (х)/бетта(х)=1 х->x0 альфа (Х) эквивалента бетта(х) СВОЙСТВА БМ:

БИЛЕТ №9 (БЕСКОНЕЧНО БОЛЬШИЕ И ИХ КЛАССИФИКАЦИИ)

БИЛЕТ №10 (ПЕРВЫЙ И ВТОРОЙ ЗАМЕЧАТЕЛЬНЫЕ ПРЕДЕЛЫ И ИХ ОБОБЩЕНИЕ)

Первым замечательным пределом называется предел вида

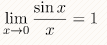(sin (x) эквивалентен Х)

Следствия первого замечательного предела

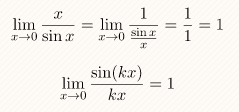
Второй замечательный предел призван помогать избавляться от неопределенности вида 1^ ∞ и выглядит он так :

1.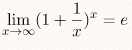2. Lim (1+x) ^1/х = е 3. Lim (1+1/n) ^n = e x->0 n->+ бесконечность Обобщение замечательных пределов: пусть альфа (х) – бм при х стремящемуся к х0 тогда

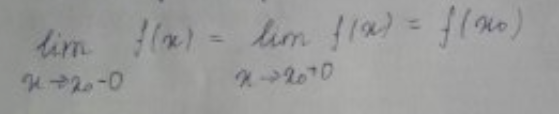
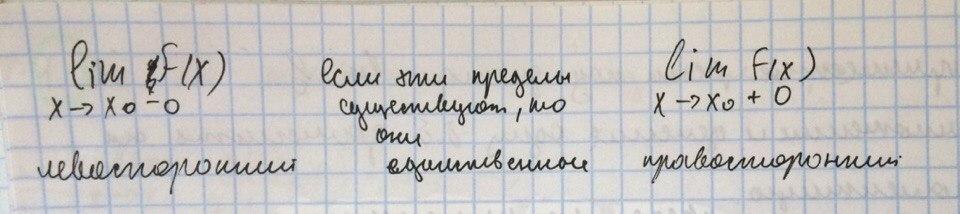
БИЛЕТ №11 (ОПРЕДЕЛЕНИЕ ОДНОСТОРОННЫХ ПРЕДЕЛОВ ФУНКЦИИ . НЕПРЕРЫВНОСТЬ В ТОЧКЕ. НЕПРЕРЫВНОСТЬ В ОБЛАСТИ.) Односторонний предел – предел числовой функции подразумевает приближение к предельной точке с одной стороны. Непрерывность в точке – функция f(x) называется непрерывной в точке x0 если непрерывность в области

БИЛЕТ №12 (ОСНОВНЫЕ СВОЙСТВА ФУНКЦИЙ,НЕПРЕРЫВНЫХ НА ОТРЕЗКЕ)

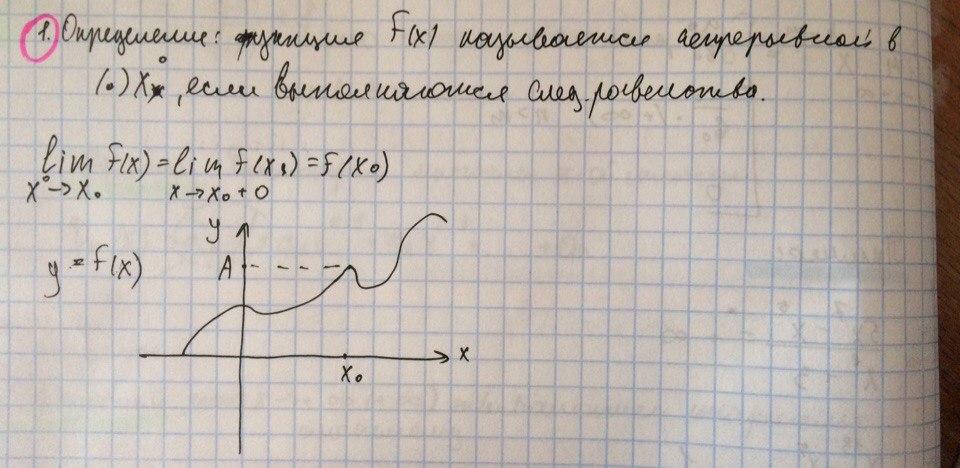
БИЛЕТ №13 (ТОЧКИ РАЗРЫВА И ИХ КЛАССИФИКАЦИЯ. ГЕОМЕТРИЧЕСКИЙ ОБРАЗ РАЗРЫВОВ)

Точка , в которой нарушено хотя бы одно из трех условий непрерывности функции, а ээименно:

1. функция  определена в точке и ее окрестности;

2. существует конечный предел функции 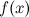 в точке ;

3. это предел равен значению функции в точке , т.е.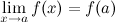 

называется точкой разрыва функции.

БИЛЕТ №14 (ОПРЕДЕЛЕНИЕ ПРОИЗВОДНОЙ ФУНКЦИИ В ТОЧКЕ И ЕЁ ОСНОВНЫЕ СВОЙСТВА)

Произво́дная (функции в точке) — основное понятие , характеризующее скорость изменения функции (в данной точке). Определяется как предел отношения приращенияфункции к приращению её аргумента при стремлении приращения аргумента к нулю, если такой предел существует.

БИЛЕТ №15 (ВЫВОД ФОРМУЛЫ ПРОИЗВОДНОЙ СЛОЖНОЙ ФУНКЦИИ)

БИЛЕТ №16 (ВЫВОД ФОРМУЛЫ ПРОИЗВОДНОЙ ОБРАТНОЙ И ПАРАМЕТРИЧЕСКИ ЗАДАННЫХ ФУНКЦИЙ.

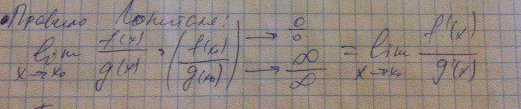ВОПРОС 17. Логарифмическое дифференцирование два способа ВОПРОС 18. ДИФФЕРЕНЦИАЛЬНЫЕ ТЕОРЕМЫ О СРЕДНЕМ ВОПРОС 19. ПРАВИЛО ЛОПИТАЛЯ ДЛЯ РАСКРЫТИЯ НЕОПРЕДЕЛЕННОСТЕЙ ВОПРОС 20. ФИЗИЧЕСКИЙ И ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ K=f`(x0)=tg альфа

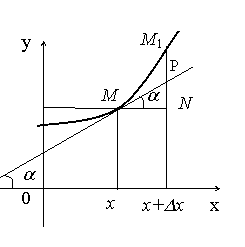
ВОПРОС 21.ОПРЕДЕЛЕНИЕ ДИФФЕРЕНЦИАЛА ФУНКЦИИ , ЕГО ОСНОВНЫЕ СВОЙСТВА

Дифференциал функции – линейная часть приращенной функции

ВОПРОС 22. ДИФФЕРЕНЦИАЛ АРГУМЕНТА. ИНВАРИАНТНОСТЬ ДИФФЕРЕНЦИАЛА И ЕГО ГЕОМЕТРИЧЕСКЙ СМЫСЛ Дифференциал функции y = f(x) равен произведению её производной на приращение независимой переменной x (аргумента). Вопрос 23. Определение асимптот. Их классификация. Связь асимптот с областью определения функции. Вывод предельных соотношений для нахождения асимптот. 1.Асимптота - прямая, обладающая тем свойством, что расстояние от точки кривой до этой прямой стремится к нулю при удалении точки вдоль ветви в бесконечность. 2.Классификация - вертикальная , горизонтальная ,наклонная 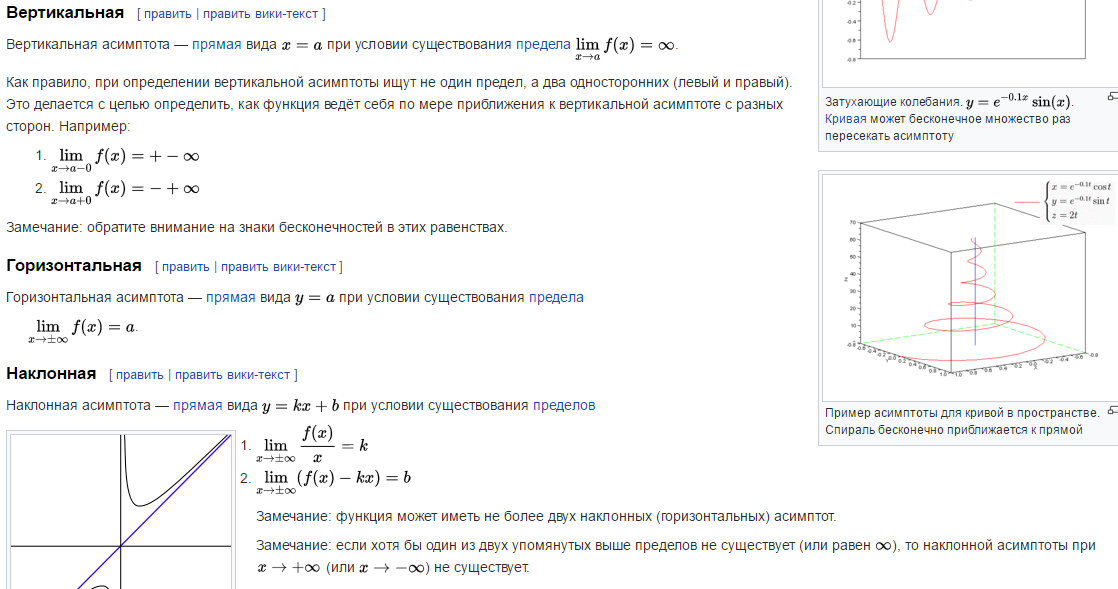3.СВязь асимптот с областью определения функции 4. ХЗ Вопрос 24.Монотонность функции. Признаки монотонности дифференцируемой функции. 1. Если функция возрастает или убывает на некотором промежутке, то она называется монотонной на этом промежутке Функция у=f(x) строго возрастает ,если большему значению аргумента соответствует большее значение функции функция у=f(x) строго убывает если меньшему значению аргумента соотв. меньшее значение функции. 2.Если f^(x) >0 ,то функция возрастает на данном отрезке Меньше нуля ,убывает на данном отрезке Вопрос 25. Определение точек максимума и минимума функции В точке производная меняет свой знак с плюса на минус, т.е. при функция имеет максимум. В точке производная меняет свой знак с минуса на плюс, т.е. при функция имеет минимум. В точке производная своего знака не меняет, т.е. экстремума там нет. Вопрос 26. Необходимое условие и два достаточных условия существования точек экстремума. (Необходимое условие экстремума)

Если функция имеет экстремум в точке , то ее производная либо равна нулю, либо не существует.

(Первое достаточное условие экстремума)

Пусть для функции выполнены следующие условия:

1. функция непрерывна в окрестности точки ;

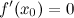2. или 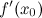не существует;

3. производная 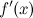при переходе через точку 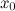меняет свой знак.

Тогда в точке функция имеет экстремум, причем это минимум, если при переходе через точку производная меняет свой знак с минуса на плюс; максимум, если при переходе через точку производная меняет свой знак с плюса на минус.

(Второе достаточное условие экстремума)

Пусть для функции выполнены следующие условия:

1. она непрерывна в окрестности точки ;

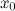2. первая производная в точке ;

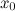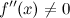3. в точке .

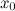Тогда в точке достигается экстремум, причем, если , то в точке функция имеет минимум; если , то в точке функция достигает максимум.

вопрос 27. наибольшее и наименьшее значения функции на отрезке. теорема вейерштрасса. 1.Наибольшим значением функции y=f(x) на промежутке X называют такое значение , что для любого справедливо неравенство .

Наименьшим значением функции y=f(x) на промежутке X называют такое значение , что для любого справедливо неравенство .

2.Теорема Вейерштрасса об ограниченной сверху возрастающей последовательности (или ограниченной снизу убывающей последовательности) утверждает, что любая ограниченная сверху монотонно возрастающая (или ограниченная снизу монотонно убывающая) последовательность имеет предел, причем этот предел равен её точной верхней (или нижней) грани.

ВОПРОС 28.ВЫПУКЛОСТЬ КРИВЫХ, ТОЧКА ПЕРЕГИБА И 2 ПРОИЗВОДНАЯ. 1)выпуклая кривая - кривая которая лежит по одну сторону от любой касательной прямой 2.Точки кривой, которые разделяют ее выпуклые и вогнутые участки, называются точками перегиба кривой. 3.вторая производная - производная от первой производной ВОПРОС 29. АЛГОРИТМ ИССЛЕДОВАНИЯ ФУНКЦИИ 1. область определения D(у) , непрерывность , четность/нечетность , периодичность 2.асимптоты 3.монотонность и экстремумы 4.точки пересечения графика с осями 5.график ВОПРОС 30. ОПРЕДЕЛЕНИЕ НЕОПРЕДЕЛЕННОГО ИНТЕГРАЛА. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ 1. Неопределенный интеграл - множество первообразных функций f(x) 2. интеграл f(x) dx = F(x)+C(Первое достаточное условие экстремума)

Пусть для функции выполнены следующие условия:

1. функция непрерывна в окрестности точки ;

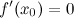2. или не существует;

3. производная 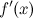при переходе через точку 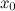меняет свой знак.

Тогда в точке функция имеет экстремум, причем это минимум, если при переходе через точку производная меняет свой знак с минуса на плюс; максимум, если при переходе через точку производная меняет свой знак с плюса на минус.

(Второе достаточное условие экстремума)

Пусть для функции выполнены следующие условия:

1. она непрерывна в окрестности точки ;

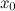2. первая производная 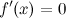в точке ;

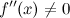3. в точке .

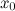Тогда в точке достигается экстремум, причем, если , то в точке функция имеет минимум; если , то в точке функция достигает максимум.

ВОПРОС 28.ВЫПУКЛОСТЬ КРИВЫХ, ТОЧКА ПЕРЕГИБА И 2 ПРОИЗВОДНАЯ. 1)выпуклая кривая - кривая которая лежит по одну сторону от любой касательной прямой f(x)dx - подынтегральное выражение F(x) - подынтегральная функция

dx - дифференциал х С - произвольная постоянная ВОПРОС 31. СВОЙСТВА НЕОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ. ПРОСТЕЙШИЕ СПОСОБЫ ИНТЕГРИРОВАНИЯ; МЕТОД РАЗЛОЖЕНИЯ И ПОДСТАНОВКИ. 1. интеграл (f(x)dx)` = (F(x)+C)`=f(x) 2. интеграл (d (F(x))= интеграл F`(x) dx= интеграл f(x)dx=F(x)+C 3, интеграл k* f(x)dx=k интеграл  f(x) dx 4. интеграл f(x) +- g(x) = интеграл f(x) dx +- интеграл g(x) dx Метод разложения - Задача нахождения неопределенных интегралов от многих функций решается методом сведения их к одному из табличных интегралов. Метод интегрирования подстановкой заключается во введении новой переменной интегрирования ln x * 1/x dx= интеграл t/ln x * t/ dlnx = интеграл t dt = t^2 / 2 +С = ln ^2 *x/2+C ВОПРОС 32.ВЫВОД ФОРМУЛЫ ИНТЕГРИРОВАНИЯ ПО ЧАСТЯМ (u(x) * V(x)` =u`(x) * V(x)+ u(x)*V`(x) ВОПРОС 33. РЕКУРСИВНОЕ ИНТЕГРИРОВАНИЕ И РЕКУРРЕНТНЫЕ ФОРМУЛЫ интеграл n = S=an реккурентные формулы a n=a n-1 + d b n=q* и b n-1 вопрос 34. дробно-рациональные функции и их классификация

1 Дробно рациональная функция называется отношением двух многочленов     , коэффициенты при степенях x -действительные числа 2.Классфикация

Выделяют два типа простейших дробей :

1) A = const;

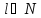
2)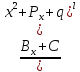 B,C = const ;

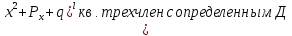
вопрос 35. разложение правильных дробей на простейшие методом неопределенных коэффициентов  

Любую правильную дробь можно разложить на сумму простейших и это разложение будет единственным.

Метод неопределенных коэффициентов:

1. Выписываем подынтегральную функцию

2. Знаменатель раскладываем на множители

3. Представляем эту дробь в виде суммы простых дробей в числителе с коэффициентами А,В,С и т.д. смотря сколько простых дробей

4. Приводим эти дроби к одному знаменателю

5. Приравниваем получившуюся дробь с изначальной

   

6. Дроби равны числители равны

7. Находим коэффициенты А,В,С

8. Записываем ответ

Пример:

36 Разложение неправильной дроби на сумму целой функции и правильной дроби

Разложение по правилу деления. Разделить числитель на знаменатель\

Искомый многочлен-результат деления

Остаток-числитель

Делитель-знаменатель

37 Интегрирование простейших дробей. Интегрирование

правильных дробей

Интегрирование простейших дробей первого типа

Пример :

Интегрирование простейших дробей второго типа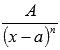 

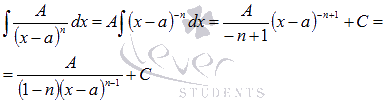
Пример :

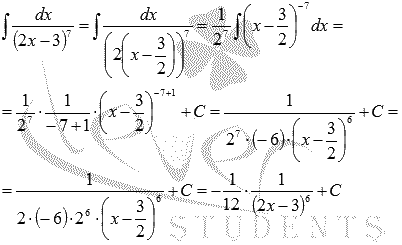
Интегрирование правильных дробей

Рациональная дробь называется правильной, если степень многочлена числителя меньше степени многочлена знаменателя, т.е. . Если же , то дробь называется неправильной.

38 Интегрирование тригонометрических функций с помощью основных тригонометрических формул

39 Универсальная тригонометрическая подстановка

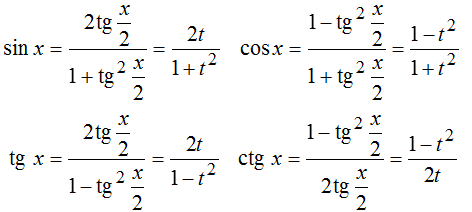
40 Интегрирование простейших иррациональных функций

41 Определение определенного интеграла. Условия интегрируемости .

Необходимое условие интегрируемости

Теорема 1. Если функция f(x) интегрируема на отрезке [a, b], то она ограничена на этом отрезке.

Замечание: Ограниченность функции не является достаточным условием ее интегрируемости.

Достаточные условия интегрируемости

Теорема 2. Если выполнено одно из следующих условий :

функция f(x) непрерывна на отрезке [a, b ];

функция f(x) ограничена на отрезке [a, b] и имеет на этом отрезке конечное число точек разрыва;

функция f(x) монотонна на отрезке [a, b],

то f(x) интегрируема на отрезке [a, b] и, следовательно,

b ∫ a f(x) dx

существует.

42 Свойства определённого интеграла.

1)Однородности

2)Аддитивной по подынтегральной функции

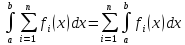
3)Аддитивность пр областям интегрирования

43 Вычисление определенного интеграла. Формула Ньютона-Лейбинца. Формула интегрирования по частям.

Формула Ньютона-Лейбинца

формула интегрирования по частям

44 Интеграл от четной или не четной функции по симметричной области интегрирования

45 Приложение определенного интеграла для вычисления площади плоских фигур

46 Приложение определенного интеграла для вычисления длины плоской дуги

47 Приложение определенного интеграла для вычисления объем тела вращения