
Элтех / Лабы / katya / Вариант 2 / Вар-2 Кадыров Руслан / Лабораторные работы / Лабораторная работа 2 / Лабораторная работа 2
.docxМИНОБРНАУКИ РОССИИ
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
«Национальный исследовательский университет «МИЭТ»
Кафедра: Электротехника.
Дисциплина: Электротехника и электроника. Общая электротехника.
Пояснительная записка к
лабораторной работе №2
на тему:
ИССЛЕДОВАНИЕ ЭЛЕКТРИЧЕСКОЙ ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА
Руководитель:
Гордиевич Л. А.
Выполнил:
ст. гр. МП-23 Кадыров Р. Л.
МИЭТ 2013
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
Синусоидальный (гармонический) ток – периодический переменный ток, при котором мгновенные значения тока и напряжения изменяются по закону синуса (косинуса):

Рис. 1 Некоторый параметр изменяется по закону косинуса. Ось абсцисс – время либо текущая фаза, ось ординат – величина параметра. Высота пика – амплитуда его изменения, расстояние между двумя соседними пиками – период.
Напряжение - u(t) = Um sin (ωt + φ)
Ток - i(t) = Im sin (ωt + φ), где
Um, Im - амплитудные (пиковые - pk) значения
(ωt + φ) - электрическая фаза
φ - начальная фаза напряжения или тока
ω - угловая частота, ω = 2πf, (рад/сек), f - циклическая частота (Гц)
Т=1/f - период повторения (сек).
Действующие значения напряжения/тока за период Т – такие значения постоянных напряжения/тока, при которых падение мощности в цепи равно падению мощности при данном переменном токе.
I=√(1/T∫Im2sin2(ωt + φ)dt)= Im/√2; U=√(1/T∫Um2sin2(ωt + φ)dt)= Um/√2;
Частотные функции (комплексные выражения) действующих значений напряжения и тока (по формуле Эйлера e(jφ) = cosφ + jsinφ; j=√(-1):
Ū = U e(jφ) = U (cosφ + jsinφ) = (U1 + jU2), U = √ ((U1)2 + (U2)2),
Ī = I e(jφ) = I (cosφ + jsinφ) = (I1 + jI2), U = √ ((I1)2 + (I2)2).
Действующее значение резистивного сопротивления и проводимости: R, g = 1/R. Im=Um/R, I=U/R, i(t)=u(t)/R;
Действующее частотное значение резистивного сопротивления и проводимости: R(ω), G(ω) - const (частотная независимость).
Действующие комплексные значения «R» и «G» сохраняются.
Действующее значение индуктивности – L (катушка индуктивности).
При переменном токе индуктивность обладает некоторым реактивным сопротивлением. Напряжение на ней равно UL=L(di/dt).
Действующее частотное значение индуктивного сопротивления и проводимости: xL = ωL; bL = 1/xL = 1/ωL.
Действующее комплексное значение индуктивного сопротивления и проводимости: XL = jxL = xL e(j90°), BL = –jbL = –j(1/ωL) = bLe(–j90°).
Действующее значение емкости C(конденсатор).
При переменном токе конденсатор также имеет некоторое реактивное сопротивление. Величина напряжения на нем равна UC=1/C∫i(t)dt;
Действующее частотное значение емкостного сопротивления и проводимости: xC = 1/ωC; bC = 1/xC = ωC.
Действующее комплексное значение емкостного сопротивления и проводимости: XC = –jxC = xC e(–j90°), BC = jbC = jωC = bCe(j90°).
Действующее частотное значение полного сопротивления при последовательном соединении R, L, C элементов: z = √(R2 + (xL – xC)2)= √ (R2 + x2).
Im
XL
Z
X Z


φ
X
R
Re 

R Re XC
Рис. 2. Треугольник сопротивлений Рис. 3. Векторы сопротивлений (X=XL-XC)
Полная проводимость при параллельном соединении R, L, C элементов: y = √ (g2 + (bC – bL)2).
Комплексные значения полных сопротивлений и проводимостей: Z = z e(jφ) = R + jx; φ = arctg (x/R) - сдвиг (разность) начальных фаз тока и напряжения Y = y e(jΨ) = g + jb, Ψ = arctg (b/g) = (900 – φ).
Полные комплексные значения мощностей:
Ŝ = Ū×Ï = P ± jQ = S e(jφ). φ = arctg (Q/P) = arctg (x/R) - сдвиг (разность) начальных фаз тока и напряжения источника (ток по R, напряжение по Z).
Действующие значения мощностей.
Полная (смешанная) мощность S = U×I = √ (P2 + Q2), (В*А).
Активная (резистивная) мощность P = S cos φ, P = I2R, (Вт) – мощность, потребляемая нагрузкой.
Реактивная (индуктивно-емкостная) мощность Q = S sin φ, Q = I2x, (В*A) - мощность, забираемая из цепи L и C и впоследствии возвращаемая в неё.
Практическая часть
Вариант 6
Задание 1:
По параметрам варианта рассчитать и записать аналитическое выражение (мгновенное значение) синусоидального сигнала (амплитуду, угловую частоту, период). Собрать схему эксперимента в Multisim, зафиксировать показания вольтметра, осциллографа, частотомера (VRMS, Vpeak, Т,(мс), f(Гц), Ψe(°)).
Дано:
VRMS=2.82 В;
f=150 Гц;
Ψe=150°;
Исходя из этих данных, заполним таблицу:
|
Em , В |
Частота f, Гц f=1/Т |
Период Т, мс Т=1/f |
Угловая частота ω , рад/с ω=2 |
Началь-ная фаза Ψe , °
|
Мгновенное, комплексное значения напряжения |
|||||||
|
Действующие значения (RMS - root-mean-square) VRMS= |
Амплитудные значения, Vpeak=
|
Двойные амплитудные значения, размах (peak to peak) Vp-p, В Vp-p=2Vp |
||||||||||
|
2.82 |
3.988 |
7.976 |
150 |
6 |
942 |
150 |
u=3.988sin(924t+150°) |
|||||
Vpeak=

 VRMS=2.82
VRMS=2.82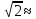 3.988
В;
3.988
В;
Vp-p=2Vpeak=7.976 В;
T=1/f=1/150=0.006 c= 6 мс;
ω=2 f=2
f=2 150=300
150=300
u=Umsin(ωt+ Ψe)= 3.988sin(942t+150°)
По формуле Эйлера,
Ū = Um e(jφ) = U (cosφ + jsinφ)= 3.988ej(924 t+150°) = 3.988 (cos(924 t+150°) + jsin(924 t+150°))

Рис. 1.1. Экспериментальная схема в Multisim.

Рис. 1.2. Показания осциллографа.
Задание 2:
По аналитическому выражению (мгновенное значение) напряжения синусоидального сигнала рассчитать и записать действующее значение, амплитудное значение, полный размах напряжения, частоту, период, начальную фазу. Собрать схему эксперимента в Multisim, снять показания вольтметра, осциллографа и частотомера (VRMS, Vpeak, Т,(мс), f( Гц), Ψe (°)). Изобразить мгновенное(i(t)), комплексное( J ) значения напряжения на временной и векторной диаграммах.
Дано:
u(t)=310sin(314t-240°);
Учитывая, что , u=Umsin(ωt+ Ψe), заполним таблицу:
|
Em , В |
Частота f, Гц f=1/Т |
Период Т, мс Т=1/f |
Угловая частота ω , рад/с ω=2 |
Началь-ная фаза Ψe , °
|
Мгновенное, комплексное значения напряжения |
|||||||
|
Действующие значения (RMS - root-mean-square) VRMS= |
Амплитудные значения, Vpeak=
|
Двойные амплитудные значения, размах (peak to peak) Vp-p, В Vp-p=2Vp |
||||||||||
|
219.9 |
310 |
620 |
50 |
20 |
314 |
-240 |
u=310sin(314t-240°) |
|||||
VRMS=
Vpeak/20.5 ;
;
Vpeak= 310 В;
Vp-p=2Vpeak=620 В;
ω=314
T=2π/ ω =2π/100π=0.02 c= 20 мс;
f=1/T=1/0.02=50 Гц;
Ψe=-240°;
По формуле Эйлера, Ū = Um e(jφ) = U (cosφ + jsinφ)=310ej(314t-240°) = 310 (cos(100πt-240°) + jsin(100πt-240°)) B;
Ī =Ū/R=0.310ej(100πt-240°) = 0.310 (cos(100πt-240°) + jsin(100πt-240°)) A=310 (cos(100πt-240°) + jsin(100πt-240°)) мА;

200
100
i, 100 мA/дел
0
-100
-200
t, 5 мс/дел

Рис. 2.1. Мгновенная сила тока i(t)
Im,
j*mA


i0
ω
Im
=310
Re , mA
Ψe= -240°
Ī0
Рис. 2.2. Комплексная сила тока Ī0 в начальный момент времени.
Ī 0=
0.310ej(-240°)
= 0.310 (cos(-240°) + jsin(-240°)) A=-0.310 (-cos(60°) +
jsin(60°)) A =-0.155(1-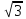 j)
A=-155(1-
j)
A=-155(1- j)
mA;
j)
mA;

Рис. 2.3. Экспериментальная схема в Multisim.

Рис. 2.4. Показания осциллографа.
Задание 3:
R элемент в линейной электрической цепи синусоидального тока. Используя аналитическое выражение источника ЭДС (данные из таблицы 2) собрать принципиальную электрическую схему с R элементом. Рассчитать мгновенное значение тока, напряжения, мощности, действующие комплексные значения тока, напряжения, мощности. Собрать схему эксперимента в Multisim, снять показания осциллографа (VRMS, Vpeak, Т,(мс), f( Гц), Ψe (°), i(t), u(t), p(t)).
Дано:
u(t)=310sin(314t-240°);
R1 = 8 Ом;
R2 = Rвн = 30 мОм = 0,03 Ом;
Исходя из этих данных, заполним таблицу:
|
Em , В |
Частота f, Гц f=1/Т |
Период Т, мс Т=1/f |
Угловая частота ω , рад/с ω=2 |
Началь-ная фаза Ψe , °
|
Мгновенное, комплексное значения напряжения |
|||||||
|
Действующие значения (RMS - root-mean-square) VRMS= |
Амплитудные значения, Vpeak=
|
Двойные амплитудные значения, размах (peak to peak) Vp-p, В Vp-p=2Vp |
||||||||||
|
219.858 |
310 |
620 |
50 |
20 |
100 |
-240° |
u=310sin(100 |
|||||
Vpeak=310 В;
VRMS=Vpeak/20.5=219.858 В;
T=1/f=1/50=0.02 c= 20 мс;
ω=2 f=2
f=2 50=100
50=100
u=Umsin(ωt+
Ψe)=
310sin(100 t-240°);
t-240°);
По формуле Эйлера, Ū = Um e(jφ) = U (cosφ + jsinφ)=310ej(100πt-240°) = 310(cos(100πt-240°) + jsin(100πt-240°))
Ū 0= 310ej(-240°) = 310 (-cos(60°) + jsin(60°)) B
Im,
j*В

Ū0
ω
Ψe=-240°
Um =310 Re , В
Рис. 3.1. Комплексное напряжение Ū0 в начальный момент времени.

Рис. 3.2. Экспериментальная схема в Multisim.

Рис. 3.3. Показания осциллографа.
Мгновенное
значение тока

Для
резистивного сопротивления

Зависимость мощности от времени на резистивном сопротивлении

Задание 4.
L элемент в линейной электрической цепи синусоидального тока. Используя аналитическое выражение источника ЭДС (данные из таблицы 2) собрать принципиальную электрическую схему с L элементом. Рассчитать мгновенное значение тока, напряжения, мощности, действующие комплексные значения тока, напряжения, мощности. Собрать схему эксперимента в Multisim, снять показания осциллографа (VRMS, Vpeak, Т,(мс), f( Гц), Ψe (°), i(t), u(t), p(t)).
VRMS = 219.858 В
Vpeak, =310 В
f = 50 Гц,
Ψe =-240°
Т,(мс) = 20 мс
По
закону Ома находим ток протекающий
через катушку индуктивности


Сопротивление
катушки индуктивности

Ток
протекающий через катушку индуктивности


Соотношение
фазы напряжения и тока на индуктивности


Рис. 4.1. Экспериментальная схема в Multisim.

Рис. 4.2. Показания осциллографа в четвертом эксперименте.
Анализ мгновенной мощности в индуктивном элементе


Из аналитического выражения для мощности можно сделать вывод, что это знакопеременная функция, изменяющаяся с двойной частотой по отношению к частоте изменения напряжения UL и тока IL в цепи. Среднее значение мощности PL(t) за период T равно нулю. В индуктивном элементе в первую четверть периода T напряжение UL и ток IL имеют знак плюс, поэтому мощность больше нуля, т.е. Индуктивный элемент потребляет электрическую энергию источника и преобразовывает её в магнитную, накапливая её в магнитном поле катушке. Во вторую четверть периода напряжение UL и ток IL имеют противоположные знаки, поэтому мощность отрицательна. В это время накопленная магнитная энергия возвращается источнику, преобразовываясь в электрическую энергию. В третьей четверти происходит накопление энергии в магнитном поле элемента L, в четвертой — её возврат источнику энергии.
Задание 5.
C элемент в линейной электрической цепи синусоидального тока. Используя аналитическое выражение источника ЭДС (данные из таблицы 2) собрать принципиальную электрическую схему с C элементом. Рассчитать мгновенное значение тока, напряжения, мощности, действующие комплексные значения тока, напряжения, мощности. Собрать схему эксперимента в Multisim, снять показания осциллографа (VRMS, Vpeak, Т,(мс), f( Гц), Ψe (°), i(t), u(t), p(t)).
VRMS = 219,858 В
Vpeak, =310 В
f = 50 Гц,
Ψe =-240°
Т= 0,02 с
С= 7 нФ
Соотношение
фазы тока и напряжения на конденсаторе

Реактивное
емкостное сопротивление
 Ом
Ом
По
закону Ома
 и
и



Рис. 5.1. Экспериментальная схема в Multisim.

Рис. 5.2. Показания осциллографа.
Анализируя
мгновенную мощность в емкостном элементе


заключаем, что это знакопеременная функция времени, изменяющаяся в противофазе с реактивной индуктивностью мощностью PL
Среднее значение мощности Pc(t) за период рано нулю.
В ёмкостном элементе в первую очередь периода T напряжения Uc и ток Ic имеют разные знаки, это означает, что емкостной элемент в первую четверть возвращает накопленную электростатическую энергию источнику. Во вторую четверть периода ток и напряжение имеют одинаковое направление и следовательно конденсатор заряжается. В третьей четверти происходит вовзрат энергии, в четвертой зарядка конденстора энергией.
Вывод
Мы рассмотрели 3 случая задания значений источника ЭДС: VRMS , Vpeak, Vp-p;
во всех случаях показания вольтметра совпадают с VRMS, то есть оно показывает действующее значение напряжения U. Также мы рассчитали теоретически компоненты уравнения мгновенного напряжения и сверили их с показаниями осциллографа. Они сходятся с достаточно высокой точностью. Мы получили тригонометрические и комплексные уравнения u(t) и i(t) и построили по ним графики.
Мы научились переводить действующие значения Em в амплитудное. Рассмотрели схемы с разными их значениями. Научились строить векторные диаграммы комплексных значений.

 f
f
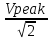

 VRMS
VRMS f
f


 VRMS
VRMS 100
100
 f
f
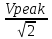
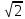
 VRMS
VRMS
 t-240°)
t-240°)