20. Для электрической цепи выполнить расчет схем относительно напряжений ветвей.
Пусть имеем схему по рис. 1, где 
-
источник тока. В соответствии с
рассмотренным нами ранее законом Ома
для участка цепи с ЭДС для данной схемы
можно записать:
|
|
(1) |
.
Однако, для дальнейших выкладок будет
удобнее представить ток 
как
сумму токовk-й
ветви и источника тока, т.е.:
|
|
(2) |
.Подставив (2) в (1), получим:
|
|
(3) |
. Формула (3) представляет собой аналитическое выражение закона Ома для участка цепи с источниками ЭДС и тока (обобщенной ветви).
Соотношение (3) запишем для всех nветвей схемы в виде матричного равенства
или
|
|
(4) |
,где Z– диагональная квадратная (размерностьюn x n) матрица сопротивлений ветвей, все элементы которой (взаимную индуктивность не учитываем), за исключением элементов главной диагонали, равны нулю.
Соотношение (4) представляет собой матричную запись закона Ома.
21. Расчет схем методом узловых потенциалов в топологической форме.
В матричном виде система уравнений для метода узловых потенциалов выглядит следующим образом]:
,
где
—
матрица соединений размера (q – 1)
× p (q — количество узлов, р —
количество рёбер) , в которой i–я
строка соответствует узлу i, а j–й
столбец соответствует ребру j, причём
элемент Aij равен
0, если ребро j не присоединено к узлу i;
1, если ребро выходит из узла;
–1, если ребро входит в узел.
Понятие «входит» и «выходит» означает, что для каждого ребра задаётся направление, которое обычно ассоциируется с направлением тока в этом ребре;
—
диагональная матрица проводимостей
размера p × p, в которой диагональный
элемент Yii равен проводимости i–го
ребра, а недиагональные элементы равны
нулю;
—
транспонированная матрица соединений;
—
матрица-столбец узловых потенциалов
размером (q – 1) × 1. Потенциалы измеряется
относительно предварительно выбранного
узла, потенциал которого считается
равным нулю. Нулевой узел не входит ни
в одну из перечисленных в данном разделе
матриц;
—
матрица-столбец источников тока
размером p × 1, где каждый элемент
равен току соответствующего источника,
причём эта величина нулевая, если в
данном ребре источник тока отсутствует;
положительная, если направление тока
источника совпадает с направлением
тока в ребре; и отрицательная в противном
случае;
—
матрица-столбец источников ЭДС
размером p × 1, где каждый элемент
равен ЭДС соответствующего источника,
причём эта величина нулевая, если в
данном ребре источник ЭДС отсутствует;
положительная, если направление ЭДС
источника совпадает с направлением
тока в ребре; и отрицательная в противном
случае.
Пример системы уравнений
Для схемы матрицы имеют вид:
Перемножаем матрицы в соответствии с матричным уравнением:
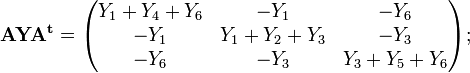
Раскрывая матричную запись, получаем следующую систему уравнений:
22. Переменный синусоидальный ток.
Синусоидальный токпредставляет собой ток, изменяющийся во времени по синусоидальному закону:
Максимальное значение функции называют
амплитудой.Амплитуду тока обозначают
.Период T–
это время, за которое совершается одно
полное колебание.
Частотаравна числу колебаний в 1 с (единица
частотыf- герц (Гц)
или
)
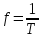
Угловая
частота(единица угловой
частоты – рад/с или
)
Аргумент
синуса, т.е.
,
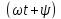называютфазой.
Фаза характеризует состояние колебания
в данный момент времениt.
Любая синусоидально изменяющаяся функция определяется тремя величинами: амплитудой, угловой частотой и начальной фазой.
Под средним значениемсинусоидально изменяющейся величины понимают её среднее значение за полпериода.
Среднее значение тока
т.е. среднее значение синусоидального
тока составляет 2/π=0,638 от амплитудного.
Аналогично,
Действующее значениесинусоидального тока численно равно значению такого постоянного тока, который за время, равное периоду синусоидального тока, выделяет такое же количество теплоты, что и синусоидальный ток.
Действующее значение тока
Аналогично,
Количество теплоты, выделенное за один период синусоидальным током,
Выделенная за то же время постоянным током теплота равна
Приравняем их:
