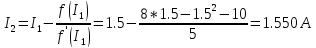- •1.Элементы электрических цепей
- •2.Математические модели элементов электрических цепей
- •3.Двухполюсники резистивного типа
- •4. Двухполюсники индуктивного типа.
- •5. Двухполюсник ёмкостного типа.
- •6.Взаимная индуктивность.
- •7. Законы Кирхгофа и мощности в цепях постоянного тока. Баланс мощности. Законы Кирхгофа
- •Баланс мощностей
- •8. Зависимые источники энергии
- •9. Свойства наложения, взаимности и их применения для анализа электрической цепи. Принцип наложения
- •Свойство взаимности
- •10. Метод эквивалентного генератора.
- •11. Расчёт сложных схем по уравнениям Кирхгофа.
- •12. Метод контурных токов.
- •13. Метод узловых потенциалов
- •16. Для электрической цепи составить матрицу соединений контур-ветвь.
- •17. Для электрической цепи составить матрицу соединений узел-ветвь.
- •18. Для электрической цепи составить матрицу сечений.
- •19. Метод контурных токов в топологической форме. Расчет схем относительно токов хорд.
- •20. Для электрической цепи выполнить расчет схем относительно напряжений ветвей.
- •21. Расчет схем методом узловых потенциалов в топологической форме.
- •22. Переменный синусоидальный ток.
- •23.Изображение сигналов синусоидального тока векторами и комплексными числами.
- •24.Дифференциальные и интегральные зависимости в цепях переменного тока.
- •25 Электрический ток и напряжения на rlc-элементах. Комплексное полное сопротивление.
- •26. Топографические диаграммы токов и напряжений для сложных цепей синусоидального тока.
- •27. Мощности в цепях синусоидального тока.
- •28. Баланс мощностей в цепях синусоидального тока
- •Резонанс напряжений (резонанс в последовательном контуре)
- •Резонанс и частотные свойства.
- •30. Резонанс тока в параллельныхRlc-цепях. Построение ачх токов и фчх
- •31. Периодические несинусоидальные токи, напряжения, эдс.
- •32. Особенности расчета линейных электрических цепей при несинусоидальных сигналах.
- •34. Классический метод расчета переходных процессов с одним накопителем энергии. Включение rl – цепи на постоянном напряжении и ее отключение.
- •35. Классический метод расчета. Включение rc – цепи на постоянное напряжение.
- •36. Классический метод расчета переходных процессов при подключении rl цепи на эдс синусоидального тока.
- •В пределе примаксимальный ток
- •1. Некорректные начальные условия rl-цепи.
- •2. Некорректные начальные условия rc-цепи.
- •38. Включение rlc-цепи на постоянное напряжение. Апериодический характер процесса.
- •39. Включение rlc – цепи на постоянное напряжение. Граничный характер процесса.
- •40. Включение rlc – цепи на постоянное напряжение. Колебательный характер процесса.
- •41. Операторный метод расчета переходных процессов. Свойства преобразования Лапласа.
- •I. Свойство линейности.
- •42. Операторные схемы замещения электрических цепей с одним накопителем и их расчет в изображениях.
- •43. Применение теоремы разложения для нахождения оригиналов по изображениям Лапласса.
- •44.Пассивные четыхполюсники. Прямое и обратное включение. Свойсто взаимности и симметричности.
- •45. Уравнение четырехполюсников в y – параметрах.
- •46. Уравнение четырехполюсников в z – параметрах.
- •47. Уравнение четырехполюсников вА – параметрах.
- •48.Эквивалентные схемы замещения четырехполюсника
- •49. Расчёт а параметров для “т” образной схемы замещения.
- •50. Характеристические параметры четырёхполюсников
- •51.Соединение четырехполюсников. Последовательное соединение.
- •52.Соединение четырехполюсников. Параллельное соединение.
- •53.Каскадное соединение четырехполюсников.
- •54.Свойство регулярности составных четырехполюсников.
- •55.Методы расчёта нелинейных цепей
- •56.Графоаналитический метод расчёт нелинейных цепей
- •57. Расчет схем с нелинейными элементами методом деления отрезков пополам.
- •58. Алгоритм расчета нелинейных цепей по методу Ньютона-Рафсона.
56.Графоаналитический метод расчёт нелинейных цепей

Статическое сопротивление определяется формулой:

Дифференциальное сопротивление

Метод верен, если расчёт производится в рабочей точке А, то есть отклонения токов и напряжения от неё незначительны, тогда на небольших участках ВАХ можно заменить на прямую линию, уравнение которой:


Тогда нелинейный элемент можно заменить эквивалентной схемой элемента:

Если разделим уравнение на rдиф, то получим:
 или
или
Тогда эквивалентная схема будет:

Если ВАХ имеет следующий вид:
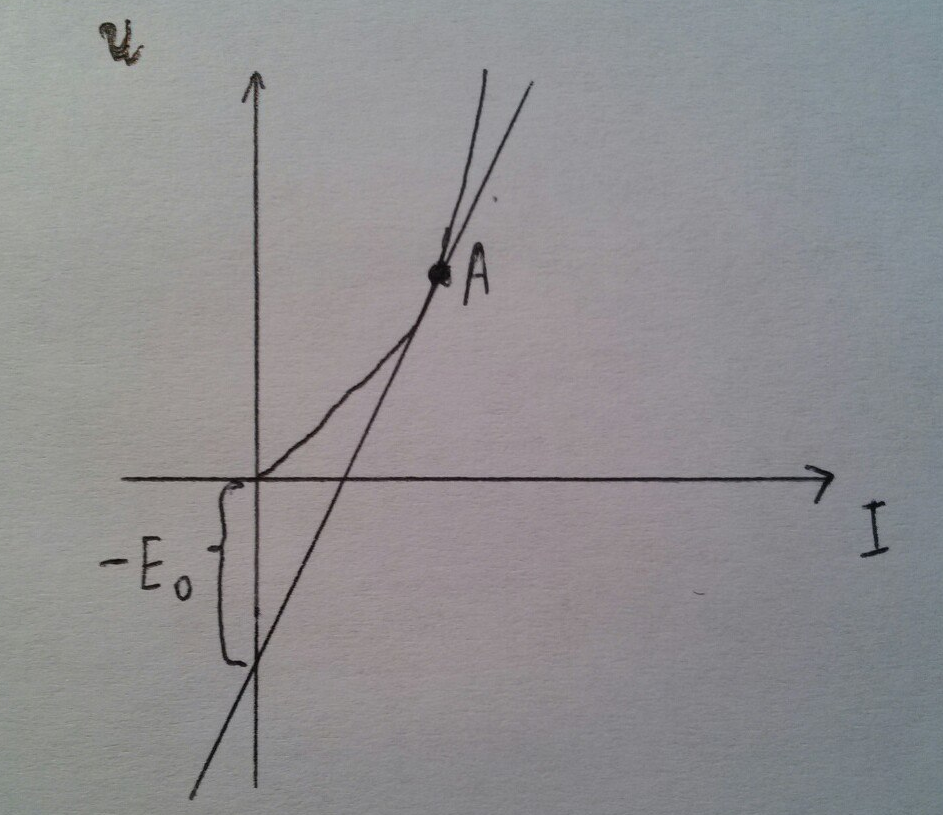
То уравнение будет:

Нелинейный элемент можно заменить эквивалентной схемой элемента:

Если разделим уравнение на rдиф, то получим:

Тогда эквивалентная схема будет:
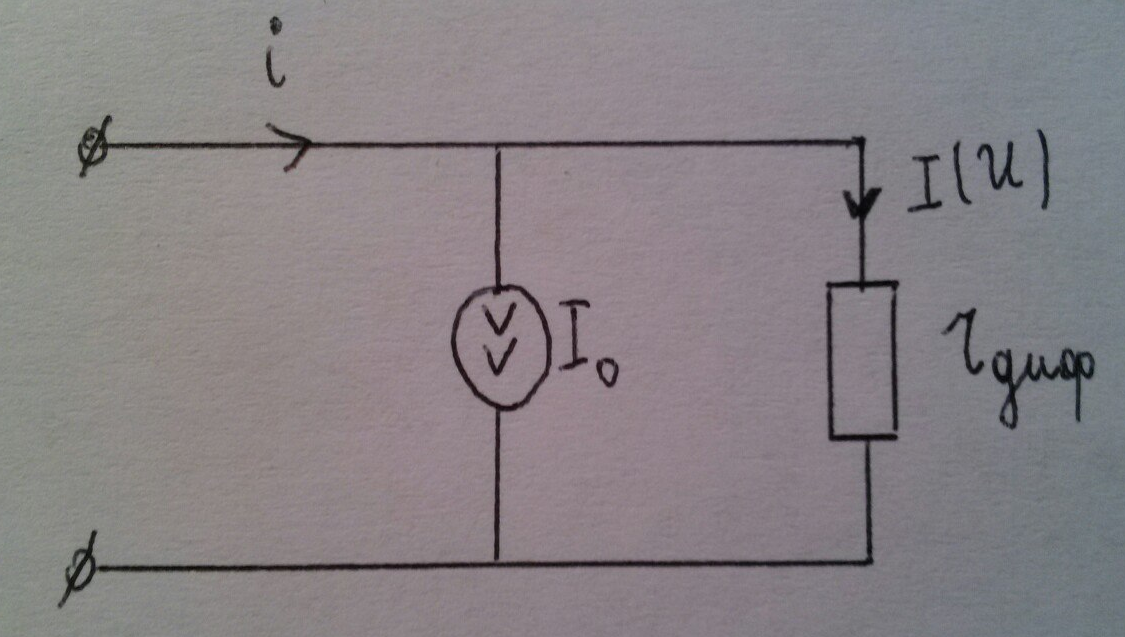
После замены нелинейного элемента эквивалентной схемой проводим расчёт цепи.
57. Расчет схем с нелинейными элементами методом деления отрезков пополам.
Метод деления отрезков пополам используется для определения корней функции одной переменной.
Поделим отрезок [a, b] пополам точкой c, координата которой c = (a + b) / 2 и вычислим значение функции f(c).
Возможны
два случая:
а) f(a)* f(c) >0, т.е. значения функции на концах отрезка [a, c] одинаковы по знаку; тогда корень уравнения находится на отрезке [c, b] и отрезок [a, c] можно исключить из дальнейшего рассмотрения, перенеся точку a в точку c: a=c; f(a)=f(c)

б) f(a)* f(c) <0, т.е. значение функции на концах отрезка [a, c] противоположны по знаку; тогда корень находится на отрезке [a, c] и отрезок [c, b] можно исключить из дальнейшего рассмотрения, перенеся точку b в точку c: b=c
После исключения правой или левой половины отрезка продолжают деление пополам до тех пор, пока длина оставшегося интервала [a, b] не станет меньше некоторой заданной малой величины e, и тогда любое значение аргумента из отрезка [a, b] можно считать корнем с абсолютной погрешностью e. Обычно принимают в качестве корня середину отрезка.
Пример.Найти ток в схеме, если
ВАХ
нелинейного элемента задана уравнением

Решение.

С
учетом того, что








58. Алгоритм расчета нелинейных цепей по методу Ньютона-Рафсона.
Пусть
нелинейное уравнение имеет единственный корень
имеет единственный корень
В
окрестности этого корня функция разлагается
в ряд Тейлора:
разлагается
в ряд Тейлора:

Отсюда
следует:

Где является поправкой к предыдущему
решению.
является поправкой к предыдущему
решению.
Полученное соотношение – алгоритм итерационного метода Ньютона –
Рафсона, который реализуется следующим образом:
1.
Задаем начальное приближенное значение
искомого решения .
.
2.
Определяем поправку .
Для ее вычисления по выражению функции
находим производную.
.
Для ее вычисления по выражению функции
находим производную.
3.
Определяем уточненное значение корня

4.
Повторяем процесс на следующем шаге и
уточняем предыдущее решение до необходимой
точности.
Геометрическая
интерпретация метода приведена на
рисунке. Касательные, проведенные в
точках ,
определяют значение поправки на
соответствующем шаге, так как
,
определяют значение поправки на
соответствующем шаге, так как или
или
Метод
сходится, если начальное приближение
достаточно близко к решению. Однако,
если ,
решение невозможно.
,
решение невозможно.
Исследования
показывают, что сходимость метода
Ньютона – Рафсона зависит от значения
функции ,
ее наклона
,
ее наклона и от кривизны функции
и от кривизны функции .
Если для всех
.
Если для всех выполняется
неравенство
выполняется
неравенство ,
то процесс сходится.
,
то процесс сходится.
Пример.Найти ток в схеме, если
ВАХ
нелинейного элемента задана уравнением

Решение.

С
учетом того, что


 . Ток в нулевом приближении:
. Ток в нулевом приближении:

Уточненное
решение после первого шага:
После
второго шага: