2 семестр МП / Старые материалы - второй поток / Лекции / Лекция 5 Электростатическое поле в диэлектриках

Раздел 6. Электростатическое поле в диэлектрике

(Подробнее - см. книга Берклеевский курс физики. Том 2, Э.ПАРСЕЛ Электричество и магнетизм, Москва, Наука 1975

Есть в библиотеке ШИФР 537(075.8)П-186)

6.1. Микро- и макрополе, созданное поляризованным веществом.

Итак, как следует из всего вышесказанного, атомы и молекулы часто являются поляризуемыми, т.е. обладают электрическими дипольными моментами. Построим из таких частиц столбик (цилиндрик) поляризованного вещества (см. рисунок). Наш цилиндрик мы представим в виде еще более мелких фрагментов вещества, дисков толщиной dz, площадью поперечного сечения . Рассмотрим электрическое поле, которое создается таким фрагментом вещества в точке наблюдения, расположенной вне нашего цилиндрика.

Хотя вещество в целом электронейтрально, каждый объем данного вещества характеризуется вектором - электрическим дипольным моментом единицы объема вещества.

Пусть он один и то же по всему объему вещества. Найдем потенциал, создаваемый в точке наблюдения нашим диском толщиной dz. Потенциал поля точечного диполя с электрическим моментом найдем по формуле, полученной нами ранее:

(см. лекция 2, пример 3 – потенциал поля точечного диполя)

Учтем, что величина является отрицательной. При дальнейшем

суммировании мы будем двигаться от нижнего основания цилиндра к верхнему, а при таком движении будет уменьшаться, значит является отрицательной величиной, тогда можно записать: .

Теперь найдем потенциал, создаваемый в точке наблюдения всем цилиндром:

Условие нормировки в нашем примере .

Обратим внимание на то, что дипольный момент маленького диска мы можем записать двумя способами:

,

запись в левой части уравнения очевидна, а в правой мы представляем наш диск в виде маленькой гантельки, принимая за заряд на торце большого столбца (заряд полюса диполя).

С учетом этого выражения, полученная формула может быть переписана в виде:

Обратим внимание на то, что подобный результат мы уже получали: такое же электрическое поле, как наш столбик поляризованного вещества, создают 2 разноименных точечных заряда величиной , - поверхностная плотность так называемых связанных зарядов, расположенных на торцах фрагмента вещества. Под действием внешнего электрического поля фрагмент вещества, не являющегося проводником, поляризуется и возникает электрический дипольный момент. Тогда на поверхности вещества выступают связанные заряды. Они отличаются от свободных зарядов в проводниках тем, что связные заряды входят в состав молекул, атомов, а не существуют отдельно от них. Сравнивая формулы и , приходим к выводу, что

, .

Построим из столбиков (только что рассмотренных) плоский слой (пластину) однородно поляризованного вещества. Анализируя полученный результат, получим, что всюду вне однородно поляризованной пластины потенциал такой же, как от двух слоев поверхностных зарядов плотностью , .

Таким образом, поля вне поляризованной пластины и двойного слоя совпадают.

Нарисуем вертикальное сечение плоскопараллельной пластины толщиной , обладающей электрическим дипольным моментом - кусок поляризованного вещества, а рядом – двойной электрический слой, состоящий из монослоёв положительного и отрицательного зарядов, заполненный внутри изолятором; в целом данная система электронейтральна.

- поле, созданное связанными зарядами.

Во внешней области поля, создаваемой этими объектами, одинаковы. Поля внутри пластины и внутри двойного слоя, конечно же, разные. При описании поля в веществе на микроуровне следовало бы интересоваться микрополем, т.е. полем внутри и снаружи любой молекулы или атома. Однако наша цель – найти усредненное по всему объёму, содержащему множество атомов или молекул, электрическое макрополе.

, где - макрополе, - микрополе.

Замечание 1

Пусть объём V, в котором производится усреднение, это - объём столбика вещества, о котором шла речь. Найдем модуль среднего значения поля :

Обратим внимание на то, что поле как внутри, так и снаружи от пластины потенциально. А это значит, что величина рассматриваемого линейного интеграла не зависит от того, вычисляем мы его по внутренней траектории, или по внешней. Аналогичное утверждение справедливо и для поля двойного слоя. Поскольку внешние поля двойного слоя и пластины одинаковы, то одинаковы и соответствующие интегралы.

Таким образом, вместо вычисления интеграла внутри пластины достаточно вычислить его внутри двойного слоя:

Итак, электрическое макрополе внутри поляризованного вещества , т.к. вектора и противонаправлены.

ЕЩЕ РАЗ РИСУНКИ ИЗ КНИГИ, КОТОРУЮ НАДО ПОЧИТАТЬ, ЕСЛИ НЕПОНЯТНО

Берклеевский курс физики. Том 2, Э.ПАРСЕЛ Электричество и магнетизм, Москва, Наука 1975

Есть в библиотеке ШИФР 537(075.8)П-186

Подпись к последнему рисунку можно доказать иначе, без всякой математики (см

стр.314-315)

Пункт 6.2. Электрическое поле Е в веществе, поляризованном в результате погружения его во внешнее электростатическое поле.

Мы будем рассматривать вещество, которое само по себе не поляризовано и не обладает дипольным моментом единицы объема. Но если мы поместим это вещество во внешнее по отношение к нему поле, то вещество под влиянием внешнего поля поляризуется, у него возникает дипольный момент единицы объема, возникает дополнительное поле и реальное электрическое поле внутри вещества будет результатом суперпозиции внешнего поля и поля, созданного индуцированными зарядами.

Рассмотрим плоский конденсатор, сначала пустой:

.

Введем в конденсатор пластину из вещества, которое поляризуется под влиянием поля свободных зарядов, расположенных на обкладке конденсатора.

Пусть рассматриваемое вещество таково, что , тогда в силу соотношения , где - макрополе, получим утверждение, что , где - поле связанных зарядов, расположенных на поверхности вещества. Поскольку поле в веществе – сумма полей , то . Для емкости конденсатора теперь справедлива формула:

Еще Фарадей заметил, что введение в конденсатор вещества, не являющегося проводником электричества, увеличивает его емкость.

  Фильм Зависимость емкости от свойств среды

- диэлектрическая проницаемость вещества - показывает во сколько раз напряженность поля в пустом пространстве, больше, чем в среде, заполненным диэлектриком

Обозначим - диэлектрическая восприимчивость вещества, тогда

Если , а значит и , не зависит от , то дипольный момент единицы объема пропорционален , т.е. ,

Такое вещество будем называть диэлектриком. В литературе можно встретить несколько определений понятия «диэлектрик». Наиболее часто употребимое – это вещество, в котором трудно возбудить электрический ток, непроводник. Определение введенное нами не является распространенным в литературе, однако мы будем пользоваться именно им.

Пункт 6.3. Теорема Гаусса для вектора .

Рассмотрим точечный заряд q в безграничном диэлектрике диэлектрической проницаемостью . В соответствие с формулой для точечного источника и определением диэлектрической проницаемости , запишем:

.

Домножим на , получим .

Найдем поток этого вектора.

. Если заряд распределен с некоторой объемной плотностью, то мы можем написать дифференциальный аналог этого выражения:

С учетом того, что создается как свободными, так и связанными зарядами:

, с другой стороны, а т.к.

, приравниваем и правую скобку перенесем в левую часть

или в интегральной форме - связанный заряд, попавший внутрь этой произвольной гауссовой поверхности.

Итак, мы получили выражение, которое мы можем назвать теоремой Гаусса для вектора .

Граничные условия для вектора .

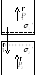
Рассмотрим границу двух диэлектриков (см. рис.)

Рассмотрим верхний диэлектрик и напишем для него теорему Гаусса для вектора :

1) - минус появляется из-за того, что используем не внешнюю, а внутреннюю нормаль. Отсюда получается, что .

2) - так как поток вектора через нашу поверхность отрицательный, то в правой части получается минус. Отсюда

.

Если сблизить диэлектрики, то можно сделать так:

- то есть, на границе диэлектриков происходит скачок вектора .

Если выбрать общую гауссову поверхность, то .

Будем считать, что , тогда - положительное число. Если , тогда , если среда 2 –вакуум, то

Замечание из Иродова (3.6) и (3.13) – это и

П. 6.4. Вектор и теорема Гаусса для вектора.

Как мы знаем , применим тот факт, что . Тогда

. Преобразуем:

- объемная плотность свободных зарядов.

Введем вспомогательный вектор .

или интегральный аналог - - поток вектора через произвольную поверхность равен свободному заряду, попавшему внутрь этой поверхности.

Из последних двух уравнений не следует делать вывод о том, что распределение свободных зарядов является источником поля . В отличие от поля , для равенство циркуляции вектора нулю не работает:

. Поэтому для решения практических задач обратим внимание на следующие граничные условия:

Напишем условие :

, отсюда следует - то есть касательная к границе составляющая поля сохраняется при переходе через границе.

Рассмотрим теперь граничное условие для вектора .

Из того, что следует:

, тогда если на границе раздела диэлектриков нет свободных зарядов, то . Так как

Размерность [Кл/м²]

Замечание 2

В заключении посмотрим одну демонстрацию в кино и одну «живьем»

  Поляризация диэлектрика (разборная лейденская банка)

Демонстрация предназначена для показа явления поляризации диэлектрика и того, что энергия заряженного конденсатора локализована в объеме поляризованного диэлектрика, а не на его обкладках

Диэлектрический эллипсоид во внешнем электрическом поле (см. Гайдуков Г.Н.)

12