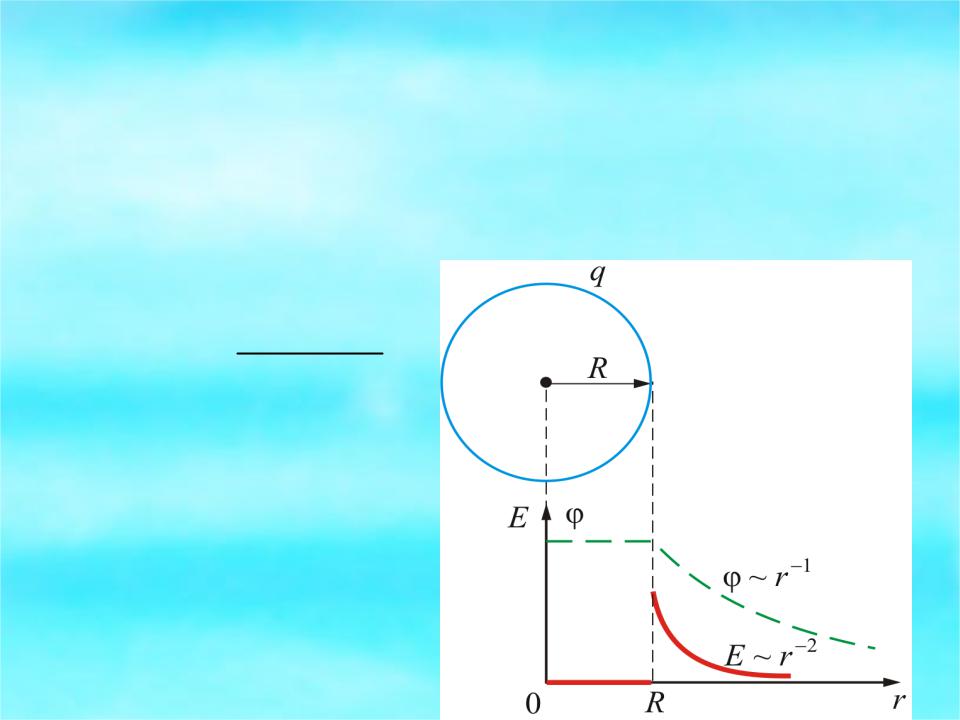
2.7.4. Разность потенциалов заряженной сферы (пустотелой)
Напряженность поля сферы определяется формулой
E(r) q 2
4πε0r
12
А т.к. |
dφ Edr , то |
|
|
|
r2 |
q dr |
|
q |
|
|
1 r2 |
|
q |
|
1 |
|
1 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||||||||
1 |
|
4 |
|
r |
|
4 |
|
|
r |
|
4 |
|
r |
|
r |
|
|||||||
|
|
|
r |
0 |
|
|
0 |
|
r1 |
|
0 |
|
|
|
|||||||||
т.е. |
1 |
q |
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
||||||||
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
4 0r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
13
|
q |
|
σR |
const внутри и на поверхн. |
||
|
|
|
|
|||
4πε0R |
ε0 |
|||||
|
|
|||||
|
|
|
||||
φ |
q |
|
|
|
||
|
вне сферы (r R). |
|||||
|
|
|||||
|
4πε0r |
|
|
|
||
|
|
|
|
|||
14
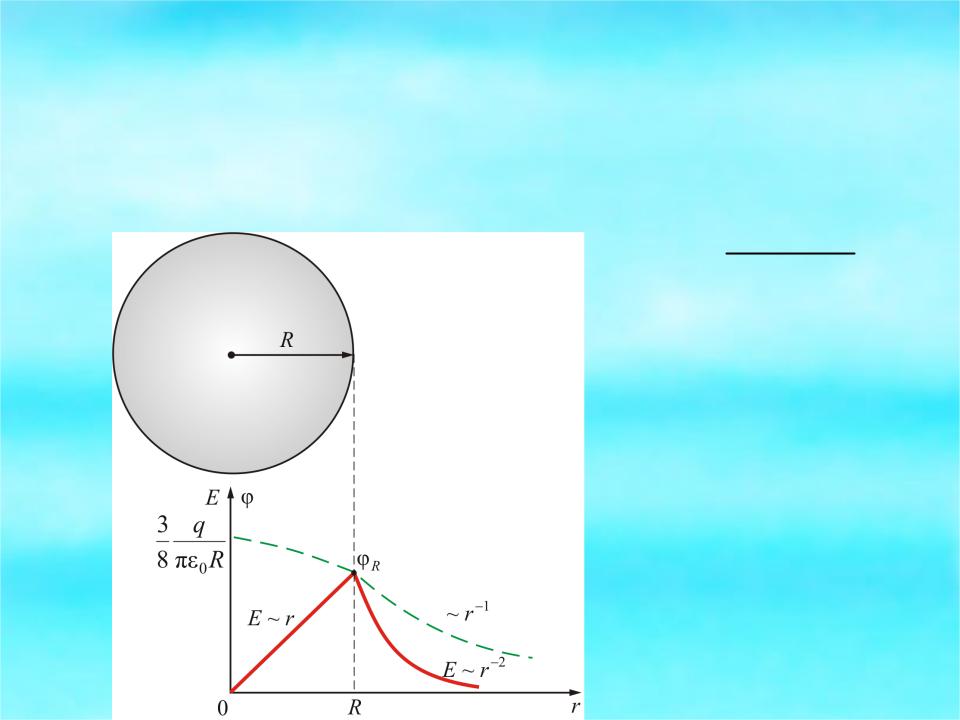
2.7.5. Разность потенциалов внутри диэлектрического заряженного шара
Имеем диэлектрический шар заряженный
с объемной плотностью 3q
ρ 4πR3 .
15
Напряженность поля шара, вычисленная с помощью теоремы Остроградского- Гаусса:
|
|
qr |
|
|
|
|
ρr |
внутри шара(r R) |
|
|
|
|
|
||||
|
|
3 |
|
|||||
|
|
4πε0 R |
|
|
|
|
3ε0 |
|
|
|
q |
|
|
|
на поверхности шара(r R) |
||
E |
4πε0 R2 |
|
||||||
|
|
|
|
|
|
|||
|
|
q |
|
|
|
вне шара (r R). |
||
|
|
|
|
|
|
|||
|
4πε0r2 |
|
||||||
|
|
|
|
|
|
|||
16
Отсюда найдем разность потенциалов шара:
|
|
|
2 |
|
|
|
|
ρ |
|
2 |
|
|
ρ |
r22 r12 |
φ2 |
φ1 |
Edr |
|
|
|
rdr |
|
|||||||
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
3ε |
0 |
|
6ε0 |
|||
|
|
|
1 |
|
|
|
|
1 |
|
|||||
|
|
|
|
|
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q(r 2 |
r 2 ) |
|
|
|||||
|
|
|
|
|
|
|
|
|||||||
|
φ |
|
φ |
2 |
|
|
|
|
2 |
1 |
|
. |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
1 |
|
|
|
4πε0 2R3 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|||||
17
|
Потенциал шара: |
||||||||
3q |
|
вцентре шара (r 0) |
|||||||
|
|
|
|||||||
8πε0 R |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
q |
|
|
r |
2 |
|
|||
φ |
|
3 |
|
|
|
||||
|
|
|
|
2 |
|||||
8πε0 R |
|
R |
внутри шара (r R) |
||||||
|
|
|
|
|
|||||
|
q |
|
на поверхности и вне шара(r R |
||||||
|
|
|
|||||||
4πε0r |
|||||||||
|
|
|
|
|
|
|
|||
18
Из полученных соотношений можно сделать следующие выводы:
С помощью теоремы Гаусса сравнительно просто можно рассчитать Е и φ от различных заряженных поверхностей.
Напряженность поля в вакууме изменяется скачком при переходе через заряженную поверхность.
Потенциал поля – всегда непрерывная
функция координат. |
19 |
|