Кафедра физики
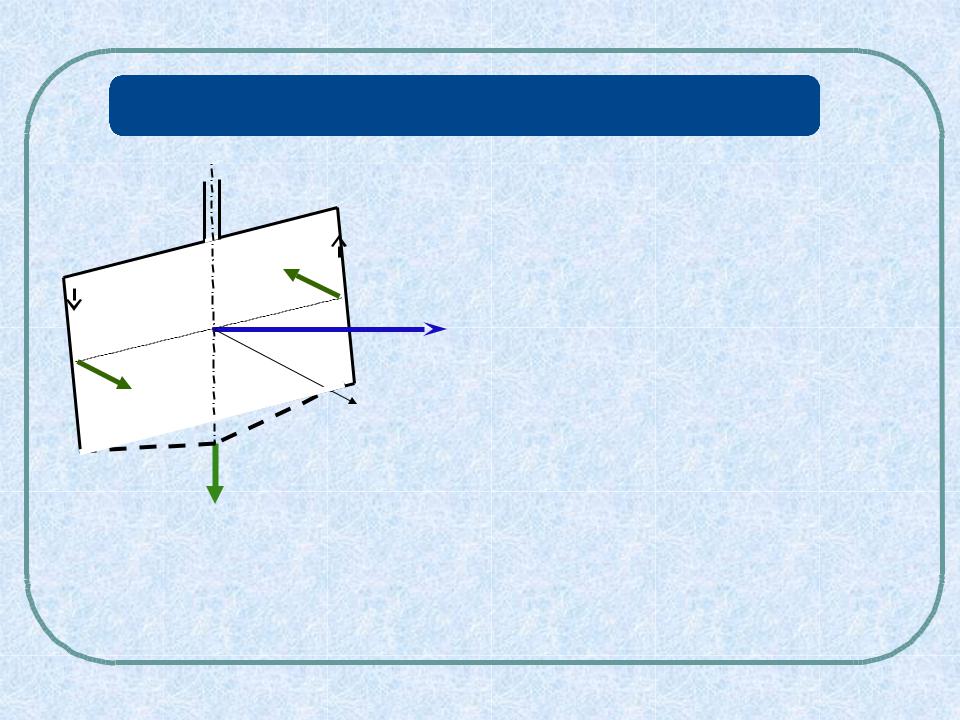
КОНТУР С ТОКОМ В МАГНИТНОМ ПОЛЕ
|
|
a |
|
F |
I |
|
|
|
|
||
I |
|
|
|
b |
|
|
|
|
|
||
b |
F |
|
a |
|
n |
|
|
|
|||
|
|
|
|
|
Силы Ампера, действующие на
стороны a контура, направлены в противоположные стороны вдоль оси контура.
BДействие этих сил сводится только к деформации контура (в зависимости от направления к сжатию или растяжению контура).
Силы Ампера , действующие на стороны контура, плоскости, в которой лежат векторы dlи B. Их направление показано на рисунке.
Кафедра физики
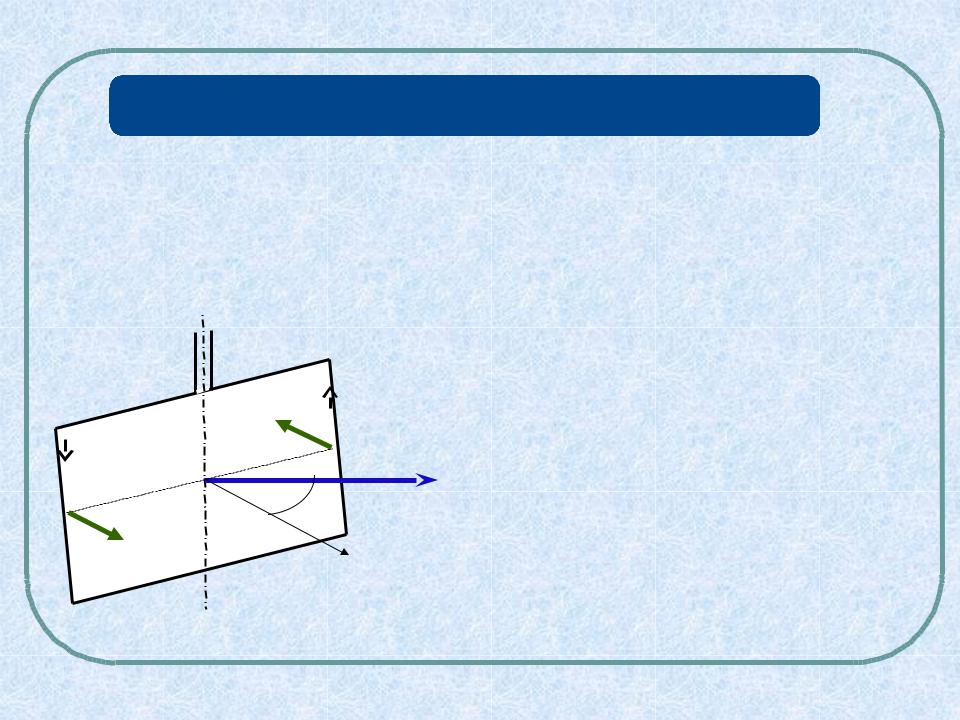
КОНТУР С ТОКОМ В МАГНИТНОМ ПОЛЕ
Численное значение этих сил Ампера определяется выражением
|
F IbB |
|
|
|
|
|
|
Из рисунка видно, что силы, действующие на стороны .b контура, |
|||||||
создают вращающий момент |
M, модуль которого равен |
|
|||||
|
|
|
|
M Fa sin |
|
|
|
|
a |
I |
- угол между нормалью к контуру и |
||||
|
F |
направлением |
|
силовых |
линий |
||
|
|
|
|||||
I |
|
b |
магнитного поля, |
a sin - плечо силы. |
|||
|
B |
|
|
|
|
||
|
|
Подставив выражение для |
|||||
|
|
|
|||||
b |
F |
n |
|
силы |
F |
IbB , получим |
|
a |
M IBab sin |
|
|||||
|
|
|
|||||
|
|
|
|
||||
Кафедра физики
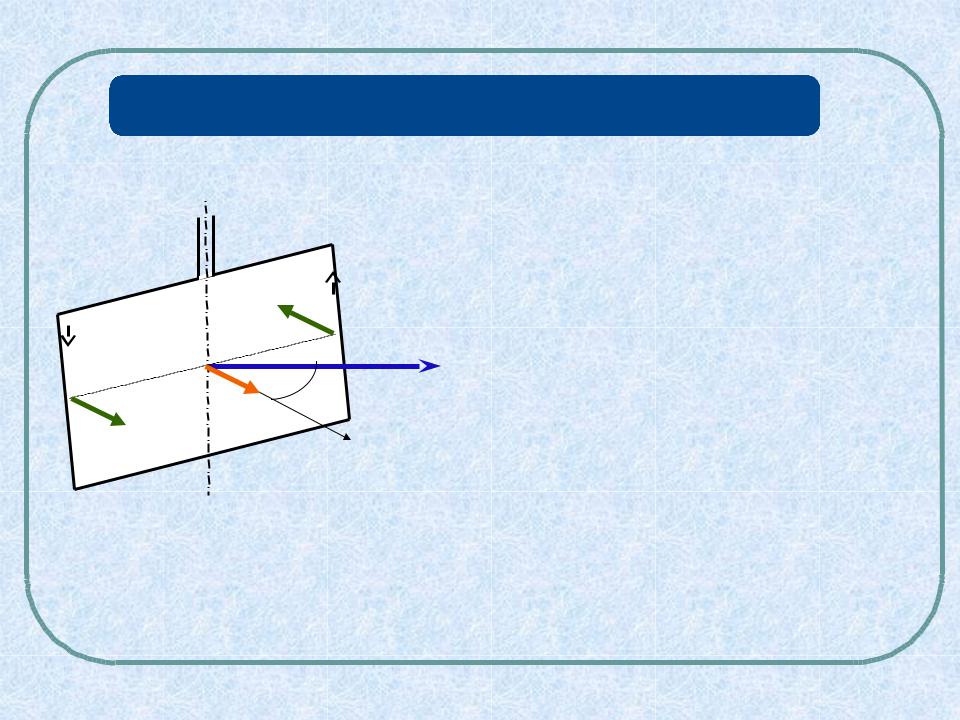
КОНТУР С ТОКОМ В МАГНИТНОМ ПОЛЕ
|
M IBab sin |
ab |
- это площадь, ограниченная контуром, |
||
|
|
|
а |
Iab pm - модуль магнитного момента |
|
|
|
a |
контура с током |
||
|
|
I |
В итоге получим выражение вида |
||
I |
|
F |
b |
M pm B sin |
|
|
|
||||
|
|
pm |
|
B |
|
b |
F |
|
Магнитный момент pm контура с |
||
a |
n |
током по направлению совпадает с |
|||
|
|||||
|
|
|
положительной нормалью контура |
||
Iabn pm
Выражение для вращающего момента можно записать в векторной форме
M pm ,B
Кафедра физики
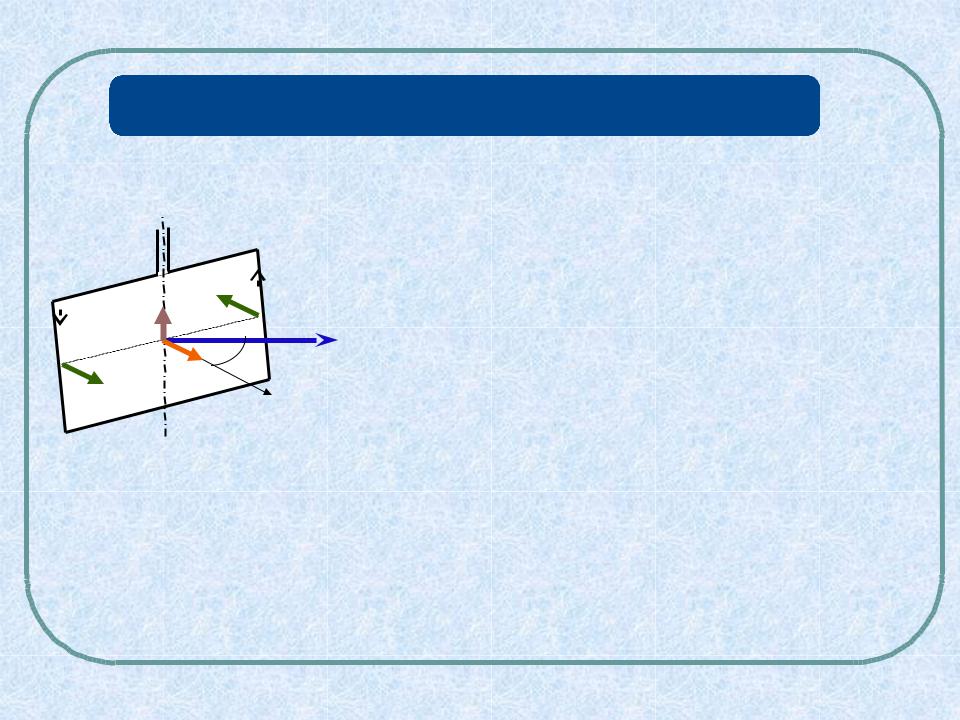
КОНТУР С ТОКОМ В МАГНИТНОМ ПОЛЕ
|
M pm ,B |
|
Теперь легко определить направление |
||||||
|
|
|
|
|
вектора |
M, вспомнив правило: |
|
||
|
|
a |
|
|
векторы |
pm , B и M образуют |
|
||
|
|
F |
I |
правовинтовую ортогональную |
|
||||
|
|
|
|
||||||
I |
|
M |
b |
тройку векторов |
|
|
|||
|
|
B |
Вращающий момент направлен |
||||||
|
|
|
|
||||||
|
F |
|
|
|
по оси вращения контура, |
|
|||
b |
|
pm |
n |
|
. |
плоскости, |
в которой |
||
|
|
a |
|
размещаются |
векторы |
||||
|
|
|
|
|
магнитного |
момента |
и |
||
|
|
|
|
|
|
магнитной индукции |
|
||
Вращающий момент, действующий в однородном магнитном поле на контур с током, стремится сориентировать его перпендикулярно к силовым линиям магнитного поля.
Кафедра физики
КОНТУР С ТОКОМ В МАГНИТНОМ ПОЛЕ
|
M pm ,B |
|
|
Эта формула применима к плоскому |
||
|
|
|
|
|
|
витку произвольной формы |
|
|
a |
F |
I |
|
Кроме того, она может использоваться |
|
|
|
|
|||
I |
|
M |
b |
|
для расчета вращающего момента |
|
|
|
B |
контура в неоднородном магнитном |
|||
|
|
|
||||
|
|
|
|
|
поле. |
|
|
F |
|
pm |
|
|
|
b |
|
n |
|
|
||
|
a |
В неоднородном магнитном поле кроме |
||||
|
|
|||||
|
|
|
|
|||
|
|
|
|
|
вращающего момента, стремящегося повернуть |
|
рамку, будет действовать сила, вызывающая поступательное перемещение рамки с током.
В зависимости от ориентации магнитного момента по отношению к направлению силовых линий магнитного поля контур будет выталкиваться в область более сильного либо более слабого поля
Кафедра физики
ЭФФЕКТ ХОЛЛА - СРС!!! Лабораторная работа в СЛЕДУЮЩЕМ СЕМЕСТРЕ!!!
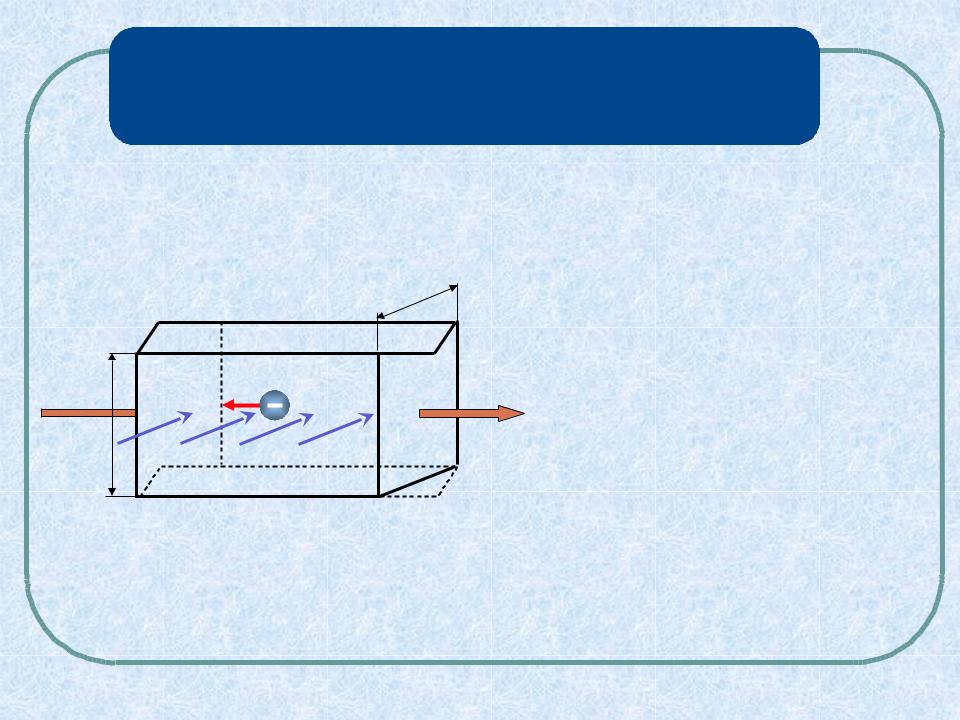
Если металлическую пластинку, вдоль которой течет постоянный электрический ток, поместить в перпендикулярное к ней магнитное поле, то между гранями, параллельными направлениям тока и поля, возникает разность потенциалов. Это эффект Холла
d
|
|
|
|
Поместим |
металлическую |
||
|
|
|
|
пластинку |
с |
плотностью |
|
|
|
v |
|
тока j в магнитное поле B, |
|||
|
|
j |
перпендикулярное j . |
||||
a |
|
|
|||||
|
|
В |
металле |
носителями |
|||
B |
|
|
|||||
|
|
|
|
тока являются свободные |
|||
|
|
|
|
электроны |
|
|
|
Их скорость v направлена против вектора j.
Электроны испытывают действие силы Лоренца
Кафедра физики
|
|
|
ЭФФЕКТ ХОЛЛА |
|
|
|
|
|
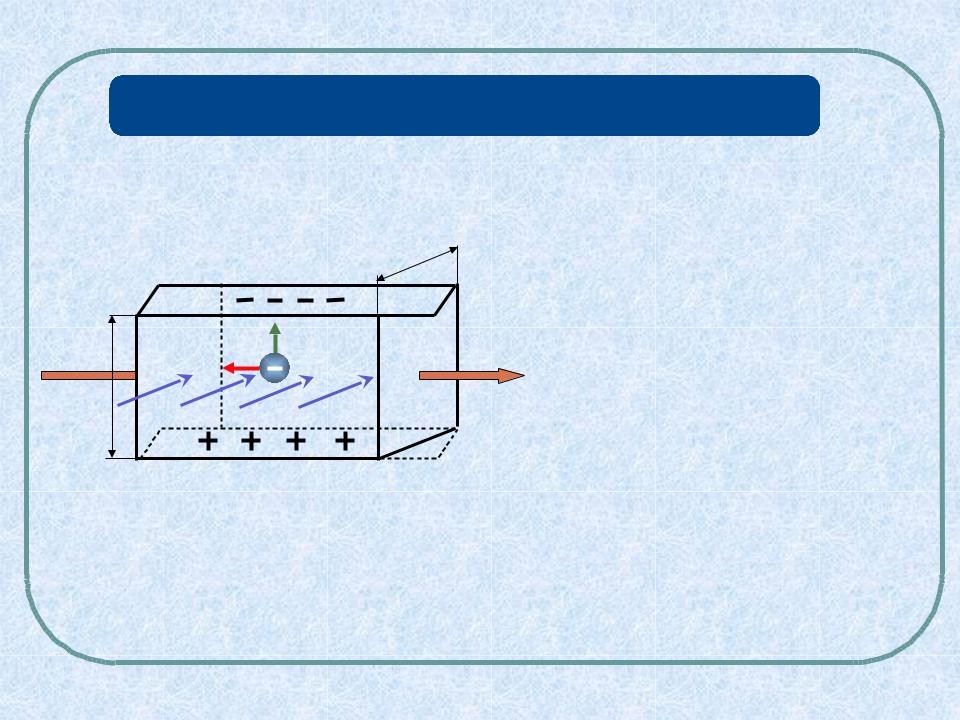
Сила Лоренца направлена вверх (направление определяется |
||||||||
векторным произведением v ,B , с учетом того, что ток переносится |
||||||||
электронами) |
|
d |
В |
результате |
действия силы |
|||
|
|
|
|
Лоренца |
у |
|
электронов |
|
|
|
F |
|
появится |
|
составляющая |
||
|
v |
j |
скорости, направленная вверх |
|||||
|
|
|
|
|
|
|
||
a |
B |
|
У |
верхней |
грани |
|||
|
|
|
пластины |
|
|
образуется |
||
|
|
|
|
избыток |
отрицательных, |
|||
|
|
|
|
у |
нижней |
– |
избыток |
|
|
|
|
|
положительных зарядов. |
||||
В результате возникает поперечное электрическое поле
|
v |
F |
|
|
|
a |
B |
|
|
|
Кафедра физики
ЭФФЕКТ ХОЛЛА
d
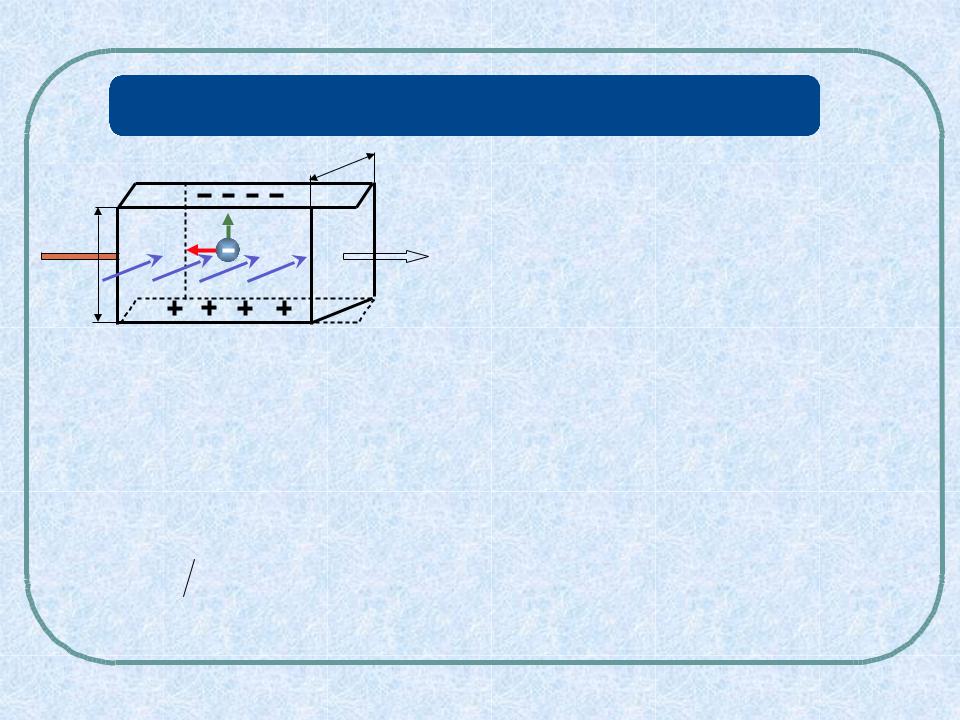
Стационарное распределение зарядов в поперечном 
j направлении установится при таком значении напряженности
электрического поля E , что его действие на заряды будет уравновешивать силу Лоренца.
Возникшую при этом поперечную холловскую разность потенциалов. можно вычислить из условия установившегося стационарного распределения зарядов:
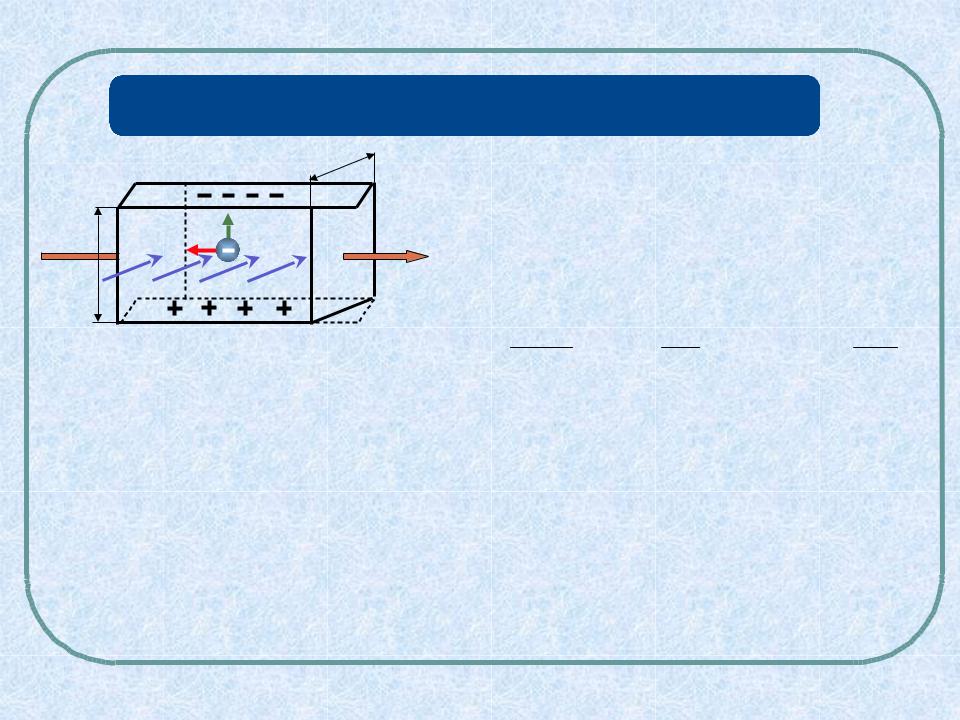
eE e a evB, отсюда |
vBa, a - высота пластинки |
Кафедра физики
ЭФФЕКТ ХОЛЛА
d |
vBa |
|
|
v |
F |
|
|
|
a |
B |
|
|
|
j Учитывая, что сила тока в пластинке I jS envS, получим:
I 1IB1
Ba enSade
S ad - площадь поперечного сечения пластинки
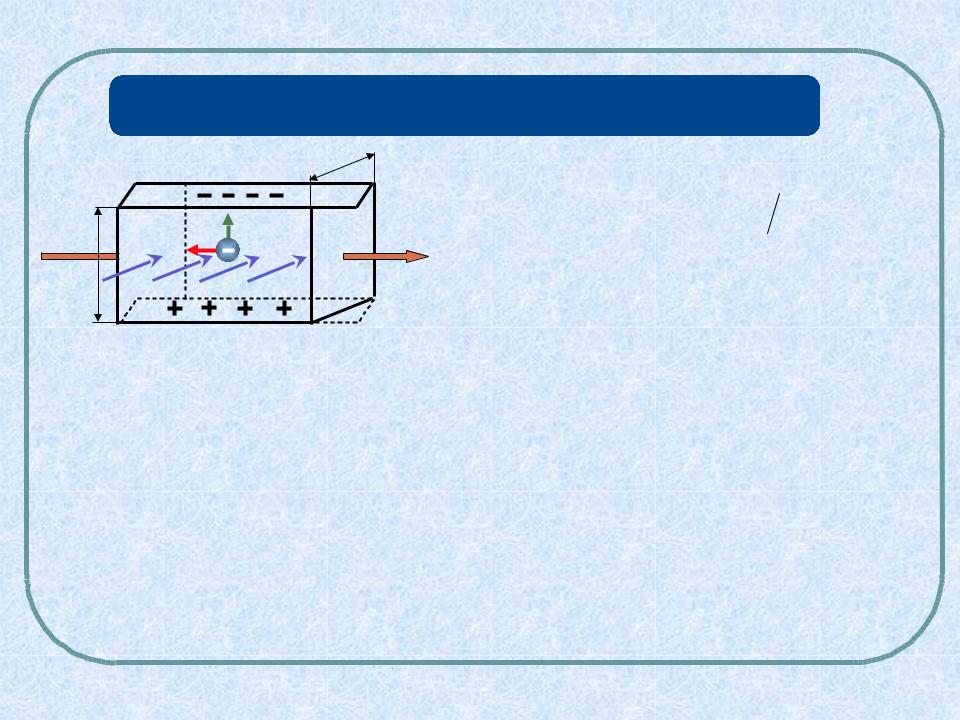
Величина 1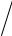
en R - постоянная Холла, зависящая от вещества. Окончательно получим:
I |
выражение для поперечной |
Rd |
холловской разности потенциалов |
Кафедра физики
ЭФФЕКТ ХОЛЛА
d
|
v |
F |
|
|
|
a |
B |
|
|
|
|
I |
1 en R |
|
Rd |
|
j |
|
Примеры использования эффекта Холла.
Знание постоянной Холла позволяет:
а) найти концентрацию и подвижность носителей тока в веществе;
б) судить о природе проводимости полупроводников (знак постоянной Холла совпадает со знаком заряда носителей тока).
Датчики Холла используются для измерения величины магнитного поля, применяются в измерительной технике для иных целей.