4.5 Энергия системы, состоящей из двух заряженных тел.

Рассмотрим 2 тела, создающих соответственно поля и. Тогда в соответствии с принципом суперпозиции:

Возведем это равенство скалярно в квадрат:

Если теперь домножим это выражение на , то два первых слагаемых могут интерпретироваться как объемная плотность энергии электрического поля. Тогда полная энергия системы может быть представлена в виде:

Отметим, что полная энергия системы, собственная энергия первого и второго тел – величины неотрицательные. Если изменяется расположение тел, но не изменяется расположение зарядов на этих телах, то . Поля подчиняются принципу суперпозиции, однако энергия суммы тел не равна сумме энергий отдельных тел.

Для самостоятельного изучения

4.6 Энергия взаимодействия точечного электрического диполя с внешним полем .

Рассмотрим точечный диполь, находящийся во внешнем поле , запишем выражение для нахождения энергии их взаимодействия:

если , то, энергия минимальна

если , то, энергия максимальна.

Мы знаем, что система обычно стремится минимизировать свою энергию, поэтому диполь будет поворачиваться в такое положение, чтобы вектор был направлен по полю, это, очевидно, и будет его устойчивое положение во внешнем поле.

Теперь вернемся к описанию силового (или динамического) действия внешнего поля на диполь. В пункте 4.2 было показано, что на диполь, помещенный в поле действуют сила и момент сил, соответственно равные:

Теперь мы хотим посмотреть на эти выражения с энергетической точки зрения.

_{Получим несколько иное выражение для силы, действующей на диполь, находящийся во внешнем поле.}

Представим несколько иначе , учитывая малость. Введем произвольно ориентированную декартову систему координат, тогда

будет иметь проекции на координатные оси ,и. Если мы теперь мысленно переместимся из отрицательного полюса в положительный полюс, то наше перемещение вдольв декартовой системе координат может быть представлено в виде:

тогда, подставив полученное выражение в исходное, получим:

К полученной формуле можно было прийти и несколько иначе, исходя из формулы, связывающей потенциальную силу и потенциальную энергию:

Рассмотрим теперь связь энергии диполя с моментом сил, действующих на него во внешнем поле. Рассмотрим произвольную ориентацию диполя во внешнем поле в декартовой системе координат. Диполь лежит в плоскостиXY. Поле направлено вдоль оси X. Очевидно момент сил будет направлен вдоль отрицательного направления оси z. Рассчитаем этот момент сил:

Поворачивая диполь в пространстве, изменяя угол , а значит и энергию диполя, получим:

- это и есть модуль момента сил, его направление видно из рисунка. Итак, получаем:

Пункт 5. Проводник в электростатике.

Проводник – это вещество, в котором есть свободные носители электрического заряда, способные двигаться внутри вещества под действием приложенных к ним сил. В металлах это свободные электроны.

Пункт 5.1 Проводник и электростатическое поле.

Свойство1:

Электростатическое поле внутри проводника отсутствует, .

Доказательство:

От противного: если бы в проводнике , то появляется электрический ток, т.к. есть свободные заряды и электрическое поле, которое будет действовать на заряды с некоторой силой. Но тогда это не есть случай электростатики. См. ЭКСПЕРИМЕНТ

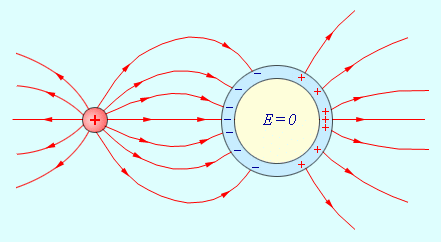
Все внутренние области проводника, внесенного в электрическое поле, остаются электронейтральными. Если удалить некоторый объем, выделенный внутри проводника, и образовать пустую полость, то электрическое поле внутри полости будет равно нулю. На этом основана электростатическая защита – чувствительные к электрическому полю приборы для исключения влияния поля помещают в металлические ящики (рис. ).

Рисунок Электростатическая защита. Поле в металлической полости равно нулю

Свойство2:

Внутренняя область проводника и его поверхность эквипотенциальны. См. ЭКСПЕРИМЕНТ

Доказательство:

В силу первого свойства внутри и на поверхности проводника , с другой стороны, или, т.е., значит, потенциал не является функцией точки, он одинаков везде внутри проводника и на его поверхности.

Свойство3:

Внутри проводника (объёмная плотность заряда).

Доказательство:

Доказательство формально: т.к., то из теоремы Гаусса в дифференциальной форме, т.к., то и, а значит и.

Свойство4: (Электростатическое поле вблизи заряженной поверхности проводника вне проводника):

См. ЭКСПЕРИМЕНТ

Изобразим на рисунке сечение поверхности проводника плоскостью листа. Допустим на проводнике имеется некоторый избыточный положительный заряд, т.е. не хватает электронов. Все эти положительные заряды сосредоточатся на поверхности с поверхностной плотностью . Выберем гауссову поверхность в виде небольшого цилиндра маленькой высоты так, как он изображен на рисунке. Этот цилиндр вырезает из поверхности проводника вместе с расположенными на нем зарядами некоторый фрагмент площади. Применим теорему Гаусса. Поле внутри проводника = 0, поэтому и поток через нижний торец тоже равен нулю. Поток через верхний торец будет равен.Поток через боковую поверхность будет равен нулю, поскольку мы выбрали элементарный, очень маленький цилиндр, а также потому, что поле в точках этой поверхности перпендикулярно вектору нормали к поверхности.

,

Мы можем также использовать также и теорему о циркуляции электрического вектора: выберем замкнутый контур, лежащий в плоскости листа так, как это показано на рисунке, и пройдем по этому контуру, скажем, по часовой стрелке. Мы знаем, что циркуляция электрического поля в этом контуре = 0. На верхнем участке вклад в циркуляцию даст только скалярное произведение векторана вектор перемещения, перемещение происходит вдоль касательной (тангенциальная составляющая), а три других вклада равны нулю: перпендикулярные к поверхности проводника - потому что перпендикулярная составляющая к перемещению очень мала, а вклад участочка, находящегося внутри проводника = 0, поскольку поле там = 0. Тогда по теореме о циркуляции:

,

Таким образом, мы приходим к выводу, что если у нас есть проводник произвольной конфигурации, он заряжен, и состояние этого проводника электростатическое, т.е. заряды на нем покоятся, то снаружи проводника поле есть, и вблизи поверхности проводника это поле направлено перпендикулярно к поверхности.

Замечание: Поле создано не только зарядом, действительно:

Исходя из принципа суперпозиции, можно записать:

, (1)

Интересно, что вклады в общую напряженность поля от маленькой поверхности и от всей остальной поверхности проводника одинаковы. Получается, в самом деле, что поле вблизи поверхности проводника создается не только зарядом, попавшим в гауссову поверхность.

ЕЩЕ РАЗ ПОДРОБНЕЕ Итак, мы имеем поля вблизи поверхности проводника

Несмотря на то, что поле в (2) зависит только от локальной плотности заряда, создается это поле всеми зарядами рассматриваемой системы. Чтобы сделать данное замечание более ясным, проведем анализ выражения (2) на основе принципа суперпозиции. Поле вблизи поверхности проводника (2) равно сумме поля , создаваемого остальными зарядами (расположенными вне элемента поверхности ), и поля, создаваемого зарядами, локализованными на поверхности . Поле в точках вблизи поверхности (здесь она ведет себя как бесконечная однородно заряженная плоскость) равно

В силу суперпозиции полей и

(3)

Рис 2. Поле , созданное заряженным проводником вблизи его поверхности (вне проводника). Изображены также векторы  - поля, созданного всем поверхностным зарядом, кроме расположенного на , а также (вне проводника) и (внутри проводника) - полей, созданных зарядом элемента поверхности

Из условия _внутр = 0 получаем вновь (2), так как из второго равенства (3) следует .