2.7.ВЫЧИСЛЕНИЕ ПО
ИЗВЕСТНОМУ E ПОТЕНЦИАЛА
Рассмотрим несколько примеров вычисления разности потенциалов между точками поля, созданного некоторыми заряженными телами
1
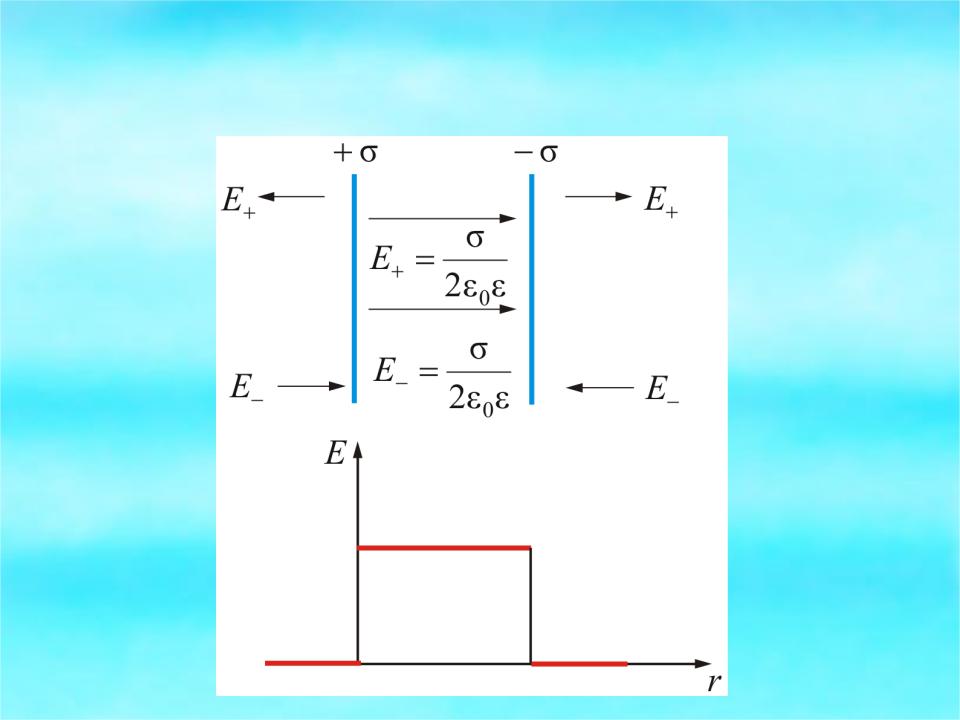
2.7.1. Разность потенциалов между двумя бесконечными заряженными плоскостями
2
Мы показали, что напряженность связана с
|
потенциалом |
|
|
|
E dφ |
, |
тогда dφ Edl |
|
dl |
|
(2.17) |
E |
σ |
|
|
ε0 – напряженность |
|||
где |
|||
электростатического поля между заряженными плоскостями
σ = q/S – поверхностная плотность заряда.
3
Чтобы получить выражение для потенциала между плоскостями, проинтегрируем выражение dφ Edl
|
2 |
|
|
σ |
|
x2 |
|
|
|
|
dφ |
|
|
|
dx; |
|
|
||
|
|
|
|
|
|
|
|||
|
|
|
|
ε0 |
|
|
|
|
|
1 |
|
|
|
x |
|
|
|||
|
|
|
|
σ |
1 |
|
|
||
|
φ2 φ1 |
|
|
x2 x1 |
|
||||
|
|
|
|
|
|||||
|
|
|
|
|
|
||||
|
|
ε0 |
|
|
|
|
|||
|
|
|
|
|
σd |
|
|||
При x1 |
= 0 и x2 = d |
φ |
2 |
|
φ |
(2.18) |
|||
|
|
|
|
|
1 |
ε0 |
|
||
|
|
|
|
|
|
|
|
|
|
4
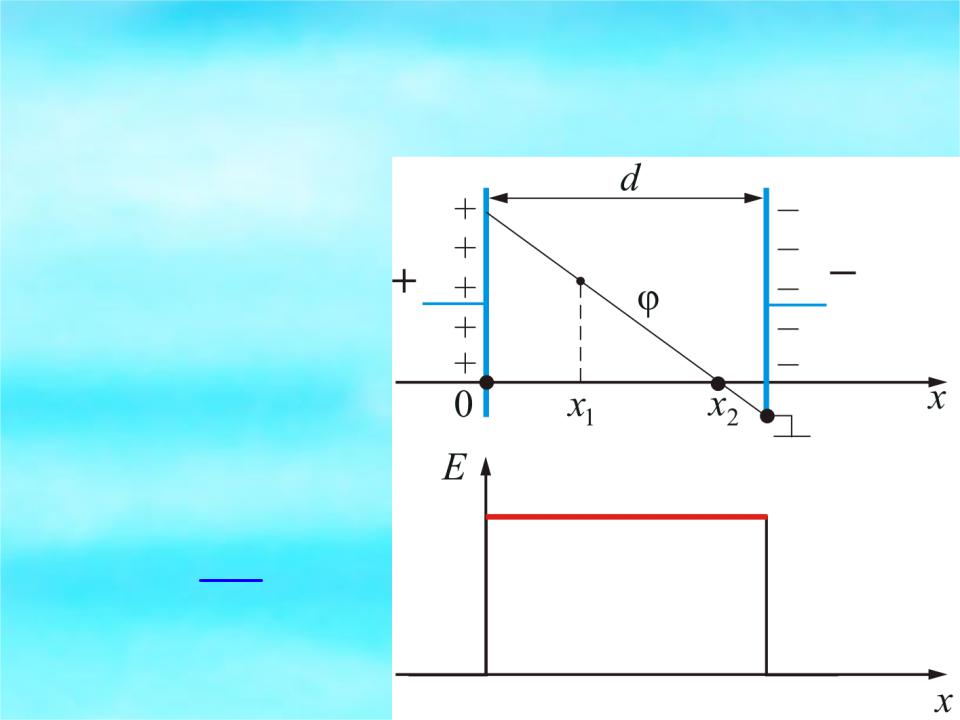
На рисунке изображена зависимость напряженности E и потенциала φ от расстояния между плоскостями.
φ2 φ1 σd
ε0
E 0
5
2.7.2. Разность потенциалов между точками поля, образованного бесконечно длинной цилиндрической
поверхностью
С помощью теоремы Остроградского- Гаусса мы показали, что
|
|
|
|
|
|
|
|
|
|
|
0 внутри цилиндра, т.к. там нет зарядов |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
λ |
|
|
или |
q |
|
на поверхности цилиндра |
|
E |
|
|
|
|
|
|
|||
|
2πε |
0R |
2πε0Rl |
||||||
|
|
|
|
|
|||||
|
|
λ |
|
|
или |
|
q |
вне цилиндра. |
|
|
|
|
|
|
|
|
|||
|
2πε |
0r |
2πε0rl |
||||||
|
|
|
|
6 |
|||||
Тогда,т.к. |
2 |
λ |
|
r2 |
|
dφ Edr; |
dφ |
|
dr |
||
2πε |
|
||||
|
1 |
0 r |
r |
||
|
|
|
1 |
|
|
отсюда следует, что разность потенциалов в произвольных точках 1 и 2 будет равна:
|
φ |
2 |
φ |
|
|
|
1 |
||
|
|
|
λ |
|
|
|
|||
|
|
|
|
|
|
2πε0 |
|||
|
|
|||
|
|
|
||
|
φ |
λ |
|
|
|
|
|
||
|
|
|
2πε0 |
|
|
|
|
||
ln R1 ln Rr
λ |
|
ln |
r2 |
|
q |
|
|
ln |
r2 |
|
2πε |
0 |
r |
2πε |
0 |
l |
r |
||||
|
|
|
||||||||
|
1 |
|
|
|
1 |
|||||
const внутри и на поверхност
вне цилиндра.
7
|
|
|
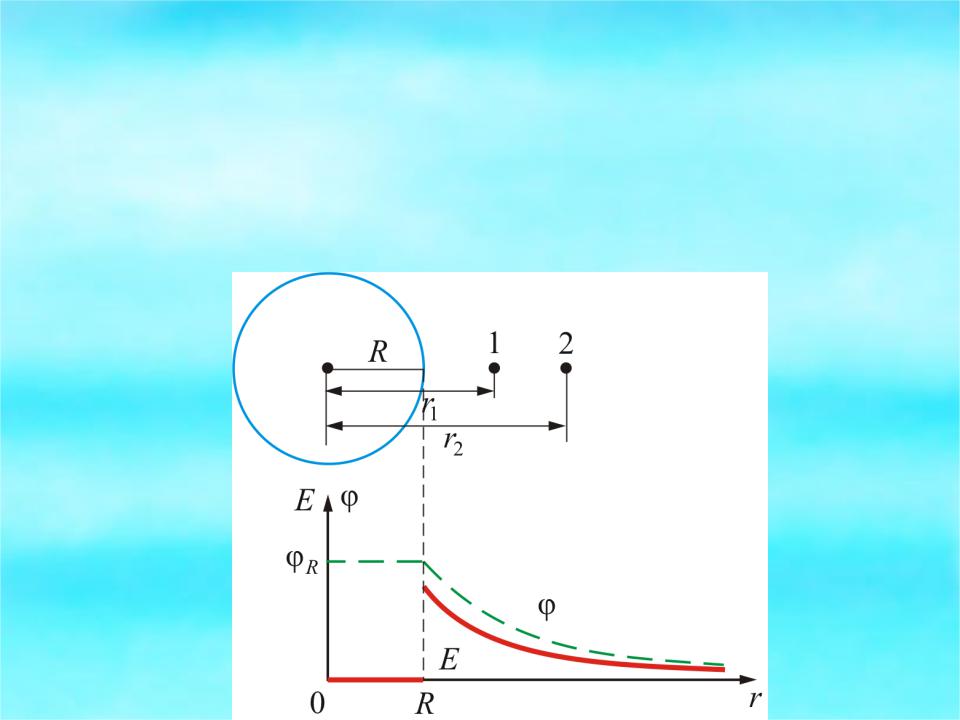
ln |
1 |
const внутри и на поверхности |
|
|
|
|
|
|
||
|
|
|
R |
|||
|
|
|
|
|||
2 0 |
|
|
||||
|
цилиндра |
|||||
|
||||||
|
|
|
|
r |
|
|
|
|
|
ln |
вне цилиндра. |
||
|
|
|
||||
2 |
|
R |
||||
|
|
0 |
|
|
|
|
|
|
|
|
|
||
8
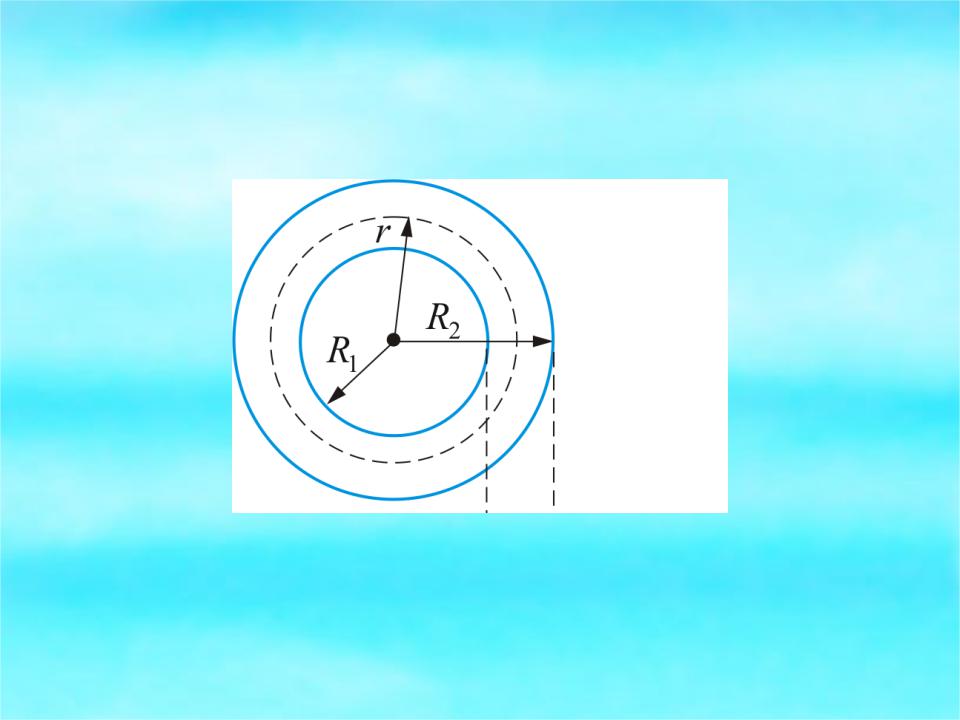
2.7.3. Разность потенциалов между
обкладками цилиндрического конденсатора
|
0 внутри меньшего и вне большего цилиндров зарядов нет |
|||
|
λ |
|
|
|
E |
между цилиндрами, когда R1 |
r R2. |
||
|
|
|||
2πε0r |
||||
|
|
|
||
9
Т.к. |
dφ Edr , то |
|
|
|
|
φ2 φ1 |
λ |
|
ln r2 |
2πε |
|
|||
|
|
0 |
r1 |
|
λ |
|
|
ln |
R2 |
const внутри меньшего цилиндра (r R |
|
|
|
||||
2πε |
0 |
|
|
R |
1 |
|
|
|
|
|
1 |
|
|
λ |
|
|
|
r |
|
|
|
|
|
|
|
||
φ |
|
|
|
ln |
|
между цилиндрами (R1 r R2 ) |
2πε |
0 |
|
R |
|||
|
|
|
|
1 |
|
|
|
0 |
|
вне цилиндров. |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10
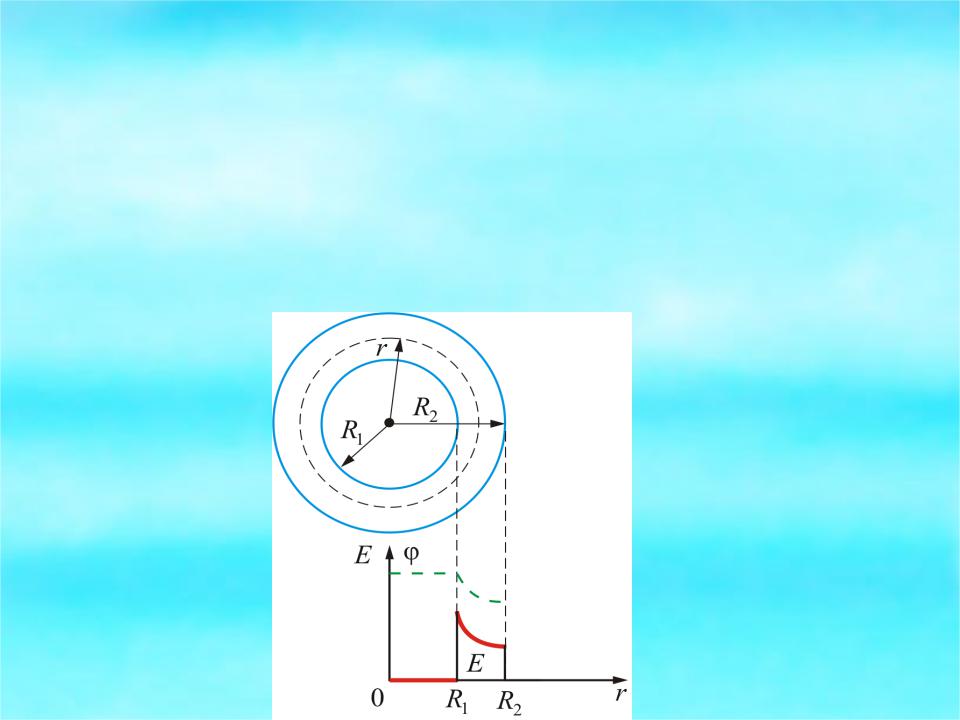
Таким образом, внутри меньшего цилиндра имеем , Е = 0, φ = const;
между обкладками потенциал уменьшается по
логарифмическому закону,
вторая обкладка (вне цилиндров) экранирует электрическое поле и φ и Е равны нулю.
11