1.5. Примеры расчета электростатических полей в вакууме 1.5.1. Поле заряженной нити (стержня)
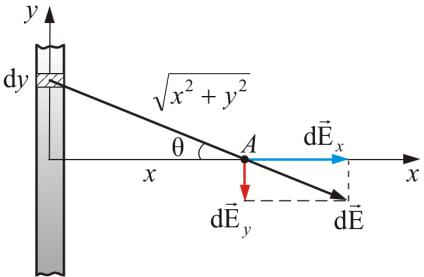
Определим напряженность электрического поля в точке А на расстоянии х от бесконечно длинного, линейного, равномерно распределенного заряда.
λ – заряд, приходящийся на единицу21
Считаем, что х – мало по сравнению с длиной проводника. Элемент длины dy, несет заряд dq = dy λ. Создаваемая этим
элементом напряженность |
||||
1 |
|
dy |
||
электрического поля в точке А: |
||||
dE |
|
|
|
. |
4 0 |
( x2 y2 ) |
|||
|
|
22 |
||
r
ВекторdE
причемdE dE
x
имеет проекции dEx и dEy |
|
cosθ; |
dEy dE sin θ. |
Т.к. проводникr бесконечно длинный, а задача симметричная,dE то у –
компонента вектора |
обратится в |
ноль (скомпенсируется), т.е. . |
|
Ey |
dE sin 0 |
23
Тогда |
|
E Ex dEcos |
|
|
|
|
|
cos dy |
|
|||||||||
|
4 0 |
|
|
x2 y2 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
Теперь выразим y через θ. Т.к. |
|
|
|
y xtg , |
|||||||||||||
То |
|
|
|
dy xd / cos2 и |
( x2 y2 ) x2 / cos2 |
|||||||||||||
|
|
|
тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
E |
|
|
1 |
2 |
cos d |
|
E |
|
|
|
|
|||||||
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
||||
4 |
|
|
x |
2 x |
2 |
0 x |
||||||||||||
|
|
0 |
|
|
2 |
|
0 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
24
Задание: по тонкому кольцу радиуса R однородно распределен
заряд q. Определить Е в точке А
25
1.5.2. Электростатическое поле
диполя
Электрическим диполем называется система двух
одинаковых по величине, но разноименных
точечных зарядов, расстояние между которыми
значительно меньше расстояния до тех точек, в
которых определяется поле системы
|
Плечо диполя – вектор, направленный от |
||||
|
отрицательного заряда к положительному и |
||||
|
|
|
r |
r |
|
|
численно равный расстоянию между зарядами. |
||||
|
Обозначим |
вектор: |
ql |
– электрический момент |
|
|
|
p |
|
||
|
диполя (или дипольный момент) –rпроизведение |
||||
|
положительного заряда диполя на плечо . |
||||
|
|
|
r |
|
l |
|
|
|
|
r |
|
|
Направление |
p |
|
l |
|
|
|
совпадает с направлением , т.е. от |
|||
|
отрицательного заряда к положительному. |
||||
26
Пример 1. Напряженность поля в точке, |
|
|
|
|
||||||||||||||||||||||
расположенной на оси диполя |
|
|
|
|
|
|
|
|
||||||||||||||||||
|
r |
|
|
|
q |
|
|
|
|
|
|
|
|
|
q |
|
|
|
|
r r |
|
r r |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
E |
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
// |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
||||||
|
|
|
4 0 |
2 |
|
4 0 |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
r |
|
r |
|
|
|
|
r |
r |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||
r r l, |
r r r |
так как далеко находимся
|
r |
|
|
|
q |
|
|
l r 2 |
|
|
|
2 p |
|
||
|
|
|
|
|
|
||||||||||
|
|
|
|
||||||||||||
|
E// |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|||||||||
|
|
4 0 |
r4 |
|
4 0 r3 |
||||||||||
|
|
|
|
r |
|||||||||||
|
|
|
|
||||||||||||
|
|
|
|
|
r |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
2 p |
|
|
|
|||||
или |
|
|
|
E|| |
|
|
|
|
|
. |
|
||||
|
|
|
0 r3 |
|
|||||||||||
|
|
|
|
|
|
4 |
27 |
||||||||
ur |
ur |
|
|
|
E |
|
|||
E |
|
А |
|
r |
r |
ur |
|
|
|
E |
|
r |
r |
|
r |
l |
|
||
|
|
|
|
|
Пример 2. |
|
|
Найдем Е в точке А на прямой, |
|||||||||||||||||||||||||
|
проходящей через центр |
диполя и |
|
|
|
|
|
|
|
|||||||||||||||||||
|
перпендикулярной кl |
оси. |
q |
|
|
|
l |
|
|
|
p |
|
|
|||||||||||||||
|
E |
|
l |
|
E E |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
E |
r |
|
|
4 0r2 |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
ur |
ur |
r |
|
|
|
|
r |
|
4 0r3 |
||||||||||||||||
Из рисунка видно, чтоE |
|
и |
|
|
противонаправлены, след-но |
|||||||||||||||||||||||
|
|
|
ur |
|
1 |
p ur |
|
|
|
|
|
ur |
|
|
|
|
|
|
1 |
|
ur |
|||||||
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
||||||||
|
|
|
|
E |
|
; |
r r; E |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
4 |
|
|
4 |
|
|||||||||||||||||||
|
|
|
|
|
|
|
0 |
|
r3 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
r3 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Пример 3. Найти вектор напряженности поля диполя
в произвольной точке пространства
Получить самостоятельно формулы |
|||||||||||||||
ur |
ur |
ur |
|
|
|
|
1 |
|
|
|
|
|
ur |
|
ur |
E E |
// E |
|
|
|
|
|
|
2 p// p |
|||||||
4 0r |
3 |
|
|||||||||||||
ur |
|
1 |
|
|
|
p, r |
r |
ur |
|
||||||
|
|
|
|
|
|||||||||||
E |
|
|
|
|
3 |
|
|
|
|
|
p |
|
|||
4 0r |
3 |
|
|
r |
2 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
СРС!1.6.Электрический
точечный диполь во внешнем поле.
В однородном поле суммарная сила, действующая на диполь, равна нулю.