Кафедра физики
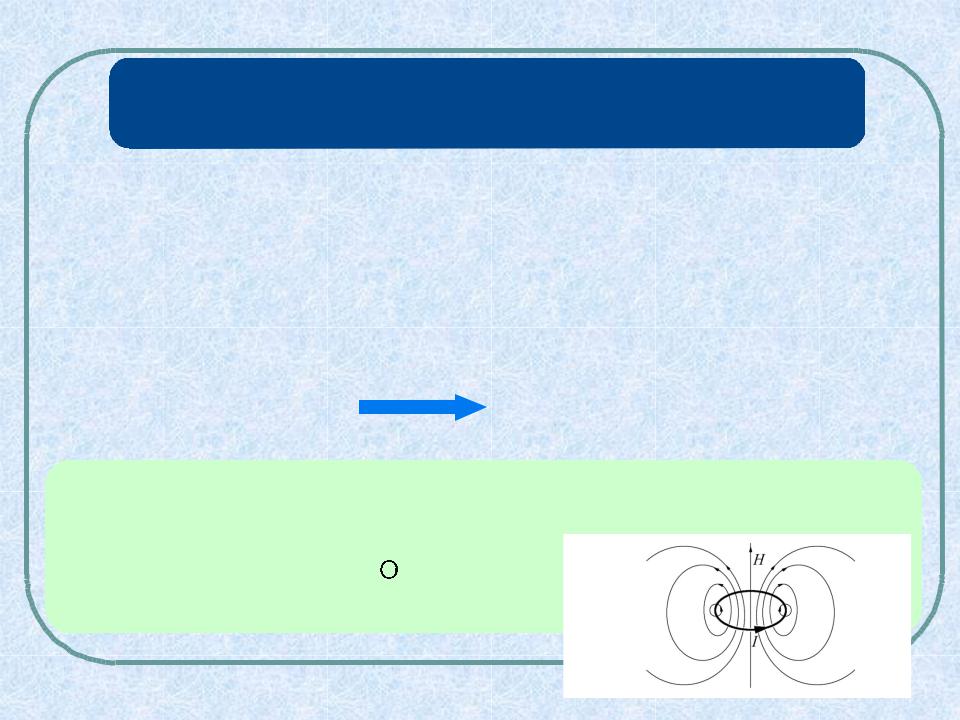
Поток вектора магнитной индукции. Теорема Гаусса-Остроградского для вектора B
Магнитный поток через элемент dSповерхности S соответственно, выражается формулой
dФB B,dS BdS cos
В этой формуле dS dSn , n - орт вектора нормали.
Полный поток через поверхность S равен сумме потоков через все элементы поверхности, т.е. равен интегралу:
Ф B,dS Bd
B n
S S
Если поверхность замкнутая, то Ф BdSB,dS
B n
S S
Кафедра физики
Поток вектора магнитной индукции. Теорема Гаусса-Остроградского для вектора B
Поскольку силовые линии магнитного поля замкнуты, то любая силовая линия пересекает замкнутую поверхность дважды (четное число раз), причем один раз в положительном по отношению к нормали направлении, а другой раз – в отрицательном. Поэтому суммарный магнитный поток, пронизывающий замкнутую поверхность S, всегда оказывается равным нулю:
|
S |
|
теорема Гаусса-Остроградского |
Ф |
B, dS 0 |
||
B |
Ñ |
|
для магнитного поля. |
|
|
|
|
Поток вектора напряженности магнитного поля через любую замкнутую поверхность равен нулю:
B,dS 0
S
|
|
|
|
|
Кафедра физики |
|
Поток вектора магнитной индукции. Теорема |
||||||
Гаусса-Остроградского для вектора |
B |
|||||
Важное следствие |
поток |
вектора |
B |
через |
замкнутую |
|
из теоремы Гаусса: |
поверхность S |
не зависит от формы |
|
|||
|
этой поверхности. |
|
|
|
||
В дифференциальной форме |
divB 0 |
|
|
|||
уравнение Гаусса имеет вид |
|
|
|
|
|
|
Сведения из векторного анализа: … дивергенция характеризует интенсивность (обильность) истоков и стоков векторного поля.
Если divB 0 , это означает, что магнитное поле не имеет стоков и истоков, линии Bзамкнутые. Магнитное поле имеет соленоидальный или вихревой характер.
Физическая причина соленоидальности магнитного поля - отсутствие свободных магнитных зарядов, аналогичных электрическим зарядам.
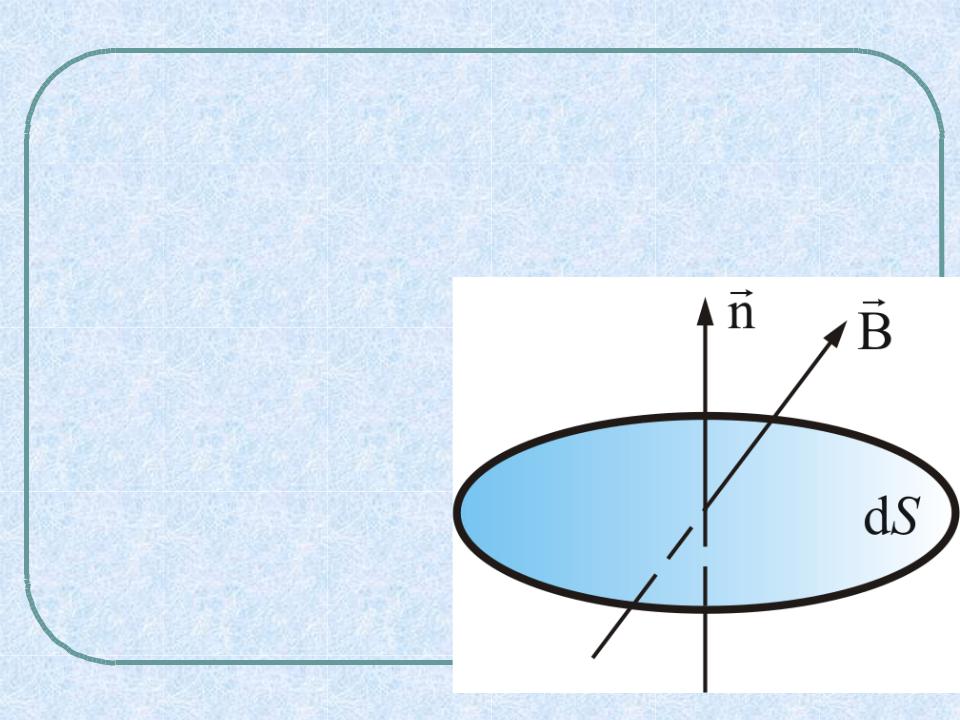
Другое определение: 1 Тл равен магнитнойКафедра физики
индукции при которой магнитный поток сквозь площадку 1 м2, перпендикулярную направлению поля
равен 1 Вб. r r |
|
|
|||
|
S |
|
|
0 |
|
Ф |
|
B, dS |
|
||
B |
Ñ |
|
|
|
|
dФB BdS cos(dn,B)
Ф B n d S .
S
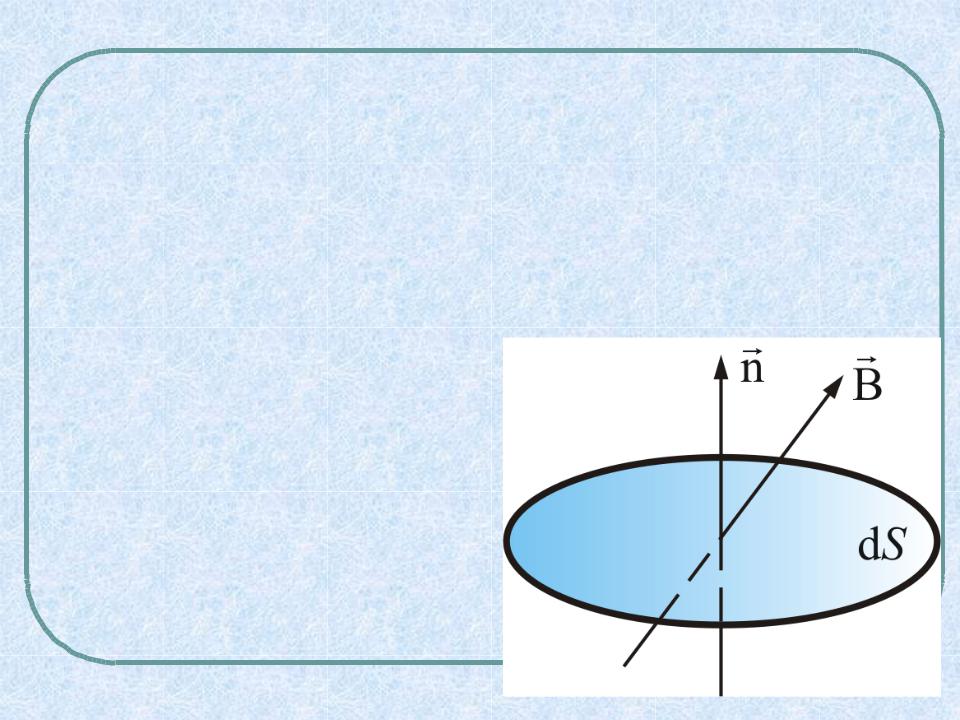
Единица измерения магнитного потока Вб, получилаКафедра физикисвое название в честь немецкого физика Вильгельма Вебера (1804 – 1891 г.) – профессора университетов в Галле, Геттингене, Лейпциге.
Как мы уже говорили, магнитный поток Ф, через поверхность S – одна из характеристик магнитного поля
dФB BdScos(dn, B),
Ф B n d S .
S
Единица измерения магнитного потока в СИ: Кафедра физики
[ФВ ] [B] [S] Тл м2 Вб
1 Тл 1 |
Вб |
1Тл 104 Гс |
м2 |
|
|
1 Вб 104 |
Гс 104 см2 108 Мкс |
|
Здесь Максвелл (Мкс) – единица измерения магнитного потока в СГС названа в честь знаменитого ученого Джеймса Максвелла (1831 – 1879 г.), создателя теории электромагнитного поля.
Напряженность магнитного поля измеряется А·м-
1
1 А м 1 4π 10 3 Э |
1Э 79,6 80 А м 1 |
Кафедра физики
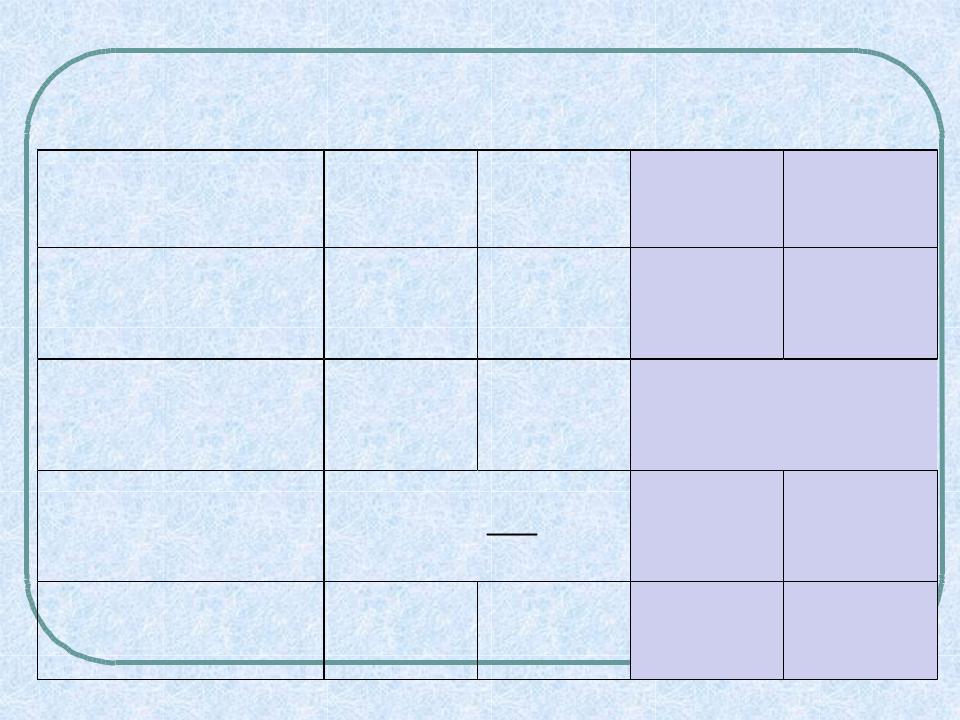
Таблица основных характеристик магнитного поля
Наименование
Магнитная
индукция
Напряженность магнитного поля
Магнитная
постоянная
Поток магнитной индукции
Обозна
чение
В
Н
μ0
ФB
|
СИ |
||
|
|
Н |
|
Тл |
|
|
|
|
|
||
|
|
А м |
|
А/м
АН2 ; Фм
Вб (Тл·м2)
СГС СИ/СГС
Гс 104
Э
4π 10 3 
14π 10 7
Мкс 108
|
|
|
Кафедра физики |
Теорема о циркуляции вектора B |
|||
Циркуляцией вектора |
B по замкнутому контуру L называется |
||
интеграл вида |
B,dl Bdl |
|
|
|
|
|
|
|
|
|
|
|
L |
L |
Bl B cos , - угол |
где dl- вектор элемента длины контура, |
|||
между векторами |
B и dl |
|
|
Циркуляция вектора B по произвольному замкнутому контуру L равна произведению 0 на алгебраическую сумму токов, охватываемых контуром:
B,dl I
0
L
Это закон (теорема) о циркуляции вектора B. Иначе эта теорема называется законом полного тока для магнитного поля в вакууме.
Кафедра физики
Найдем циркуляцию магнитного поля по контуру Г
|
|
|
|
|
ur r |
|
|
|
|
|
Формула |
i B, dr 0 I |
|
|
|
||||||
|
|
|
|
Г |
|
|
|
|
|
|
Справедлива для контура любой формы |
|
|
||||||||
|
|
i |
|
r |
B |
i |
r |
|
0 I |
2 r 0 I |
СГ |
|
B d r |
d r |
|||||||
|
|
|
|
|
|
|
|
|
2 r |
uur |
ur |
r |
|
ur |
uur |
|
|
I |
|
d r d r |
|
|
|
|
|
|
||||||
|
|
|
|
|
I |
|||||
B, d r |
B, d r |
|
|
|
|
|||||
|
|
Г |
|
dr |
||||||
B,dl I
0
L
Кафедра физики
Теорема о циркуляции вектора B
Ток Iв теореме есть алгебраическая сумма токов Ik, охватываемых контуром L:
Ток положительный, если его направление связано с направлением |
||||
обхода по контуру правилом правого винта. Ток противоположного |
||||
направления - отрицательный. |
I1 |
0 |
|
|
|
|
I4 0 |
||
Пример |
|
|
I2 0 |
|
I4 - положительные, |
|
|
|
|
токи I1 , I2 и |
|
|
|
|
ток I3 - отрицательный. Сумма токов: |
|
L |
|
|
Ik 0 I1 I2 |
I3 I4 I2 I3 I4 |
|
|
|
|
I3 |
0 |
||
|
|
|
||
|
|
|
|
Кафедра физики |
|
|
Теорема о циркуляции вектора |
B |
|
Если ток I |
|
|
||
распределен по объему, где расположен |
|
|||
контур |
L, то этот ток можно представить как |
|
I jdS |
|
Интеграл берется по произвольной поверхности S, «натянутой» на контур L.
Плотность тока j под интегралом – это плотность в точке, где расположена площадка dS.
Вектор образуетdS с направлением обхода по контуру правовинтовую систему.
Таким образом, теорема о циркуляции вектора B в общем случае будет выглядеть так:
Циркуляция вектора B не равна нулю. Это означает, что магнитное поле в отличие от электростатического поля
не потенциально.