2 семестр МП / Старые материалы - второй поток / Лекции / Лекция 7.1 Магнитное поле продолжение 2(основная задача магнитостатики)

15

8.6.Основная задача магнитостатики.

В пункте 8.5. было показано, что элемент тока создает в точке наблюдения элементарное магнитное поле:

- закон Био – Савара – Лапласа.

Теперь, принимая во внимание принцип суперпозиции магнитных полей, можно решить основную задачу магнитостатики – по известному распределению токов в пространстве найти вектор в интересующей нас точке наблюдения.

Подробно решение этих задач приведено в книжке Гайдуков Г.Н., Овчинников А.С. Электричество и магнетизм. Электромагнетизм. - М.: МИЭТ, 1997. (часть 2) на стр.55-58)

Пример 1 Поле отрезка прямолинейного проводника с током ( в книге пример 4)

Вид конечной формулы будет зависеть от выбора системы координат (отсчета углов)!!!

(Сравните с Примером 1 из Лекции 1 пункт 1.8.1).

Найдем магнитное поле, создаваемое отрезком прямолинейной нити в точке наблюдения. Разместим отрезок нити параллельно оси x, а точку наблюдения поместим в начало координат.

По закону Био – Савара – Лапласа

,

а сам вектор направлен за лист.

, или .

Тогда наше выражение для принимает вид:

.

Точно также, как в предыдущем пункте получается поле для бесконечно длинной нити, для нее; тогда поле бесконечной нити:

Если электростатическую формулу умножить на и заменить на , а на , то

.

Такие замены естественны, если мы пересядем в систему отсчета, движущуюся вдоль заряженной нити со скоростью V, тогда в этой системе отсчета нитка будет двигаться в противоположную сторону со скоростью V и будет представлять собой ток, , и в этой системе отсчета будет регистрироваться магнитное поле, которое можно посчитать, воспользовавшись одним из частных случаев преобразования полей, рассмотренным ранее.

Пример 2 (Магнитное поле на оси кругового тока. На Рис. 1.1 показан вектор от одного элемента тока . Ток I течет по тонкому кольцу радиусом R. Ось Z расположена перпендикулярно плоскости кольца, и ее начало (точка 0) совпадает с центром кольца.

От всех элементов тока будет образовываться конус векторов (Рис. 1.2). Из симметрии конуса видно, что результирующий вектор направлен вдоль оси Z. Поэтому для нахождения его модуля достаточно сложить проекции векторов на ось Z. Проекция dB_z от одного элемента тока Idl в соответствии с законом Био-Савара определяется как

  .

Рис. 1.1. Вектор и его проекция dB_z на ось Z кольцевого тока I.  Элементарное поле cоздается элементом тока

Рис. 1.2. Множество элементарных векторов , созданных в точке наблюдения А (см. Рис. 1.1) элементами тока кольца, и их сумма - вектор

Интегрирование последнего выражения по всем элементам кольца с учетом соотношений  sin  = R / r  и    дает окончательно

 

Отсюда следуют два важных частных случая:

1) магнитное поле в центре кольца (z = 0)

 

2) магнитное поле вдали от кольца (z >> R)

  

Если, введем по определению величину (модуль) магнитного момента кольца с током (см. пункт 8.7 - характеристика петли с током, называется магнитным моментом, по определению , где .

Направление связано с направлением тока в контуре правилом правого винта.)

В нашем случае: 

 m =  R²I  .

Тогда последний результат принимает вид

 

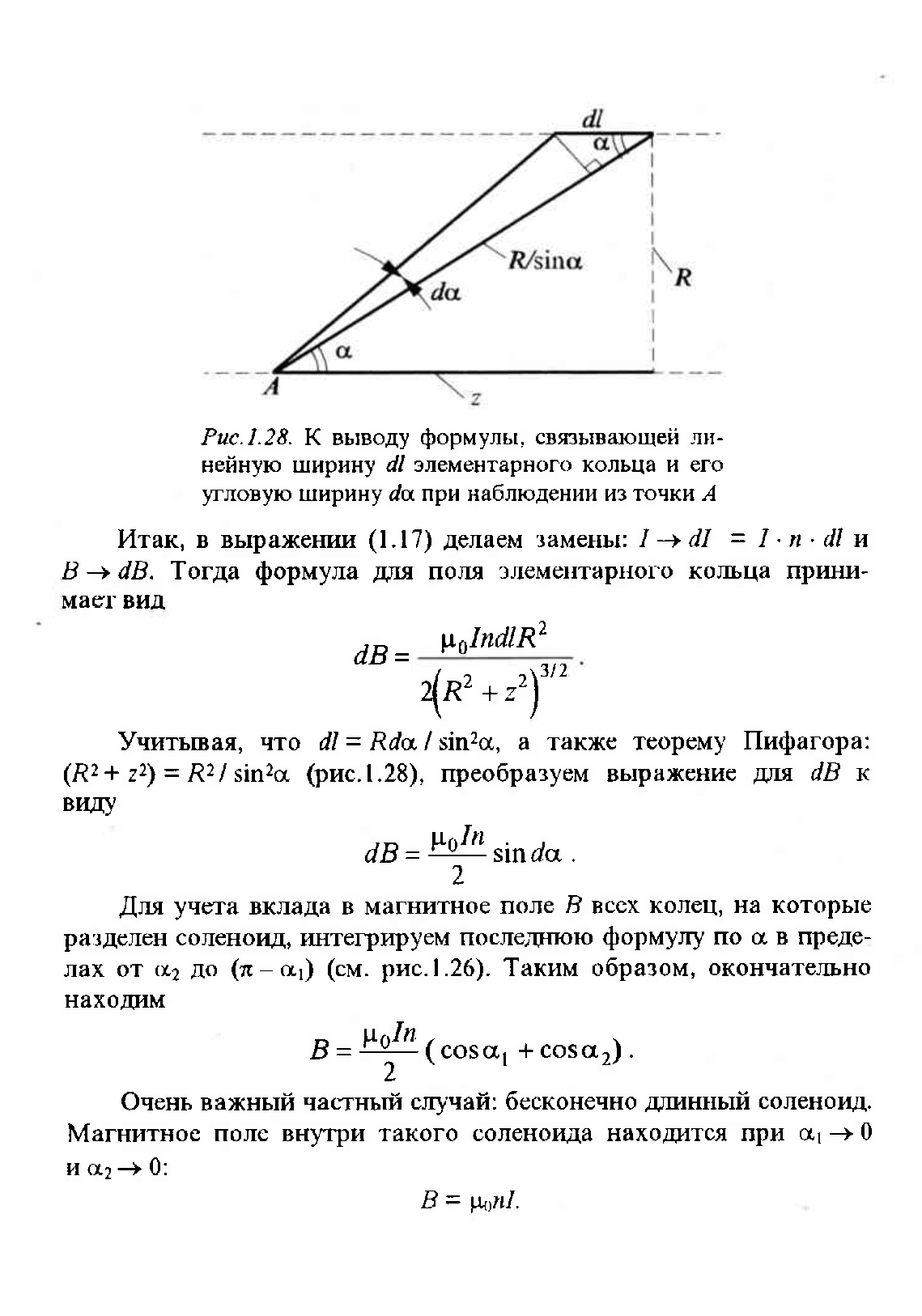
Пример 3. Поле на оси соленоида конечной длины ( в книге - пример 5)