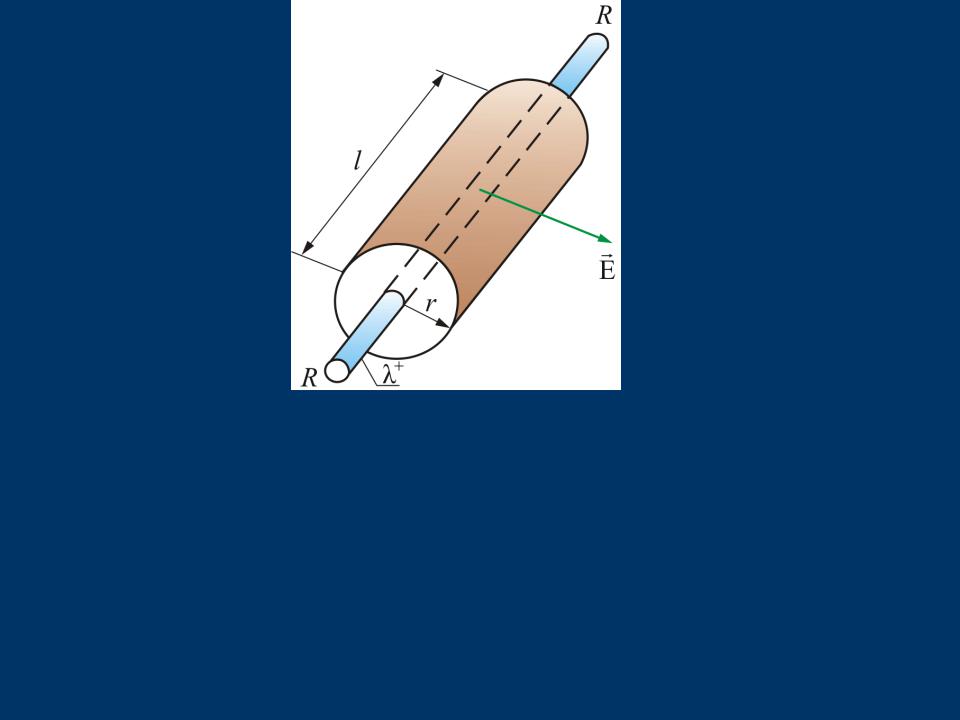
Для оснований цилиндров En 0, |
|
для боковой поверхностиEn E(r), |
т.е. |
зависит от расстояния r. |
|
Следовательно, поток вектора через рассматриваемую поверхность, равен
ФE E(r)S E(r)2πrl. 42
При r R,на поверхности будет заряд q λl.
По теореме Остроградского-ГауссаE(r)2πrl λl
ε0λТогда
Е(r) 2πε0r при r R
Если |
r R, |
E(r) 0, т.к. внутри |
|
замкнутой поверхности зарядов нет. |
43 |
||
|
|
|
|
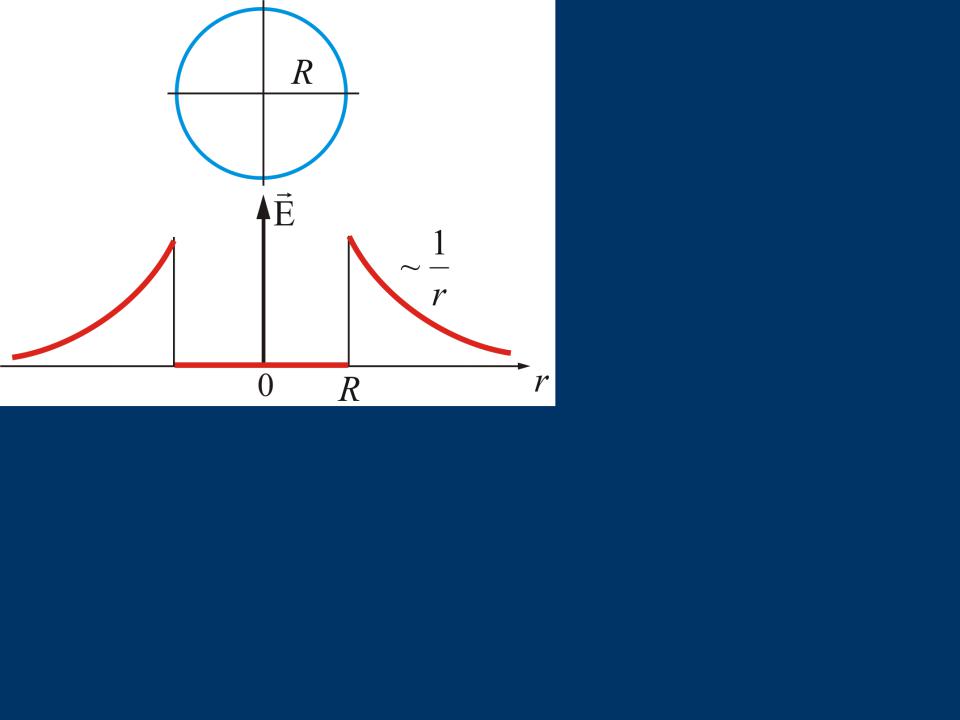
График
распределения напряженности электростатическ ого поля цилиндра
|
|
|
|
|
|
|
|
|
|
|
|
внутри цилиндра, т.к. там нет зарядов |
|||||||||
0 |
||||||||||
|
|
|
|
|
|
q |
|
|
|
|
E |
|
|
|
|
или |
|
|
|
на поверхности цилиндра |
|
|
|
|
|
2 0 Rl |
||||||
2 0 R |
|
|
|
|||||||
|
|
|
|
или |
|
q |
|
|
вне цилиндра |
|
|
|
|
|
|
|
|
|
|
||
|
|
r |
2 |
rl |
||||||
2 |
|
|
||||||||
|
0 |
|
|
|
|
0 |
|
|
|
|
44
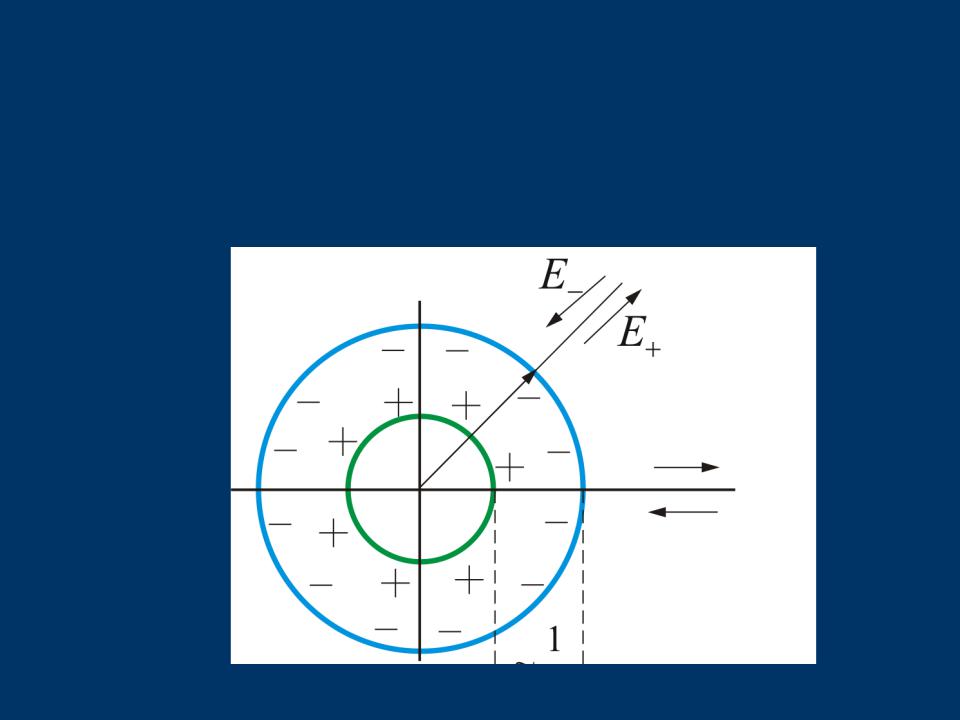
3.5.4. Поле двух коаксиальных
цилиндров с одинаковой линейной плотностью λ, но разным знаком
45
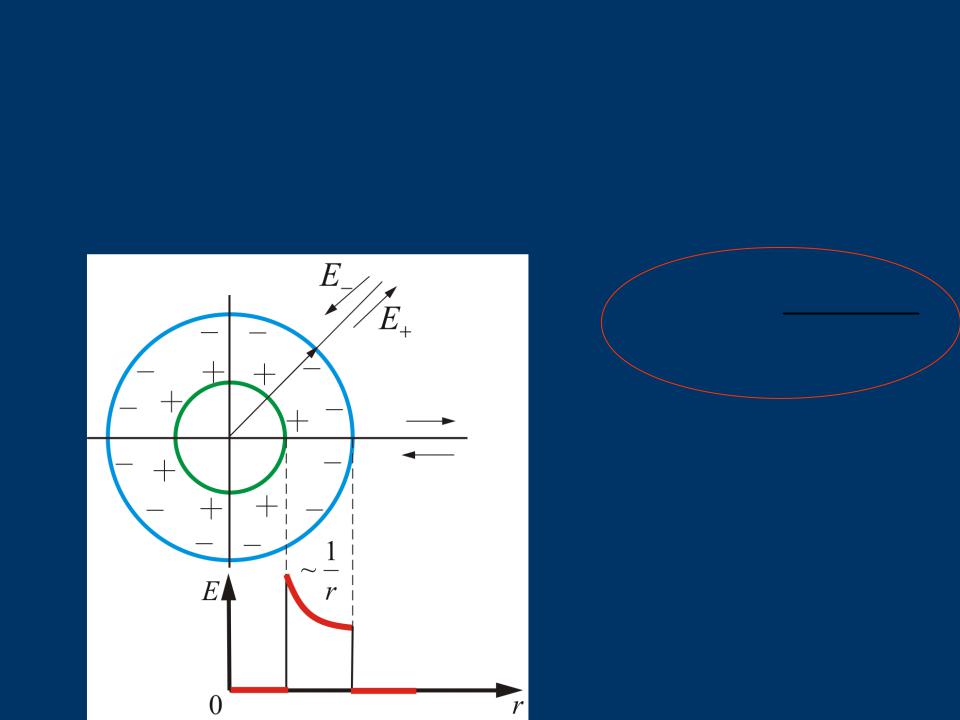
Внутри меньшего и вне большего цилиндров поле будет отсутствоватьE 0
В зазоре между цилиндрами, поле определяется так же, как в п. 3.5.3:
E(r) 2πελ 0r .
46
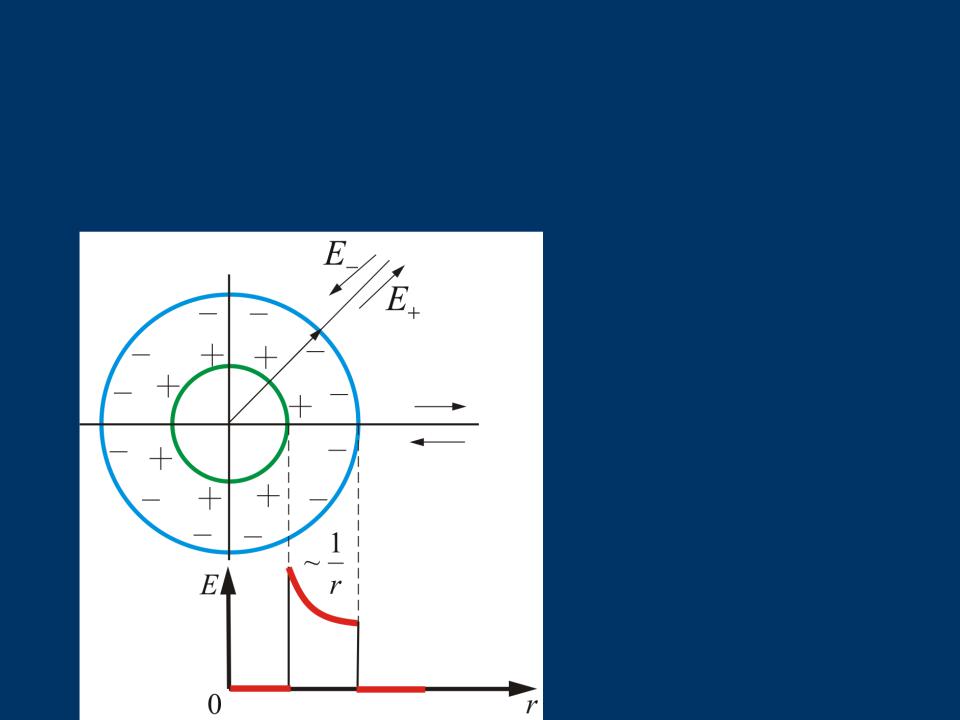
Таким образом для коаксиальных цилиндров
имеем: |
|
|
||
|
0 внутри меньшего и вне большего цилиндров зарядов не |
|||
|
λ |
|
|
|
E |
между цилиндрами, когда R1 |
r R2 |
||
|
|
|||
2πε0r |
||||
|
|
|
||
Это справедливо и для бесконечно длинного цилиндра, и для цилиндров конечной длины, если зазор между цилиндрами намного меньше длины цилиндров (цилиндрический конденсатор). 47
3.5.5. Поле заряженного пустотелого шара
(сферы)
48
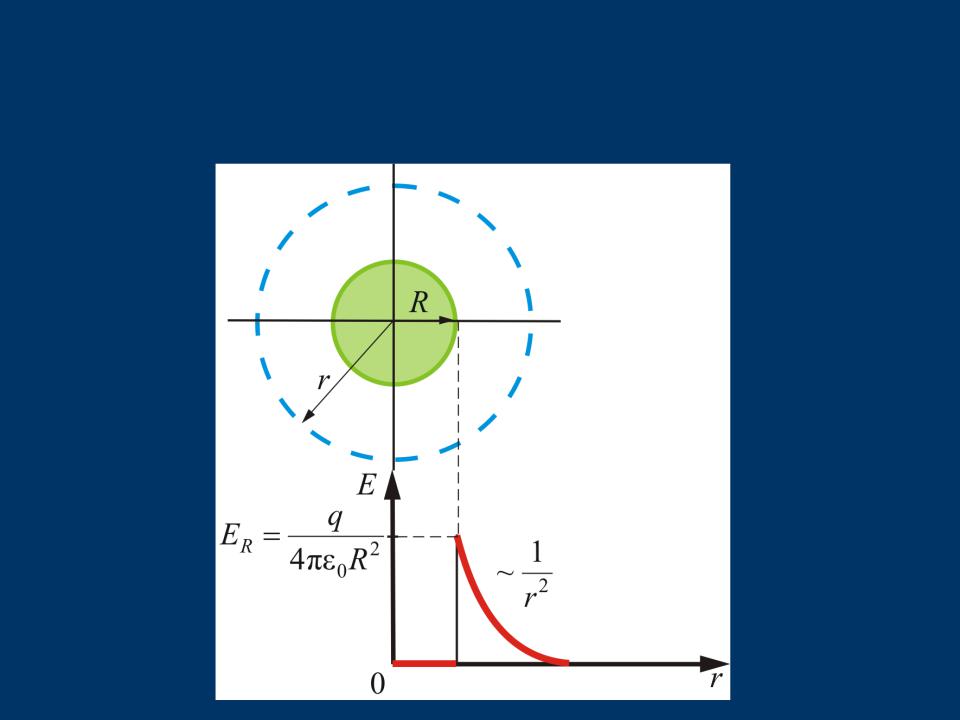
Вообразим вокруг шара – сферу радиуса r (рис).
49
Если r R,то внутрь воображаемой сферы попадет весь заряд q, распределенный по сфере, тогда
ФE E(r)S Е(r)4πr2 εq
0
откуда поле вне сферы:
E(r) q 2 . 4πε0r
Внутри сферы, при r R, поле будет равно нулю, т.к. там нет зарядов: E(r) 0.
50
Как видно, вне сферы поле
тождественно полю точечного заряда той же величины, помещенному в центр сферы.
E |
|
q |
. |
|
4πε0r2 |
||
|
|
|
51