
- •четверг 11 Июль, 2019
- •Тема 3. ТЕОРЕМА ОСТРОГРАДСКОГО- ГАУССА
- •3.1. Силовые линии
- •Остроградский Михаил Васильевич (1801
- •Гаусс Карл Фридрих (1777 – 1855)
- •силовые линии – это линии, касательная к которым в любой
- •В случае точечного заряда, линии напряженности исходят из положительного заряда и уходят в
- •если на рисунке выделить
- •3.2. Поток вектора
- •Для первого рисунка – поверхность А1 окружает
- •3.3. Теорема Остроградского-
- •поток вектора напряженности через произвольную элементарную площадку dS будет равен:
- •Подсчитаем поток вектора через
- •Центр сферы совпадает с центром
- •Тогда поток через S
- •Из непрерывности линии
- •Для любого числа произвольно
- •Полный поток проходящий через S3, не
- •Таким образом, для точечного заряда q, полный поток через любую
- •Электрические заряды могут быть «размазаны» с некоторой объемной плотностью различной в разных местах
- •Суммарный заряд объема dV будет равен:
- •3.4. Дифференциальная форма теоремы Остроградского-Гаусса
- •Теперь устремим V 0, стягивая его к интересующей нас точке. Очевидно, что при
- •Итак,
- •Сам по себе оператор смысла не
- •3.5.Вычисление электрических полей
- •Представим себе цилиндр с образующими,
- •Суммарный поток через замкнутую поверхность (цилиндр) будет равен: ФЕ 2 SE.
- •3.5.2. Поле двух равномерно заряженных плоскостей
- •Результирующее поле, находится как суперпозиция полей, создаваемых каждой из плоскостей.
- ••Распределение напряженности
- •3.5.3. Поле заряженного бесконечного цилиндра (нити)
- •Представим вокруг цилиндра (нити)
- •Для оснований цилиндров En 0,
- •При r R,на поверхности будет заряд q λl.
- •График
- •3.5.4. Поле двух коаксиальных
- •Внутри меньшего и вне большего цилиндров поле будет отсутствоватьE 0
- •Таким образом для коаксиальных цилиндров
- •3.5.5. Поле заряженного пустотелого шара
- •Вообразим вокруг шара – сферу радиуса r (рис).
- •Если r R,то внутрь воображаемой сферы попадет весь заряд q, распределенный по сфере,
- •Как видно, вне сферы поле
- •3.5.6. Поле объемного заряженного
- •Внутри шара при r R,сферическая
- •Т.е. внутри шара
- •Таким образом, имеем:
- •3.8. Уравнения Пуассона (1812 г) и Лапласа (1782 г).
- •Если между проводниками нет зарядов, т.е. 0 , то уравнение Пуассона переходит в
- •Пример. (Иродов 3.49)
- •Thursday, July 11, 2019
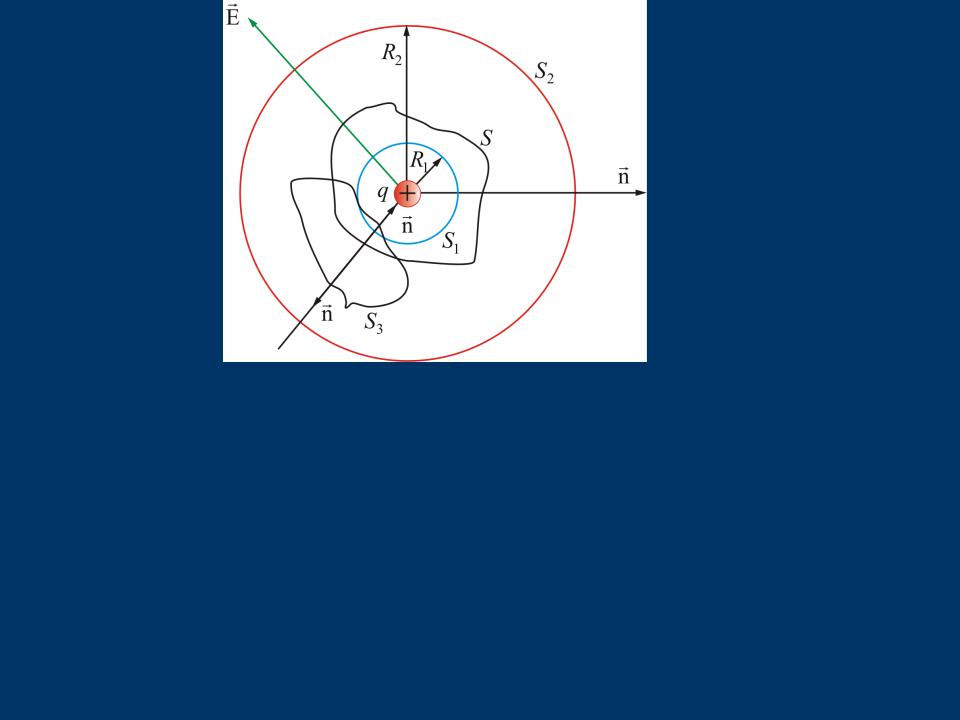
Из непрерывности линии |
E |
следует, что |
|||||
поток и через любую произвольную |
|||||||
поверхность S будет равен этой же |
|||||||
величине: |
|
|
|
|
|
|
|
ФЕ |
r r |
|
|
|
|
|
|
|
ЕdS Еn dS q |
|
|||||
|
Ñ |
|
Ñ |
|
0 |
|
|
|
S |
|
S |
|
|
||
– теорема Гаусса для одного заряда. 22

Для любого числа произвольно |
||
расположенных зарядов, |
||
находящихся внутри поверхности: |
||
|
r r |
q |
ЕdS |
||
Ñ |
|
0 |
S |
|
|
– теорема Гаусса для нескольких
зарядов:
Поток вектора напряженности электрического поля через замкнутую поверхность равен алгебраической сумме всех зарядов, расположенных внутри поверхности, деленной на ε0.
23
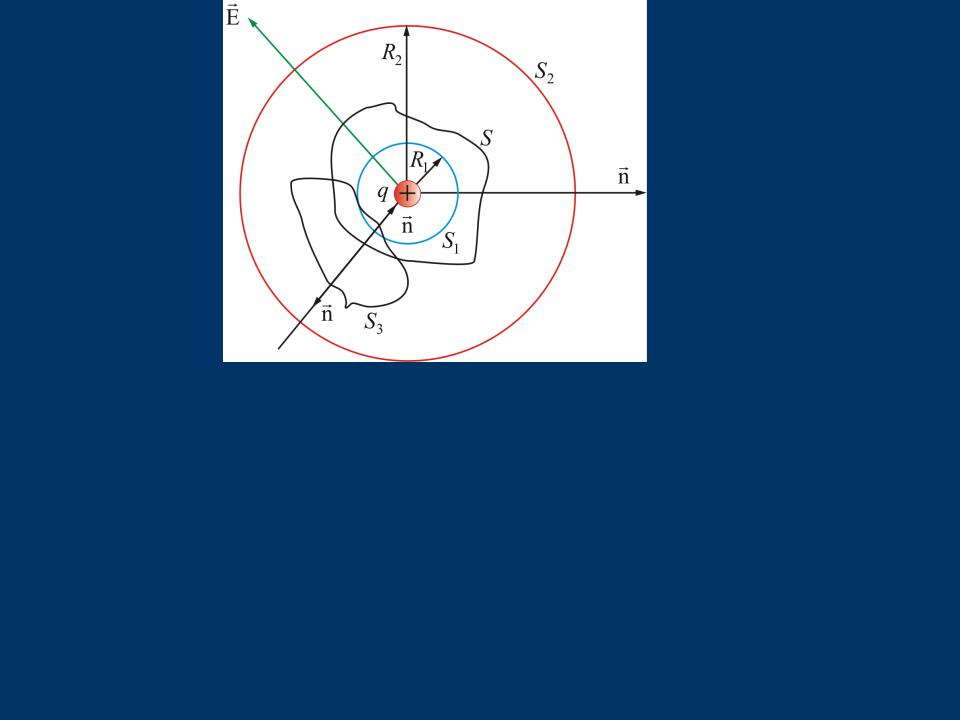
Полный поток проходящий через S3, не
охватывающую заряд q, равен нулю:
Ф3 0
24

Таким образом, для точечного заряда q, полный поток через любую
замкнутую поверхность S будет
равен:
ФЕ εq0 – если заряд расположен внутри замкнутой поверхности;
ФЕ 0– если заряд расположен вне замкнутой поверхности;
этот результат не зависит от формы
поверхности, и знак потока совпадает со знаком заряда.
25

Электрические заряды могут быть «размазаны» с некоторой объемной плотностью различной в разных местах пространства:
|
V – физически бесконечно малый |
|
|
Здесь d |
ρ dq / dV |
|
объем, под которым следует понимать такой объем, который с |
|
одной стороны достаточно мал, чтобы в пределах его плотность заряда считать одинаковой, а с другой – достаточно велик, чтобы не могла проявиться дискретность заряда, т.е. то, что любой заряд кратен целому числу элементарных зарядов электрона или протона .
26

Суммарный заряд объема dV будет равен:
qi ρdV .
|
V |
|
|
Тогда из теоремы Гаусса можно получить: |
|||
|
r r |
1 |
|
|
ФE Ñ(ЕdS) |
dV |
|
|
|
||
|
S |
ε0 V |
|
1
ε0 V ρdV
– это ещё одна форма записи теоремы Остроградского-Гаусса, если заряд
неравномерно распределен по объему.
27

3.4. Дифференциальная форма теоремы Остроградского-Гаусса
Пусть заряд распределен в пространстве V, с объемной плотностью ρ . Тогда
r r |
q |
|
Ñ( EdS ) |
||
ε0 |
||
|
r r |
V |
1 |
r r |
|
|
Ñ( EdS ) |
|
Ñ( EdS ) |
|
||
V |
0 |
||||
|
0 |
|
28

Теперь устремим V 0, стягивая его к интересующей нас точке. Очевидно, что при этом ρ будет стремиться к ρ в данной точке, т.е.
ρ ρ . ε0 ε0
Величину, являющуюсяr
пределом отношения Ñ r
(ЕdS )
к V, при V 0 ,
называют дивергенцией поля Е
div E |
29 |

|
Дивергенция поля |
Е |
||||
|
r |
1 |
|
r r |
||
divE lim |
( EdS ). (3.1) |
|||||
|
V |
|||||
|
V 0 |
Ñ |
|
|
||
Аналогично определяется дивергенция любого другого векторного поля.
Из этого определения следует, что
дивергенция является скалярной
функцией координат.
В декартовой системе координат |
|
||||||
|
E |
x |
Ey |
|
E |
z . |
|
div E |
|
|
|
|
|
||
|
y |
|
|
||||
|
x |
|
z |
30 |
|||
|
|
|
|
|
|
|
|

Итак, |
|
|
|
|
|
|
ρ |
|
|
|
|||
|
div E |
. |
|
|
|||||||||
|
|
(3.2) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
ε0 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Это теорема |
|
|
||||||||||
|
Остроградского-Гаусса в |
|
|||||||||||
|
дифференциальной форме. |
||||||||||||
Написание многих формул |
|
||||||||||||
|
упрощается, если ввести |
|
|
||||||||||
|
векторный дифференциальный |
||||||||||||
|
оператор |
(Набла) |
|
|
|||||||||
|
|
|
r |
|
r |
|
|
r |
|
|
|||
|
|
|
i |
|
j |
|
|
|
k , |
|
|
||
|
x |
y |
z |
|
– орты |
||||||||
|
|
|
|
|
|
где i, j, k |
|||||||
|
осей (единичные векторы). |
31 |
|||||||||||
