
- •четверг 11 Июль, 2019
- •Тема 3. ТЕОРЕМА ОСТРОГРАДСКОГО- ГАУССА
- •3.1. Силовые линии
- •Остроградский Михаил Васильевич (1801
- •Гаусс Карл Фридрих (1777 – 1855)
- •силовые линии – это линии, касательная к которым в любой
- •В случае точечного заряда, линии напряженности исходят из положительного заряда и уходят в
- •если на рисунке выделить
- •3.2. Поток вектора
- •Для первого рисунка – поверхность А1 окружает
- •3.3. Теорема Остроградского-
- •поток вектора напряженности через произвольную элементарную площадку dS будет равен:
- •Подсчитаем поток вектора через
- •Центр сферы совпадает с центром
- •Тогда поток через S
- •Из непрерывности линии
- •Для любого числа произвольно
- •Полный поток проходящий через S3, не
- •Таким образом, для точечного заряда q, полный поток через любую
- •Электрические заряды могут быть «размазаны» с некоторой объемной плотностью различной в разных местах
- •Суммарный заряд объема dV будет равен:
- •3.4. Дифференциальная форма теоремы Остроградского-Гаусса
- •Теперь устремим V 0, стягивая его к интересующей нас точке. Очевидно, что при
- •Итак,
- •Сам по себе оператор смысла не
- •3.5.Вычисление электрических полей
- •Представим себе цилиндр с образующими,
- •Суммарный поток через замкнутую поверхность (цилиндр) будет равен: ФЕ 2 SE.
- •3.5.2. Поле двух равномерно заряженных плоскостей
- •Результирующее поле, находится как суперпозиция полей, создаваемых каждой из плоскостей.
- ••Распределение напряженности
- •3.5.3. Поле заряженного бесконечного цилиндра (нити)
- •Представим вокруг цилиндра (нити)
- •Для оснований цилиндров En 0,
- •При r R,на поверхности будет заряд q λl.
- •График
- •3.5.4. Поле двух коаксиальных
- •Внутри меньшего и вне большего цилиндров поле будет отсутствоватьE 0
- •Таким образом для коаксиальных цилиндров
- •3.5.5. Поле заряженного пустотелого шара
- •Вообразим вокруг шара – сферу радиуса r (рис).
- •Если r R,то внутрь воображаемой сферы попадет весь заряд q, распределенный по сфере,
- •Как видно, вне сферы поле
- •3.5.6. Поле объемного заряженного
- •Внутри шара при r R,сферическая
- •Т.е. внутри шара
- •Таким образом, имеем:
- •3.8. Уравнения Пуассона (1812 г) и Лапласа (1782 г).
- •Если между проводниками нет зарядов, т.е. 0 , то уравнение Пуассона переходит в
- •Пример. (Иродов 3.49)
- •Thursday, July 11, 2019

четверг 11 Июль, 2019
ЛЕКЦИЯ 2

Тема 3. ТЕОРЕМА ОСТРОГРАДСКОГО- ГАУССА
3.1. Силовые линии электростатического поля3.2. Поток вектора напряженности3.3. Теорема Остроградского-Гаусса
3.4. Дифференциальная форма теоремы
Остроградского-Гаусса
3
.5. Вычисление электростатических полей с помощью теоремы Остроградского
- Гаусса3.5.1. Поле бесконечной однородно заряженной
плоскости3.5.2. Поле двух равномерно заряженных
плоскостей3.5.3. Поле заряженного бесконечного цилиндра
(нити)
3.5.4. Поле двух коаксиальных цилиндров с
одинаковой линейной плотностью заряда, но разным знаком
3.5.5. Поле заряженного пустотелого шара(сферы)3.5.6. Поле объемного заряженного шара3.6. Уравнения Пуассона и Лапласа.

3.1. Силовые линии
электростатического поля
Теорема Остроградского-Гаусса, которую мы докажем и обсудим позже, устанавливает связь между электрическими зарядами и электрическим полем. Она представляет собой более общую формулировку закона Кулона.
3

Остроградский Михаил Васильевич (1801
– 1862)
отечественный математик и механик. Учился в Харьковском ун-те (1816 – 1820), совершенствовал знания в Париже (1822 – 1827).
Основные работы в области математического анализа, математической физики, теоретической механики. Решил ряд важных задач гидродинамики, теории теплоты, упругости, баллистики, электростатики, в частности задачу распространения волн на поверхности жидкости (1826 г.). Получил дифференциальное уравнение распространения тепла в твердых телах и жидкостях. Известен теоремой Остроградского-Гаусса в электростатике (1828 г.).
4

Гаусс Карл Фридрих (1777 – 1855)
немецкий математик, астроном и физик.
Исследования посвящены многим разделам физики.
В 1832 г. создал абсолютную систему мер (СГС), введя три основных единицы: единицу времени – 1 с, единицу длины – 1 мм, единицу массы – 1 мг.
В 1833 г. совместно с В. Вебером построил первый в Германии электромагнитный телеграф.
Еще в 1845 г. пришел к мысли о конечной скорости распространения электромагнитных взаимодействий. Изу чал земной магнетизм, изобрел в 1837 г. униполярный магнитометр, в 1838 г. – бифилярный. В 1829 г.
Сформулировал принцип наименьшего принуждения (принцип Гаусса).
Один из первых высказал в 1818 г. предположение о возможности существования неевклидовой геометрии.
5
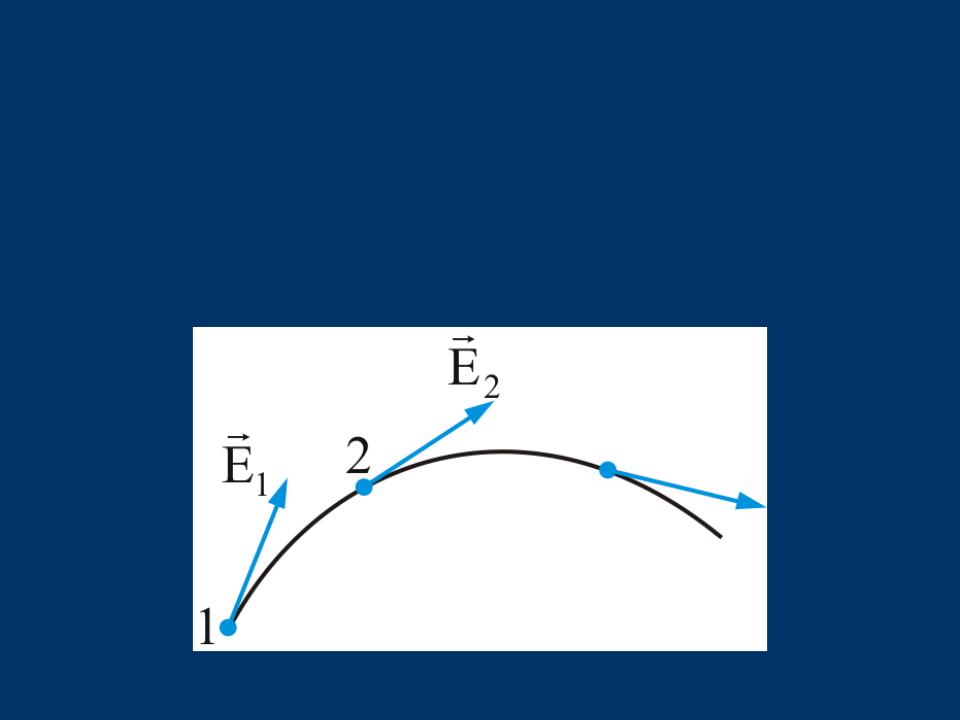
силовые линии – это линии, касательная к которым в любой
точке поля совпадает с направлением вектора
напряженности
6

|
Однородным называется |
|
электростатическое поле, во всех |
|
точках которого напряженность |
|
одинакова по величине и |
|
направлению, т.е. Однородное |
|
электростатическое поле изображается |
|
параллельными силовыми линиями на |
|
равном расстоянии друг от друга |
7

В случае точечного заряда, линии напряженности исходят из положительного заряда и уходят в бесконечность; и из
бесконечности входят в отрицательный заряд. |
|
Т.к. |
Е ~ 1/ r2 , |
то густота силовых линий обратно пропорциональна квадрату расстояния от заряда
8

|
Для системы зарядов, как |
|
видим, силовые линии |
|
направлены от положительного |
|
заряда к отрицательному |
9

10

|
Густота силовых линий должна |
||||
|
быть такой, чтобы единичную |
||||
|
площадку, нормальную к вектору |
||||
|
напряженности пересекало такое |
||||
|
их число, которое равно модулю |
||||
|
вектора напряженности |
|
Е |
|
, т.е. |
|
|
|
|||
|
|
|
|
|
|
|
|
число линий |
Ф . |
|
|||
Е |
|
||
|
|
S |
S |
|
|
11
