Электрический ток при зарядке и разрядке конденсатора.

Рассмотрим процессы зарядки и разрядки конденсаторов в качестве упражнения.

Упражнение 2.

Заряд сферического конденсатора в начальный момент времени равен q₀. Как будет меняться со временем заряд q(t) конденсатора, если между его обкладками находится слабо проводящее вещество с удельной проводимостью и диэлектрической проницаемостью .

Ответ: Изменение заряда со временем q(t) обусловлено его утечкой через проводящую диэлектрическую среду между его обкладками. Ток утечки определяет быстроту изменения заряда и, в свою очередь, определяется разностью потенциалов на обкладках конденсатора. Разность потенциалов определяется зарядом на обкладках по соотношению. Откуда следует:

.

Разделяя переменные, получим дифференциальное соотношение:

,

интегрирование, которого по времени в пределах от дои по заряду в пределах отдоприводит к выражению:

Заметим, что наше рассмотрение носило общий характер и справедливо для описания процесса разрядки любого конденсатора. Для сферического конденсатора , а, гдеи- радиусы внешней и внутренней обкладок конденсатора. Окончательно получим:

Отметим еще раз, что окончательный ответ не зависит от геометрических параметров конденсатора и описывает процесс разрядки произвольного конденсатора с однородными свойствами среды между обкладками.

Упражнение 3.

Конденсатор емкости C  подключили через сопротивление R  к источнику постоянного напряжения U₀. Через сколько времени напряжение на конденсаторе станет U = U₀?

О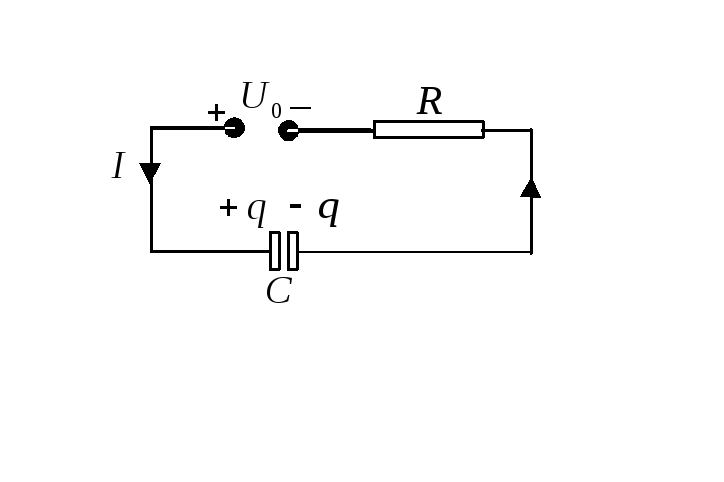твет: Схема процесса зарядки конденсатора от источника напряжения показана на рисунке. Ток зарядки будет увеличивать заряд на обкладках конденсатора по закону. При этом напряжениеравно сумме напряжений на конденсаторе и сопротивлении. Исключая ток из этих выражений, получим зависимость изменения напряжения на конденсаторе в виде:

. Интегрируя методом разделения переменных, получим:

,

Полученный результат, представим в виде:

,

график которого изображен на рисунке.

Время, спустя которое напряжение на конденсаторе станет равным , равно:

.

Упражнение 4.

Покажите, что при зарядке конденсатора через сопротивление от источника с электродвижущей силойполовина работы, совершаемой источником, идет на сообщение энергии конденсатору и половина на нагревание сопротивления.

Ответ: В каждый момент времени процесса зарядки согласно закону Ома для замкнутой цепи ЭДС источника равна сумме падения напряжения на сопротивлении и напряжения на конденсаторе:

,

а мощность источника равна сумме мощности выделения джоулева тепла и мощности, идущей на увеличения энергии конденсатора:

Работа источника по зарядке конденсатора , таким образом, равна сумме выделившегося в процессе зарядки джоулева тепла и энергии заряженного конденсатора

.

Учитывая, что , получим:

9. Электрический ток (примеры решения задач) Сила Тока. Плотность тока

Пример 9.1.

Найдите суммарный импульс электронов в прямом проводе длиной L , по которому течет ток I . Масса электрона m .

Решение.

Суммарный импульс электронов равен импульсу одного электрона умноженному на число электронов в проводе, т.е.. Из определения плотности тока найдем, что, а. Для суммарного импульса получим. Учитывая, что, окончательно получим.

Пример 9.2.

В цилиндрическом проводнике с поперечным сечением радиуса R вектор плотности тока параллелен оси проводника, а его модуль зависит о расстояния r до этой оси по закону , гдеj₀ – известная постоянная. Найдите силу тока в проводнике.

Решение.

Сила тока через элементарную поверхность радиусаи ширины, расположенную в плоскости перпендикулярной оси проводника, равна. Суммируя элементарные токи по всей поверхности поперечного сечения, найдем

.

Пример 9.3.

Металлический шар радиуса a окружен концентрической тонкой металлической оболочкой радиуса b. Пространство между этими электродами заполнено однородной слабо проводящей средой с удельным сопротивлением . Найдите сопротивление межэлектродного промежутка. Рассмотрите случай .

Решение.

Способ 1: Представим, что шар и оболочка заряжены зарядом соответственно. Через слабо проводящую среду, заполняющую пространство между ними, потечет ток разрядки. В силу сферической симметрии распределения зарядов распределение плотности тока будет обладать такой же симметрией, т.е.. Поэтому полный ток утечки через концентрическую сферическую поверхность радиусаравени не зависит от. Напряженность электрического поля в проводящем пространстве будет. Соответствующее напряжение на проводящих обкладках равно:

Для величины , получим. Если проводящая среда занимает все пространство, то ее сопротивление равно.

Способ 2: Представим ток сквозь любуюзамкнутую поверхность окружающую металлический шар как поток поля вектора плотности тока в виде:

,

где - заряд металлического шара (- заряд окружающей сферической оболочки). Разность потенциалов между заряженными поверхностями шара и оболочки равна. Величина сопротивления равная отношению напряжения к току, как и в первом способе решения равна.

Способ 3: Разобьем сферически симметричное пространство проводящей среды на элементарные сферические слои концентрические с металлическими электродами. Сопротивление всей среды при этом разобьется на последовательно соединенные элементарные сопротивления, величина которых равна . Полное сопротивление межэлектродного пространства равно:

.

Пример 9.4.

Два металлических шара одинакового радиуса a находятся в однородной слабо проводящей среде с удельным сопротивлением . Найдите сопротивление среды между шарами при условии, что расстояние между ними значительно больше a.

Решение.

Представим процесс протекания тока между шарами так, как на рисунке. При этом сопротивление всей среды равно последовательно соединенным сопротивлениям, которые получены в предыдущей задаче и равны.

Поэтому полное сопротивление среды .