2. Теорема Гаусса. Использование теоремы Гаусса для расчета полей (Краткая теория, вопросы)

1.Для описания электрического поля как самостоятельного физического объекта наряду с основной характеристикой поля вектора Eвводят скалярную характеристику – поток векторного поля. Потоком поля напряженности через элементарный участок площадиназывают скалярную, алгебраическую величину

гдевектор элементарной площадки с нормалью,θ- угол между векторамии,- проекцияна направление нормали. Знак элементарного потока зависит от выбора направления нормали к поверхности.

Поток напряженности электрического поля через поверхность Sконечного размера определяется как алгебраическая сумма элементарных потоков:

В случае замкнутой поверхности направление нормали выбирается в сторону внешнего пространства. Поток поля напряженности обладает свойством аддитивности, являющимся следствием принципа суперпозиции. Если поле является суперпозицией нескольких полей, то для любой поверхностиSпоток равен, гдеФ_i- поток полячерез поверхность.

Пример 1:

Поток поля напряженности точечного заряда q через площадку ds.

По определению получим:

,

г

де-проекция векторана направление радиус вектора,- телесный угол .Поток через замкнутую поверхность равен,

е

q

сли зарядq находится внутри этой поверхности, и нулю если снаружи.

2. Теорема Гаусса. Поток вектора напряженности электростатического поля через замкнутую поверхность равен алгебраической сумме зарядов внутри поверхности, деленной на.

3.Теорема Гаусса и силовые линии. Для графического представления полей используют силовые линии (линии напряженности ) поля, которые проводятся по следующим правилам:

а) касательная к силовой линии направлена вдоль вектора поля в каждой точке пространства.

б) густота силовых линий пропорциональна напряженности поля в данной точке.

Поток вектора напряженности пропорционален числу силовых линий, пронизывающих поверхность. Теорема Гаусса означает, что силовые линии начинают и заканчиваются на зарядах, а в пустом пространстве непрерывны.

4. Локальная (дифференциальная) форма теоремы Гаусса

Из определения элементарного потока векторного поля следует, что его величина пропорциональна величине площади ds. Замечательным свойством потока вектора через замкнутую поверхность, ограничивающую элементарный объемdV, является пропорциональность потока этому объему. Рассмотрим, например, электростатическое поле. В соответствии с теоремой Гаусса поток полячерез произвольную замкнутую поверхность, а значит и через поверхность, охватывающую элементарный объемdV, определяется величиной заряда, находящегося внутриdV:

Пропорциональность потока величине соответствующего элементарного объема свойственна и другим векторным полям. Этот факт можно представить и на языке линий поля. Действительно, результирующий поток отличен от нуля, если число входящих в замкнутую поверхность линий поля отличается от числа выходящих, т.е. если внутри этой поверхности находятся истоки (откуда исходят линии поля) или стоки (где заканчиваются линии поля). При этом величина потока через замкнутую поверхность пропорциональна полному числу источников и стоков, находящихся внутри поверхности. А так как для физически малого объема dVих число пропорционально самому объемуdV, то и поток через ограничивающую этот объем замкнутую поверхность можно представить в виде:

dF=DdV.

Здесь коэффициент пропорциональности Dхарактеризует плотность пространственного распределения источников поля и называется дивергенцией векторного поля. Для обозначения дивергенции используются следующие символы:

С учетом введенного понятия дивергенции векторного поля теорема Гаусса может быть переписана в виде

Замечание. Однородное векторное полене имеет источников, так как линии такого поля нигде не начинаются и не заканчиваются. Поэтому как поток через произвольную замкнутую поверхность, так и дивергенция этого поля в любой точке равны нулю. Следовательно, отличная от нуля дивергенция характеризует свойства неоднородных векторных полей.

C использованием векторного дифференциального оператора набла

представление дивергенции в декартовых координатах может быть переписано в следующей символической форме:

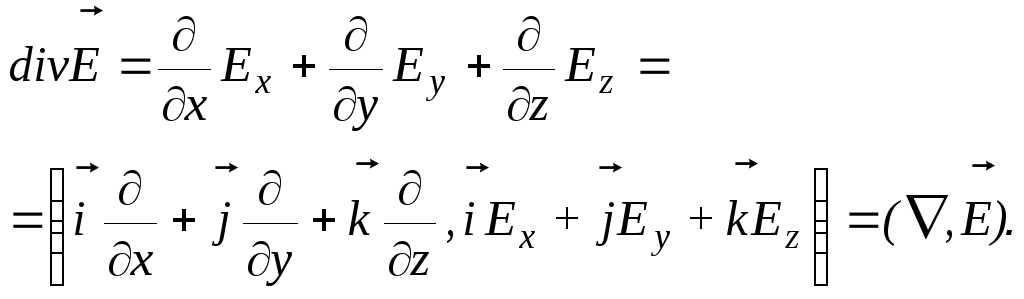
В результате локальная (дифференциальная) теорема Гаусса принимает вид:

Таким образом, хотя величина поля зависит от распределения заряда во всех точках пространства, дивергенция поляв данной точке определяется только плотностью электрического зарядав этой же точке. Это важное и фундаментальное свойство оказывается верным для любых электрических полей. Оператор набла соответствует в векторном анализе операции взятия производной обычного анализа. Действуя оператором набла на скалярные или векторные величины, мы получаем новые величины, имеющие определенный геометрический смысл.

5. Применения теоремы Гаусса.

Если симметрия распределения зарядов позволяет построить замкнутую поверхность (ее называют гауссовой), на части которой векторЕперпендикулярен поверхности и имеет постоянную величинуЕ, а на остальной части поверхности вектор Енаправлен вдоль поверхности, то можно найти величину Е, применив к этой поверхности теорему Гаусса:

,

,

где- заряд внутри гауссовой поверхности.

С помощью локальной формы теоремы Гаусса по заданному электрическому полю всегда можно найти соответствующее распределение электрических зарядов, вычислив дивергенцию данного поля.

Вопросы

2.1 Укажите ошибочные утверждения, относящиеся к формулировке теоремы Гаусса:

а) – алгебраическая сумма зарядов, которые охватываются поверхностью.

б) - электрическое поле, созданное зарядами, расположенными внутри поверхности.

в) – произвольная замкнутая поверхность.

д) теорема Гаусса справедлива только для неподвижных зарядов.

е) теорема Гаусса справедлива только для точечных зарядов.

Ошибочные утверждения:

б)- так как - поле всех зарядов, как внутри, так и снаружи.

д)- так как заряд частицы релятивистки инвариантная величина, не зависит от скорости частицы. Теорема Гаусса справедлива не только для покоящихся, но и для движущихся зарядов.

е)- так как теорема Гаусса справедлива для любого распределения заряда.