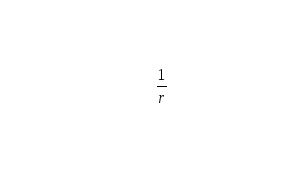Пример 3.5.

Тонкое кольцо радиуса R равномерно заряжено зарядом q. Найдите потенциал электрического поля на оси кольца на расстоянии х от его центра. Воспользовавшись найденной зависимостью , определите напряженность электрического поля на оси кольца. Постройте графики зависимостей потенциала и модуля напряженности электрического поля от координаты х.

Решение.

Электростатическое поле создано зарядом, распределенным по тонкому кольцу заданного радиуса. Для расчета напряженности и потенциала поля будем использовать принцип суперпозиции. Разобьем кольцо на элементарные участки. Каждый участок можно рассматривать как точечный заряд , потенциал создаваемого им поля , где r – расстояние от элемента то точки С (рис.8).

Рис.8

Потенциал результирующего поля получим, проинтегрировав последнее выражение:

.

Из рисунка видно, что . Потенциал электрического поля на оси кольца на расстоянии х от его центра равен:

.

Величина - представляет суммарный заряд кольца. Следовательно, в точках, лежащих на оси кольца, потенциал равен:

.

Воспользовавшись полученной формулой, определим напряженность электрического поля на оси кольца. С учетом симметрии распределения заряда кольца, вектор напряженности в точках оси направлен вдоль самой оси. Проекция вектора напряженности на ось X определится соотношением:

.

Напряженность поля в центре кольца найдем, подставив в полученную формулу x=0:

,

что совпадает с результатом, полученным при решении примеров 1.5 и 1.8, в которых напряженность поля кольца в центре и на его оси была найдена с помощью принципа суперпозиции полей.

Рис.9

Пример 3.6.

Найдите разность потенциалов между центрами двух однородно заряженных сфер зарядами . Радиусы сфер одинаковы и равны, а расстояние между их центрами (рис.11).

Решение.

Рис.11

Воспользовавшись свойством аддитивности потенциала, запишем потенциал в центре первой, а затем в центре второй сферы:

, .

Для искомой разности потенциалов, получим:

.

Пример 3.6.

Круглая тонкая пластинка радиуса однородно заряжена с поверхностной плотностью заряда . Найдите потенциал на оси пластинки как функцию расстояния от ее центра. Рассмотреть случаи и .

Решение.

Мы ранее решили эту задачу для нахождения напряженности с помощью принципа суперпозиции поля. Для нахождения потенциала эта задача решается легче, так как потенциал скалярная функция, а рассуждения аналогичны примеру 1.13. Пусть точка наблюдения находится на оси симметрии пластинки с координатой (рис.12).

Рис.12

Потенциал заряда пластины, удаленного на расстояние r от оси в точке равен:

.

Потенциал зарядов , расположенных на тонком кольце радиуса и ширины , определится суммированием потенциалов отдельных зарядов кольца:

,

где заряд, размещенный на кольце равен:

.

С учетом этого потенциал создаваемый зарядами кольца равен:

,

далее просуммируем потенциалы, создаваемые в точке всеми кольцами, на которые мы разбили пластину

.

Заметим, что в интеграле легко выделить дифференциал от подкоренного выражения знаменателя

Рассмотрим предельные случаи:

1) - потенциал поля однородно заряженной плоскости.

2)

- потенциал поля точечного заряда, помещенного в центр пластинки (использовали приближение малой величины : ).

3) Электрическое поле пластины можно получить, используя связь и

,

что совпадает с результатом, полученным в примере 1.13, в котором напряженность электрического поля на оси круглой однородно заряженной пластинки была получена с помощью принципа суперпозиции.

Пример 3.7.

Найдите потенциал электрического поля сферической поверхности радиуса с зарядом , однородно распределенном по сфере.

Решение.

Так как поле вне сферы совпадает с полем точечного заряда, то поле потенциала сферы в этой области пространства также совпадает с полем потенциала точечного заряда:

, где .

Внутри же сферы напряженность равна нулю, поэтому поле потенциала внутри сферы однородно и в силу непрерывности потенциала равно значению потенциала на поверхности сферы:

.

Пример 3.8

Найдите потенциал электрического поля шара радиуса однородно заряженного по объему зарядом .

Решение. Как и в случае заряженной сферы, поле потенциала вне шара совпадает с полем потенциала точечного заряда:

, где .

Для расчета потенциала точек внутри шара (), используем соотношение:

.

Интегрирование проведем вдоль луча, проходящего через точку наблюдения и центр шара, воспользовавшись выражением для поля внутри шара (см. пример 2.1):

.

Для потенциала в центре шара получим:

.

Для сравнения построим графики зависимости потенциала для различных сферически симметричных распределений заряда рис.13 - поле потенциала точечного заряда; рис.14 - поле потенциала сферы однородно заряженной по поверхности, рис.15 - поле потенциала шара однородно заряженного по объему.

Рис.13.

Рис.14.

Рис.15

51