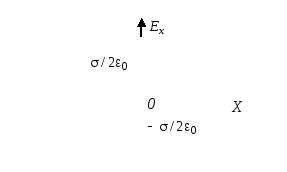3. Потенциал электростатического поля

(теория, вопросы, упражнения)

1. Как и любое стационарное центральное поле, электростатическое поле точечного заряда является потенциальным. Это означает, что работа сил поля при перемещении пробного заряда из одной точки пространства в другую не зависит от траектории. Так как любое электростатическое поле можно представить как суперпозицию полей точечных зарядов, то оно также является потенциальным. Это позволяет выразить работу электрических сил при переносе пробного заряда q через убыль потенциальной энергии заряда во внешнем электростатическом поле:

где - работа сил поля при переносе пробного заряда q из точки в точку, U=. Величина называется разностью потенциалов между точками и. Для однозначного определения потенциала, как и потенциальной энергии надо выбрать точку, где они обращаются в нуль. В СИ потенциал измеряется в вольтах (В).

2. Зная напряженность, можно вычислить разность потенциалов и потенциал по соотношениям:

,

где - точка, в которой потенциал принят равным нулю.

3. Зная потенциал, можно найти проекцию вектора напряженности на любое направление l и сам вектор напряженности по соотношениям:

,

1. Потенциал поля системы зарядов равен сумме потенциалов полей отдельных зарядов в этой точке (принцип аддитивности для потенциала).

Если заряд распределен непрерывно, суммирование надо заменить интегрированием.

5. Геометрическая поверхность, все точки которой имеют одинаковое значение потенциала, называется эквипотенциальной поверхностью. Помещая локальную систему прямоугольных координат с началом на эквипотенциальной поверхности, так чтобы оси X и Y являлись касательными к поверхности, запишем выражение для вектора напряженности:, так как . Направление вектора определяет направление силовых линий, поэтому линии электрического поля нормальны к эквипотенциальным поверхностям и направлены в сторону наиболее резкого уменьшения потенциала.

6. Потенциал поля точечного заряда.

Найдем потенциал точечного заряда, интегрированием напряженности поля вдоль луча выходящего из положения заряда и проходящего через точку, в которой определяется поле:

Обычно, величину потенциала принимают на бесконечности равной нулю. В этом случае:

Упражнение 3.1

Две линии напряженности электрического поля не могут пересекаться в одной точке. Можно ли утверждать, что две эквипотенциальные поверхности также не могут пересекаться в одной точке?

Ответ: Две эквипотенциальные поверхности могут пересекаться в одной точке при условии, что напряженность поля в этой точке равна нулю. В самом деле, вектор напряженности определяет направление нормали к каждой эквипотенциальной поверхности. Так как поверхности пересекаются, в точке пересечения их нормали не совпадают, а значит, электрическое поле не может иметь определенного направления. Это возможно только при нулевом значении величины поля.

Упражнение 3.2

Потенциалы трех близких точек, не лежащих на одной прямой, одинаковы. Что можно сказать о направлении вектора напряженности электрического поля в окрестности этих точек.

Ответ. Проведем через три данные точки элемент поверхности. В силу непрерывности потенциала данный элемент будет принадлежать эквипотенциальной поверхности, а значит, направление вектора напряженности должно быть перпендикулярным к поверхности проходящей через данные точки.

3. Потенциал электростатического поля (примеры решения задач)

Пример 3.1.

Определите потенциал электрического поля бесконечной плоскости, заряженной с поверхностной плотностью . Результат представьте в виде графика зависимости , где ось X имеет начало отсчета (x = 0) на плоскости и перпендикулярна ей. Считайте, что (0) = 0.

Решение.

Согласно результату, полученному при решении примера 2.1 поле напряженности бесконечной плоскости, равномерно заряженной с поверхностной плотностью , определяется соотношением:

.

Разность потенциалов между точками, с координатамии

.

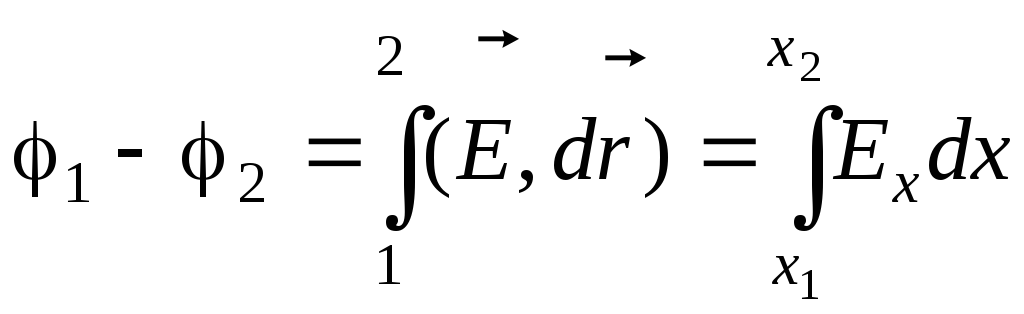Положим , тогда

Графики и показаны на рис.1 и рис.2.

Рис.1	Рис.2

Пример 3.2.

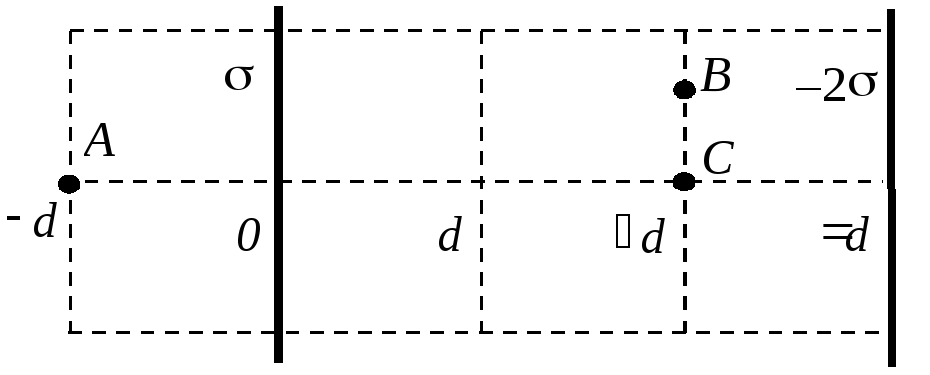Две тонкие параллельные пластины однородно заряжены с поверхностными плотностями и –2. Расстояние между пластинами 3d значительно меньше размеров пластин. Определить разность потенциалов в точках А и В, положение которых указано на рисунке.

Рис.3

Решение.

Согласно решению примера 2.2 напряженность поля заряженных пластин определяется следующим выражением:

.

Разность потенциалов между точками А и В представим в виде

.

Учитывая, что точки В и С принадлежат одной эквипотенциальной поверхности и т.о., найдем разность потенциалов между точками А и В, положение которых согласно рисунку задается координатами :

.

Пример 3.3.

Вычислите потенциал поля заряженной нити

Решение.

Интегрирование напряженности электрического поля для определения потенциала проведем вдоль направления перпендикулярного нити:

Отметим, что никаким выбором постоянной нельзя добиться обращения потенциала в нуль на бесконечности. Это связано с тем, что в рассматриваемом случае на бесконечности имеются не только поля, но и сами заряды. Мы выбрали отсчет потенциала от точки , т.е. выбрали при . График зависимости представлен на рис.4.

Рис.4

Пример 3.4.

Поверхность бесконечно длинного прямого цилиндра радиуса R заряжена однородно поверхностной плотностью . Определите напряженность поля и потенциал внутри и вне поверхности.

Решение.

Сначала определим напряженность электрического поля. Наличие осевой симметрии в распределении заряда, позволяет сделать вывод о том, что вектор в любой точке пространства направлен радиально к оси заряженного цилиндра или от нее, в зависимости от знака заряда. Ввиду той же симметрии величина Е может зависеть только от расстояния до оси:

Е = Е ( r )

Для определения этой зависимости выберем следующую гауссову поверхность. Построим цилиндр высоты l с боковой поверхностью удаленной от оси на расстояние r и основаниями, перпендикулярными к оси симметрии (рис.5). Поток поля вектора через основания цилиндра равен нулю, т.к. . Поток через боковую поверхность равен Е× S , т.к. , S- площадь боковой поверхности.

Рис.5

Из теоремы Гаусса следует:

где - заряд внутри гауссова цилиндра равен:

Подставляя поток и заряды в формульное выражение теоремы Гаусса, получим:

,если ;

, если.

Интегрирование напряженности поля, для определения потенциала вне цилиндра, проведем вдоль направления перпендикулярного к оси цилиндра. Выбрав начало отсчета потенциала на поверхности заряженного цилиндра (т.е. при получим:

Внутри заряженного цилиндра электрическое поле отсутствует, поэтому потенциал во всех точках имеет одно и тоже значение, равное выбранному значению на его поверхности. Графики электрического поля и потенциала представлены на рис.6 и рис.7 соответственно.

Рис.6	Рис.7