Цилиндрический конденсатор

Пример 7.4.

Найдите емкость цилиндрического конденсатора длины l, радиусы обкладок которого a и b, причем a < b, если пространство между обкладками заполнено диэлектриком, проницаемость которого зависит от расстояния r до оси конденсатора как , где.

Решение. Представим цилиндрический конденсатор, как последовательно соединенные элементарные конденсаторы с емкостью . Величина емкости всей системы элементарных конденсаторов найдется из соотношения

. Отсюда окончательно получим ответ:

.

Пример 7.5.

Цилиндрический конденсатор имеет диаметр внешней обкладки .Каким должен быть диаметр внутренней обкладки, чтобы при заданном напряжении на конденсаторенапряженность электрического поля на внутренней обкладкебыла минимальной?

Решение. Величину напряженности электрического поля на внутренней обкладкенайдем из следующих соотношений. Подстановка величины емкости цилиндрического конденсатора (см. упражнение 7.5), приводит к выражению:

.

Для нахождения экстремума найдем производную знаменателя (т.к. величина числителя имеет фиксированное значение)

.

Приравнивая ее нулю, найдем . В том, что это соответствует минимуму, можно убедиться, взяв вторую производную и определив ее знак при.

Соединение конденсаторов

Пример 7.6.

Четыре конденсатора с емкостями исоединены так, как показано на рисунке. Какому соотношению должны удовлетворять емкости конденсаторов, чтобы разность потенциалов между точкамиибыла равна нулю?

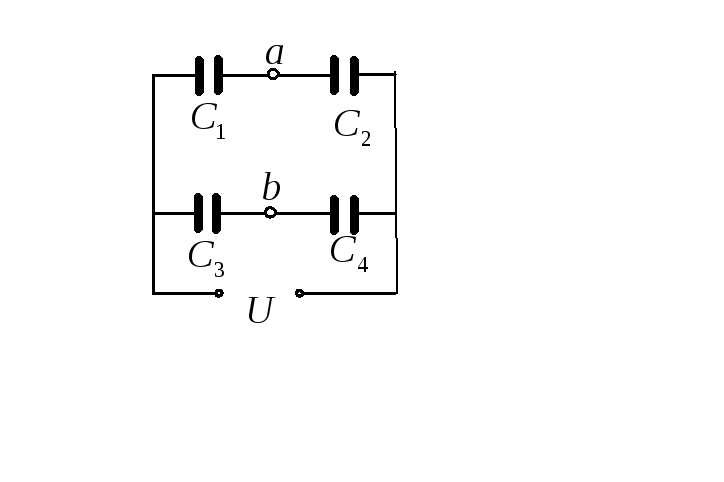
Решение.Так как на последовательно соединенных конденсаторах 1 и 2 заряд одинаков, то выполняется соотношение

.

Аналогичное соотношение должно выполняться для конденсаторов 3 и 4:

.

Для того, чтобы между точками иотсутствовала разность потенциалов, необходимо, чтобы осуществлялись равенстваи. Разделив почленно соотношения выражающие равенства зарядов и сокращая на равные разности потенциалов, получим

. Взаимная емкость

Пример 7.7.

Очень далеко друг от друга находятся два проводника. Емкость одного из них C₁, его заряд Q₁. Емкость второго проводника C₂, заряд Q₂. Первоначально незаряженный конденсатор емкостью С подключают тонкими проводами к этим проводникам. Найдите заряд q конденсатора C.

Решение. После подключения конденсатора и установления электростатического равновесия заряды и потенциалы проводников и обкладок конденсатора будут такими как показано на рисунке. Потенциалы удаленных проводников будут связаны с зарядами на них соотношениями: ,. Для напряжения на конденсаторе запишем соотношение:

,

из которого величина заряда конденсатора может получена алгебраически и представлена в виде:

.

96