5. Проводники в электростатическом поле (краткие теоретические сведения)

Все вещества можно условно разделить на проводники и диэлектрики. В проводниках электрические заряды могут перемещаться из одной точки тела в другую, в диэлектриках такой свободы передвижения у зарядов нет. В обычных условиях тела электрически нейтральны. Положительные заряды атомных ядер скомпенсированы отрицательными зарядами электронов. При внесении тела в электрическое поле (на рис.1 показан проводящий шар в поле точечного заряда) легкие электроны испытывают смещения против поля. Смещения атомных ядер по сравнению с ними пренебрежимо малы. Происходит частичное разделение положительных и отрицательных зарядов. Это явление называется электрической индукцией, а появившиеся в результате разделения заряды – индукционными зарядами.

Индукционные заряды создают дополнительное электрическое поле , которое накладывается на внешнее поле. Внутри проводника полеиндукционных зарядов направлено противоположно внешнему полю, что приводит к ослаблению результирующего электрического поля. Перераспределение носителей заряда в проводнике после «включения» внешнего поля будет происходить до тех пор, пока напряженность полявнутри проводника не станет равной нулю.

Для равновесия зарядов в однородном проводнике необходимо выполнение двух условий:

1) Вектор напряженности электрического поля внутри проводника равен нулю.

2) Вектор напряженности электрического поля вне проводника непосредственно у его поверхности перпендикулярен поверхности проводника.

При нарушении любого из этих условий свободные носители заряда придут в упорядоченное движение в объеме или вдоль поверхности проводника. Равновесие в проводниках устанавливается очень быстро, например, в типичных металлах за время 10^–-14с или менее. После установления равновесия электрическое поле можно считать электростатическим, то есть полем неподвижных зарядов. Далее обсудим некоторые следствия из условий равновесия зарядов в проводнике.

Потенциал во всех точках однородного проводника одинаков. Из условия следует, что разность потенциалов в двух любых точках однородного проводника равна нулю, то есть потенциал всех точек проводника один и тот же. Поэтому можно говорить о потенциалепроводника, не указывая конкретную его точку, в которой определен.

Заряд может располагаться только на поверхности проводника. Если внутри однородного проводника мысленно выбрать любую замкнутую поверхность, то поток вектора напряженностичерез эту поверхность будет равен нулю (так как). Из теоремы Гаусса следует, что суммарный заряд, находящийся внутри этой поверхности, также равен нулю. Поскольку это справедливо для любой замкнутой поверхности, целиком расположенной в проводнике, то можно заключить, что при равновесии заряд может располагаться только на поверхности проводника. Толщина поверхностного слоя, в котором нарушается электрическая нейтральность проводника, настолько мала, что во многих случаях ее можно совсем не принимать во внимание, считая что электрический заряд располагается на поверхности проводника как на геометрической поверхности.

Внутри полости в проводнике напряженность электрического поля равна нулю.Рассмотрим сплошной однородный проводник. Мысленно выделим некоторую замкнутую поверхность внутри этого проводника. Заряд внутри этой поверхности равен нулю. Поэтому, если удалить проводник из области, ограниченной этой поверхностью, то электрическое поле и распределение зарядов на внешней поверхности проводника не изменятся. Следовательно, внутри полости в проводнике полеравно нулю, а заряды располагаются на внешней поверхности проводника. Конечно, это справедливо, если внутри полости отсутствуют заряженные тела.

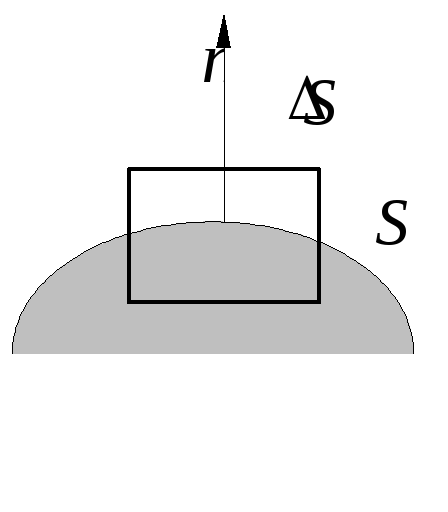
Напряженность поля у поверхности проводникаможно найти при помощи теоремы Гаусса. Рассмотрим поверхность проводникаS, по которой распределены заряды с поверхностной плотностью. Возьмем бесконечно малый прямой цилиндр (малы и его высота и размеры поперечного сечения), основания которого перпендикулярны вектору нормалик поверхности и расположены по разные стороны отS(рис.2). Внутри цилиндра находится электрический заряд, где- площадь основания. Поток векторачерез основание, расположенное в проводнике, равен нулю, так как в проводнике. Поток через верхнее основание, где- проекция вектора напряженности на направление внешней нормали. Поскольку поток через боковую поверхность пренебрежимо мал, то по теореме Гаусса

.

Следовательно, . Учитывая, что вектор напряженности электрического поля на поверхности проводника направлен по нормали к поверхности, можно записать

.

Метод электростатических изображений.Рассмотрим точечный зарядq, расположенный в некоторой точкеAвблизи плоской поверхностиPпротяженного проводника, заполняющего все полупространство (например, правое, см. рис.3). На поверхности проводника возникают индуцированные заряды, распределенные так, что их поле внутри проводника полностью компенсирует поле точечного зарядаq. Следовательно, поле индуцированных зарядов в проводнике равно полю воображаемого заряда –q, помещенногов ту же точку A пространства, что и зарядq. Электрическое поле индуцированных зарядов симметрично относительно плоскостиP. Поэтому в левом полупространстве индуцированные заряды создают такое же поле, что и заряд –q, расположенный симметрично зарядуqотносительно плоскости P (см. рис). Воображаемый заряд –q, полностью заменяющий все наведенные на плоскости заряды, называют изображением зарядаq, а сам метод называют методом электростатических изображений. Согласно этому методу сила притяжения точечного заряда к бесконечной проводящей плоскости равна силе взаимодействия между зарядомqи его «изображением» - зарядом –q:

,

где l– расстояние между зарядомqи плоскостью.