2 семестр МПиТК / 2-й семестр / Лекции Соколова / 2_5

Непрерывность.

Определение 1. Функция непрерывна в точке ,если определена в некоторой и

На языке приращений это будет выглядеть так. Зададим приращение , тогда приращение функции

Если .

Пример. Пусть .

Докажем, что функция непрерывна в любой точке.

Зададим произвольное приращение: , тогда

, теперь если, - функция непрерывна. Из этого и из свойств пределов следует, что всякий многочлен является непрерывной функцией.

Надо сказать о том, что все свойства непрерывных функций сохраняются, так как сохраняются свойства пределов.

Теорема 1. Пусть непрерывна в точке , тогда мы можем рассматривать эту функцию от большего количества переменных, то есть пусть и рассмотрим , тогда - непрерывна в точке.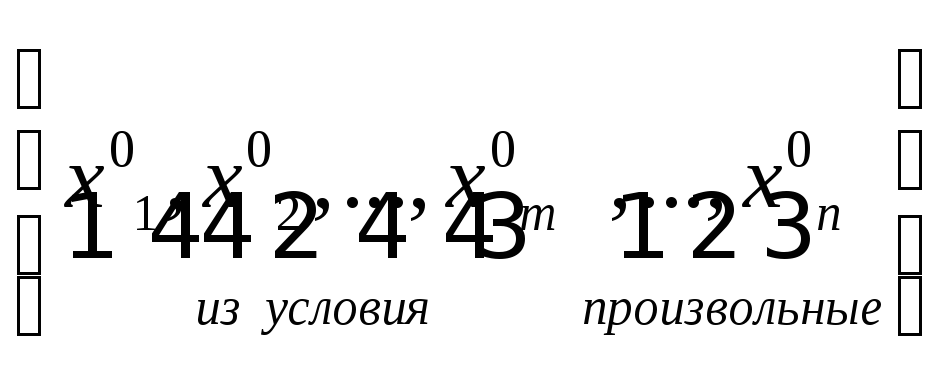

Доказательство:

Приращение новой функции будет равно приращению старой, потому что новая функция от новых переменных не зависит: , то есть . Так как непрерывна, значит и тоже непрерывна.

Если мы теперь рассмотрим произвольную функцию одной переменной и распространим ее на две:

Пример.

В качестве выступает , а мы рассматриваем эту функцию как функцию двух переменных.

Теорема 2. Непрерывность сложной функции.

Пусть непрерывна в точке - мерная точка.

И заданы еще функции.

- -мерная точка и

непрерывны в точке и . То есть, - это фактически функция от . Тогда можно рассмотреть функцию , где . Тогда - непрерывна в точке .

Доказательство:

Так как - непрерывна в точке , то , далее

непрерывна в точке . Возьмем в качестве , чтобы все эти неравенства выполнялись. Мы получаем, что . Это еще немножко не то, там у нас принадлежность шару, но если принадлежит кубу со стороной , то оно принадлежит шару.

Мы получаем, что .

Теорема доказана.

Пример. Введем функцию 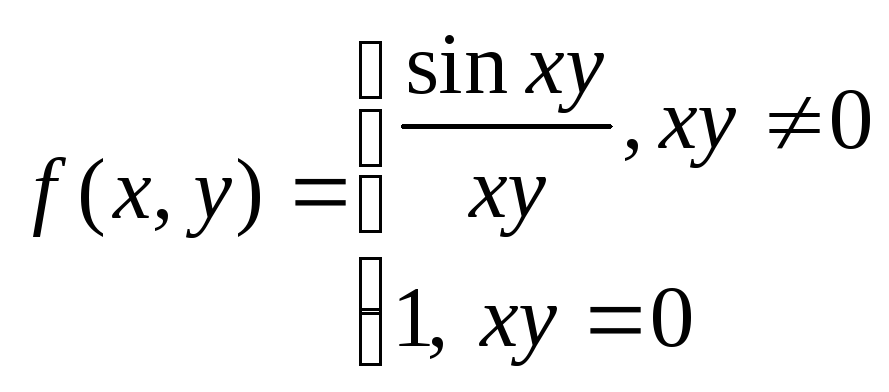. Докажем по этой теореме, что эта функция непрерывна. Рассмотрим 2 функции:

1)- непрерывна .

2)

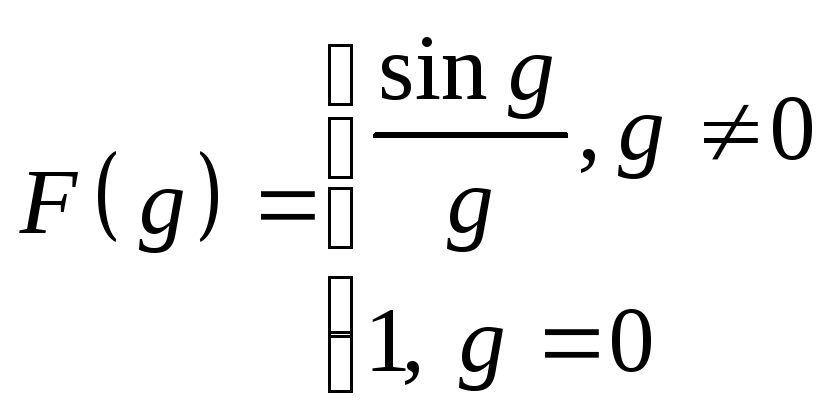
непрерывна . Отсюда следует, что функция тоже непрерывна и ее предел равен 1: .

Непрерывные функции и замкнутые множества.

Мы вводили определение замкнутого множества – это множество, которое содержит все свои предельные точки. Можно переформулировать так: если существует последовательность точек множества, стремящаяся к какой-то точке, то эта точка будет принадлежать множеству.

если , то - замкнутое.

Утверждение. Если непрерывна, то замкнутое, а - открытое.

Доказательство:

Рассмотрим множество и докажем, что оно замкнутое.

Возьмем произвольную последовательность точек , , , тогда нужно доказать, что , по определению замкнутого множества. Это означает, что . Но - непрерывна, переходя к пределу в этом неравенстве, мы получим, что , а этот предел равен (в силу непрерывности). Значит

Для открытых множеств доказать самостоятельно (будет сделано в более поздней версии).

Пример. Теперь доказательство того, что открытый шар – это открытое множество становится совсем простым. Открытый шар: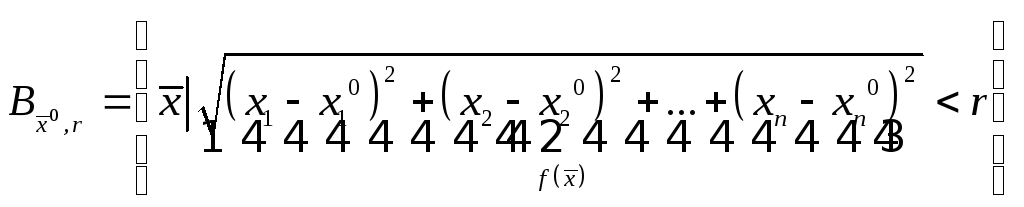, функция является непрерывной. Тогда мы получаем, что это множество является открытым.

Теорема 1. Если - непрерывна на - компакте (замкнутое, ограниченное множество), то ограничена на нем.

Доказательство:

Пусть не ограничена на , тогда .

Множество- ограниченное, следовательно, и последовательность - ограниченная, значит, по теореме Больцано-Вейерштрасса из нее можно извлечь сходящуюся к(в силу замкнутости) подпоследовательность . Мы получаем, что , а , значит в силу непрерывности. Получили с одной стороны больше , а с другой стороны стремится к . Противоречие: не может стремиться к конечному числу, потому что оно больше . Теорема доказана.

Теорема 2. Функция, непрерывная на компакте, достигает своего максимального и минимального значения.

Доказательство:

Рассмотрим множество . Это множество по предыдущей теореме ограниченное, значит, существуют и .

Рассмотрим случай максимума, для минимума все аналогично.

Тогда по определению супремума.

Из последовательности (ограниченной) выделяем сходящуюся,

. Перейдем к пределам, так как непрерывна, получим, что .

Теорема доказана.

Определение 1.

Пусть задана функция , ограниченная на произвольном множестве .

- модуль непрерывности f(x) на множестве А.

- монотонно неубывающая.

Если существует , то - равномерно непрерывная на множестве функция.

Определение 1’. Функция равномерно непрерывна на , если .

Определения 1 и 1’ эквивалентны.

Вспомним разницу между непрерывностью и равномерной непрерывностью. Если мы здесь зафиксируем точку , то получится то же самое, что и для непрерывности. Но, если функция непрерывна, то и найдется , зависящее от и от , такое, что это все будет выполняться. В равномерной непрерывности это существует общее , то есть просто переставлены местами значки существования и всеобщности.

Теорема 3. Функция, непрерывная на компакте, равномерно непрерывна на нем.

Доказательство:

Пусть не равномерно непрерывная на функция, т.е. по второму определению .

Возьмем , тогда

.

принадлежит замкнутому множеству , значит можно из нее извлечь сходящуюся подпоследовательность:

, при .

Рассмотрим последовательность - она тоже ограниченная, и теперь уже из нее извлечем сходящуюся подпоследовательность:

- осталась сходящейся.

Но , далее

, а разность между этими функциями больше , получили противоречие.