
2 семестр МПиТК / 2-й семестр / Лекции Соколова / 2_7
.docВ этом же пункте были заявлены производная по направлению и градиент.
Можно рассматривать производную по направлению как производную сложной функции.
Пусть задана функция
![]() ,
дифференцируемая в точке
,
дифференцируемая в точке
![]() .
.
Рассмотрим направление, единичный
вектор которого имеет координаты
![]() .
.
Рассмотрим производную по этому
направлению, для этого нам нужно
рассмотреть отношение
![]()
Тогда можно рассматривать сложную
функцию переменной
![]()
![]() .
Тогда мы получим, что
.
Тогда мы получим, что
![]()
Мы получаем, что если функция дифференцируема в некоторой точке, то есть имеет непрерывные частные производные, то имеет смысл говорить о производной по произвольному направлению.
Назовем сначала формально ,
а потом докажем, что градиент не зависит
от системы координат.
,
а потом докажем, что градиент не зависит
от системы координат.
Если у нас задан произвольный единичный
вектор
![]()
![]() ,
тогда производная по направлению будет
равна
,
тогда производная по направлению будет
равна
![]() ,
следовательно
,
следовательно
![]() .
.
![]() .
.
Таким образом, градиент
![]() в
точке – это вектор, для которого:
в
точке – это вектор, для которого:
1.![]()
2. Если
![]() ,то
его направление совпадает с направлением,
вдоль которого значение производной
максимально.
,то
его направление совпадает с направлением,
вдоль которого значение производной
максимально.
Докажем теперь, что градиент не зависит от системы координат.
Зададим точку, и направление
![]()
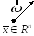
![]() -
не зависит от системы координат,
следовательно, и градиент не зависит
от системы координат.
-
не зависит от системы координат,
следовательно, и градиент не зависит
от системы координат.
Свойства дифференциалов и дифференциалы высших порядков.
Мы доказывали, что если функция
дифференцируема, то она имеет частные
производные. Тогда дифференциал функции
представим в виде
![]() .
.
Тогда у нас сохраняются свойства частных производных, так как частную производную можно рассматривать как производную функции одной переменной. Свойства дифференциала также сохраняются.
1.![]()
2.![]()
3. Если
![]() ,
то
,
то
![]()
Доказательство (3):
 ,
что и требовалось доказать.
,
что и требовалось доказать.
Точно также, как в случае одной переменной определяются дифференциалы высших порядков.
Пусть задана функция
![]() -
дифференцируемая в некоторой точке,
имеющая дифференциал
-
дифференцируемая в некоторой точке,
имеющая дифференциал
![]() ,
в свою очередь этот дифференциал тоже
может быть дифференцируемой функцией.
,
в свою очередь этот дифференциал тоже
может быть дифференцируемой функцией.
![]() .
.
Запишем формулу для дифференциала второго порядка:
![]() .
Возьмем от этого дифференциал
.
Возьмем от этого дифференциал
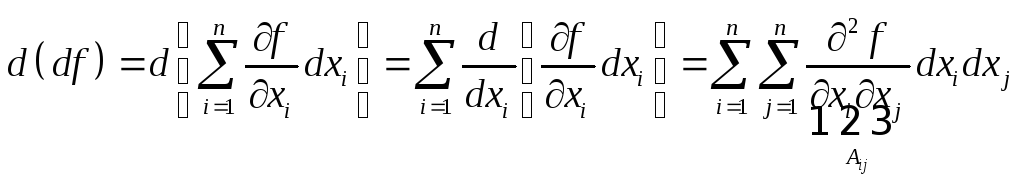
Если функция имеет непрерывные частные производные, то
![]() ,
то есть второй дифференциал представляет
из себя квадратичную форму относительно
дифференциалов независимых переменных.
,
то есть второй дифференциал представляет
из себя квадратичную форму относительно
дифференциалов независимых переменных.
Аналогичным образом можно определить
дифференциал
![]() -го
порядка.
-го
порядка.
![]()
![]()
Инвариантность формы первого дифференциала. Неинвариантность форм высших дифференциалов.
Покажем, что, как и в случае одной переменной, форма первого дифференциала инвариантна, форма высших дифференциалов неинвариантна.
Пусть задана
функция
![]() ,
где
,
где
![]() ,
m-мерная
переменная,
,
m-мерная
переменная,
![]()
![]() ,
где
,
где
![]() ,
n-мерная
переменная, тогда можно рассматривать
функцию
,
n-мерная
переменная, тогда можно рассматривать
функцию
![]() .
.
Предположим, что
всякое
![]() имеет непрерывные частные производные
имеет непрерывные частные производные
![]() ,
и
,
и
![]() имеет непрерывные частные производные
имеет непрерывные частные производные
![]() ,
тогда, учитывая, что
,
тогда, учитывая, что
![]() ,
получим:
,
получим:

т.е. форма первого
дифференциала сохраняется, он выглядит
так же, как если бы
![]() была независимой переменной.
была независимой переменной.
Т.е. форма первого дифференциала инвариантна.
Рассмотрим второй дифференциал при независимой переменной x:
![]()
Пусть теперь
![]() – зависимая переменная:
– зависимая переменная:
![]() ,
,
![]() ,
,![]() .
.
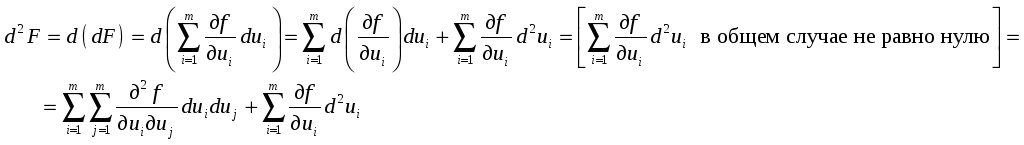
Первая часть
одинакова, независимо от того, зависима
переменная
![]() или нет, а остаток
или нет, а остаток
![]() только в том случае, когда
только в том случае, когда
![]() линейно зависит от x,
т.е.
линейно зависит от x,
т.е.
![]() .
.
Аналогично форма
k-го
дифференциала
![]() инвариантна, когда
инвариантна, когда
![]() - многочлены не выше k-го
порядка от переменных
- многочлены не выше k-го
порядка от переменных
![]() .
.
Формула Тейлора.
Для вывода формулы
Тейлора для функций многих переменных
сведем все к одномерному случаю и
воспользуемся формулой Тейлора для
функций одной переменной с различными
остаточными членами. Пусть задано
связное открытое множество
![]() (связное открытое множество называется
областью). Возьмем произвольную
(связное открытое множество называется
областью). Возьмем произвольную
![]() ,
такую что в этой точке определены и
непрерывны все частные производные до
k-го
порядка:
,
такую что в этой точке определены и
непрерывны все частные производные до
k-го
порядка:
![]() . Тогда эти частные производные определены
в некоторой окрестности
. Тогда эти частные производные определены
в некоторой окрестности
![]() (вследствие их непрерывности). Возьмем
точку
(вследствие их непрерывности). Возьмем
точку
![]() ,
тогда все точки вида
,
тогда все точки вида
![]() ,
если
,
если![]() .
Тогда зададим функцию
.
Тогда зададим функцию
![]() ,
t
– переменная:
,
t
– переменная:
![]() ,
она определена при
,
она определена при
![]() .
.
Заметим, что
![]() ,
,
![]() .
.
Наша задача состоит
в том, чтобы представить значение функции
в точке
![]() с помощью значений функции и ее частных
производных в точке
с помощью значений функции и ее частных
производных в точке
![]() .
Т.е. нам нужно значение функции
.
Т.е. нам нужно значение функции
![]() представить с помощью значений функции
и ее частных производных при
представить с помощью значений функции
и ее частных производных при
![]() .
Запишем формулу Тейлора для функции
.
Запишем формулу Тейлора для функции
![]() с остаточным членом в форме Лагранжа в
окрестности точки
с остаточным членом в форме Лагранжа в
окрестности точки
![]() :
:
![]()
![]()
Найдем
![]() как производную сложной функции многих
переменных:
как производную сложной функции многих
переменных:
![]() ,
тогда
,
тогда
![]() .
.
Рассчитаем
![]() опять же как производную сложной функции
многих переменных:
опять же как производную сложной функции
многих переменных:
![]()
Теперь запишем остаточный член второго порядка в форме Лагранжа.
 Обозначим
через
Обозначим
через
![]() - длина вектора и подставим все полученные
выражения в формулу Тейлора с остаточным
членом в форме Лагранжа:
- длина вектора и подставим все полученные
выражения в формулу Тейлора с остаточным
членом в форме Лагранжа:
![]() ,
подставим
,
подставим
![]() ,
получим
,
получим
![]()

Докажем, что
![]() ,
т.е. получим остаточный член в форме
Пеано:
,
т.е. получим остаточный член в форме
Пеано:
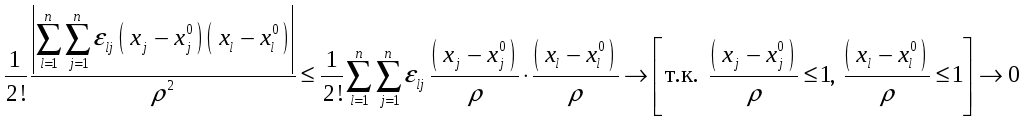
Теперь мы можем записать формулу Тейлора и с остаточным членом в форме Пеано:
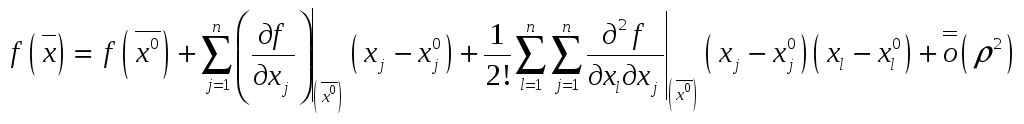
или для разложения до k-го порядка:
![]() ,
где
,
где
![]() - дифференциал функции, вычисленный в
точке
- дифференциал функции, вычисленный в
точке
![]() на приращении
на приращении
![]() .
.
Пример:
Разложим функцию
![]() по формуле Тейлора в окрестности точки
по формуле Тейлора в окрестности точки
![]() до второго порядка.
до второго порядка.
![]()
![]()
![]()
![]()
![]()
То же самое мы бы получили, если бы разложили по формуле Тейлора в случае одной переменной каждый из множителей:
![]()
Если мы это перемножим, то получится то же самое, если мы загоним все большие степени в о-малое.
