1 семестр МП / Экзамен 2 поток / Осевые моменты инерции некоторых тел

Осевые моменты инерции некоторых тел

Моменты инерции однородных тел простейшей формы относительно некоторых осей вращения
Тело	Описание	Положение оси a	Момент инерции Ja
	Материальная точка массы m	На расстоянии r от точки, неподвижная
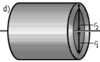
	Полый тонкостенный цилиндр или кольцо радиуса r и массы m	Ось цилиндра
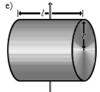
	Сплошной цилиндр или диск радиуса r и массы m	Ось цилиндра
	Полый толстостенный цилиндр массы m с внешним радиусом r2 и внутренним радиусом r1	Ось цилиндра
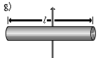
	Сплошной цилиндр длины l, радиуса r и массы m	Ось перпендикулярна к цилиндру и проходит через его центр масс
	Полый тонкостенный цилиндр (кольцо) длины l, радиуса r и массы m	Ось перпендикулярна к цилиндру и проходит через его центр масс
	Прямой тонкий стержень длины l и массы m	Ось перпендикулярна к стержню и проходит через его центр масс
	Тонкостенная сфера радиуса r и массы m	Ось проходит через центр сферы
	Шар радиуса r и массы m	Ось проходит через центр шара
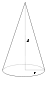
	Конус радиуса r и массы m	Ось конуса
	Равнобедренный треугольник с высотой h, основанием a и массой m	Ось перпендикулярна плоскости треугольника и проходит через вершину
	Правильный треугольник со стороной a и массой m	Ось перпендикулярна плоскости треугольника и проходит через центр масс
	Квадрат со стороной a и массой m	Ось перпендикулярна плоскости квадрата и проходит через центр масс

Вывод формул

Тонкостенный цилиндр (кольцо, обруч)

Момент инерции тела равен сумме моментов инерции составляющих его частей. Разобъём тонкостенный цилиндр на элементы с массой dm и моментами инерции dJ_i. Тогда

Поскольку все элементы тонкостенного цилиндра находятся на одинаковом расстоянии от оси вращения, формула (1) преобразуется к виду

Толстостенный цилиндр (кольцо, обруч)

Пусть имеется однородное кольцо с внешним радиусом R, внутренним радиусом R₁, толщиной h и плотностью ρ. Разобьём его на тонкие кольца толщиной dr. Масса и момент инерции тонкого кольца радиуса r составит

Момент инерции толстого кольца найдём как интеграл

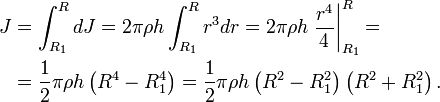
Поскольку объём и масса кольца равны

получаем окончательную формулу для момента инерции кольца

Однородный диск (сплошной цилиндр)

Рассматривая цилиндр (диск) как кольцо с нулевым внутренним радиусом (R₁ = 0), получим формулу для момента инерции цилиндра (диска):

Сплошной конус

Разобьём конус на тонкие диски толщиной dh, перепендикулярные оси конуса. Радиус такого диска равен

где R – радиус основания конуса, H – высота конуса, h – расстояние от вершины конуса до диска. Масса и момент инерции такого диска составят

Интегрируя, получим

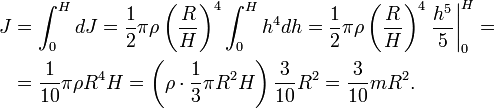
Сплошной однородный шар

Разобъём шар на тонкие диски толщиной dh, перпендикулярные оси вращения. Радиус такого диска, расположенного на высоте h от центра сферы, найдём по формуле

Масса и момент инерции такого диска составят

Момент инерции сферы найдём интегрированием:

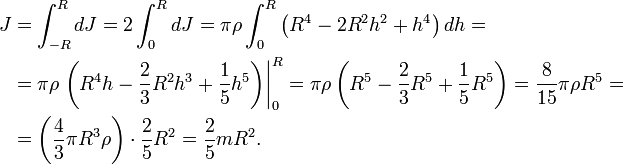
Тонкостенная сфера

Для вывода воспользуемся формулой момента инерции однородного шара радиуса R:

Вычислим, насколько изменится момент инерции шара, если при неизменной плотности ρ его радиус увеличится на бесконечно малую величину dR.

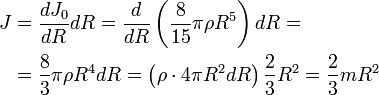
Тонкий стержень (ось проходит через центр)

Разобъём стержень на малые фрагменты длиной dr. Масса и момент инерции такого фрагмента равна

Интегрируя, получим

Тонкий стержень (ось проходит через конец)

При перемещении оси вращения из середины стержня на его конец, центр тяжести стержня перемещается относительно оси на расстояние l/2. По теореме Штейнера новый момент инерции будет равен